2、（97年全国理）如果函数对任意实数都有，那么（      ）

    A、                      B、

    C、                          D、

    1、（94年上海）设I是全集，集合P、Q满足，则下面的结论中错误的是（   ）

    A、    B、     C、     D、

Q：不等式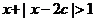的解集为R，如果P和Q有且仅有一个正确，求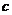的取值范围.

P：函数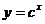在R上单调递减.

已知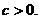  设

33．（2003年（19）.12分）

32.已知函数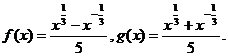(2003年春上海(20)7＋7＝14分)
(1) 证明f(x)是奇函数；并求f(x)的单调区间；
(2) 分别计算f(4)－5f(2)g(2)和f(9)－5f(3)g(3)的值，由此概括出涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式，并加以证明.

31.某租赁公司拥有汽车100辆. 当每辆车的月租金为3000元时，可全部租出. 当每辆车的月租金每增加50元时，未租出的车将会增加一辆. 租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元.(2003年春北京(20)12分)
   (Ⅰ)当每辆车的月租金定为3600元时，能租出多少辆车？
   (Ⅱ)当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？

30.设a为实数，函数f(x)＝x²＋|x－a|－1，x∈R(2002年全国(21)12分)
(1)讨论f(x)函数的奇偶性
(2)求函数f(x)的最小值.

29.已知a＞0，函数f(x)＝ax－bx²(2002年广东(22)14分)
(1)当b＞0时，若对任意x∈R都有f(x)≤1，证明：a≤2；
(2)当b＞1时，证明：对任意x∈[0，1]，|f(x)|≤1的充要条件是b－1≤a≤2；
(3)当0＜b≤1时，讨论：对任意x∈[0，1]，|f(x)|≤1的充要条件.