
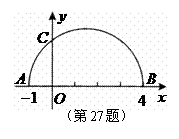
 (4)设点
(4)设点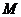 是抛物线上任意一点,过点
是抛物线上任意一点,过点 作
作 轴,交
轴,交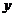 轴于点
轴于点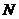 .若在线段
.若在线段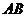 上有且只有一点
上有且只有一点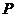 ,使
,使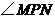 为直角,求点
为直角,求点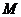 的坐标.
的坐标.
(3)在(2)的条件下,若在抛物线上有一点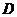 ,使四边形
,使四边形 为直角梯形,求直线
为直角梯形,求直线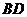 的解析式;
的解析式;
(2)求过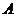 ,
,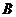 ,
,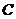 三点的抛物线的解析式;
三点的抛物线的解析式;
(1)求点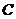 的坐标;
的坐标;
27.(14分)如图所示,在平面直角坐标系中有点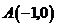 ,点
,点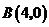 ,以
,以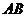 为直径的半圆交
为直径的半圆交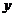 轴正半轴于点
轴正半轴于点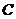 .
.
 (3)利用图中已标明的字母,连结线段,找出至少
(3)利用图中已标明的字母,连结线段,找出至少 对相似三角形(不包含全等,不需要证明).多写者给附加分,附加分不超过3分,计入总分,但总分不超过120分.
对相似三角形(不包含全等,不需要证明).多写者给附加分,附加分不超过3分,计入总分,但总分不超过120分.
六、综合题(本题14分)
(2)在切线 上截取
上截取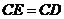 ,连结
,连结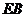 ,判断直线
,判断直线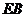 与
与 的位置关系,并证明;
的位置关系,并证明;
(1)求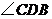 的度数;
的度数;
26.(12分)已知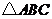 内接于以
内接于以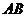 为直径的
为直径的 ,过点
,过点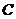 作
作 的切线交
的切线交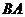 的延长线于点
的延长线于点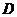 ,且
,且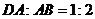 .
.
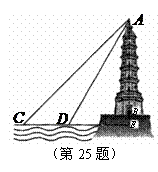 25.(9分)某中学初三(2)班数学活动小组利用周日开展课外实践活动,他们要在湖面上测量建在地面上某塔
25.(9分)某中学初三(2)班数学活动小组利用周日开展课外实践活动,他们要在湖面上测量建在地面上某塔 的高度.如图,在湖面上点
的高度.如图,在湖面上点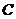 测得塔顶
测得塔顶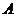 的仰角为
的仰角为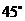 ,沿直线
,沿直线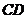 向塔
向塔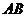 方向前进
方向前进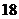 米到达点
米到达点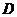 ,测得塔顶
,测得塔顶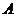 的仰角为
的仰角为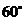 .已知湖面低于地平面
.已知湖面低于地平面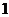 米,请你帮他们计算出塔
米,请你帮他们计算出塔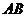 的高度(结果保留根号).
的高度(结果保留根号).
五、证明题(本题12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com