附加题：在第26题中，抛物线的解析式和点D的坐标不变(如图14)．当x > 0时，在直线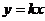(0 < k < 1)和这条抛物线上，是否分别存在点P和点Q，使四边形DOPQ为以OD为底的等腰梯形．若存在，求点P、Q的坐标；若不存在，说明理由．

26．如图13，直线AB交x轴于点A(2，0)，交抛物线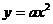于点B(1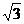，)，点C到△OAB各顶点的距离相等，直线AC交y轴于点D．当x > 0时，在直线OC和抛物线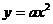上是否分别存在点P和点Q，使四边形DOPQ为特殊的梯形？若存在，求点P、Q的坐标；若不存在，说明理由．

25．两个全等的Rt△ABC和Rt△EDA如图12放置，点B、A、D在同一直线上．

操作：在图12中，作∠ABC的平分线BF，过点D作DF⊥BF，垂足为F，连结CE．

探究：线段BF、CE的关系，并证明你的结论．

说明：如果你无法证明探究所得的结论，可以将“两个全等的Rt△ABC和Rt△EDA”改为“两个全等的等腰直角△ABC和等腰直角△EDA(点C、A、E在同一直线上)”，其他条件不变，完成你的证明，此证明过程最多得2分．

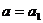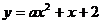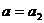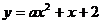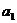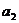⑶当时，抛物线与x轴的正半轴相交于点M(m，0)；当时，抛物线与x轴的正半轴交于点N(n，0)．若点M在点N的左边，试比较与的大小．

⑵若代数式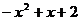的值为正整数，求x的值；

24．已知抛物线 ．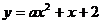

⑴当a =－1时，求此抛物线的顶点坐标和对称轴；

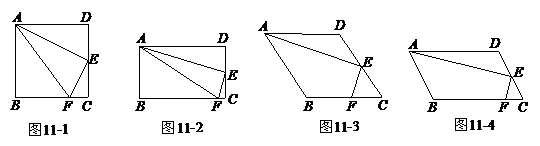
五、解答题和附加题(本题共3小题，24、25题各12分，26题10分，共34分，附加题5分，全卷累积不超过150分，建议考生最后答附加题)