
科目: 来源:2017年海南省定安县中考数学仿真试卷(三) 题型:填空题
方程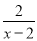 ﹣
﹣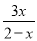 =1的解是_____.
=1的解是_____.
查看答案和解析>>
科目: 来源:2017年海南省定安县中考数学仿真试卷(三) 题型:填空题
如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)_____________.
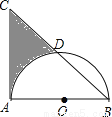
查看答案和解析>>
科目: 来源:2017年海南省定安县中考数学仿真试卷(三) 题型:填空题
如图,将矩形纸片ABCD沿AE折叠,使点B落在对角线AC上的点F处,再沿EG折叠,使点C落在矩形内的点H处,且E、F、H在同一直线上,若AB=6,BC=8,则CG的长是_____.
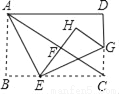
查看答案和解析>>
科目: 来源:2017年海南省定安县中考数学仿真试卷(三) 题型:解答题
(1)计算:﹣13+20170×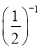 ﹣
﹣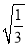 ×
×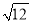 ;
;
(2)解不等式组:  .
.
查看答案和解析>>
科目: 来源:2017年海南省定安县中考数学仿真试卷(三) 题型:解答题
食品安全关乎民生,食品中添加过量的添加剂对人体有害,但适量的添加剂对人体无害且有利于食品的储存.某饮料厂为了解A、B两种饮料添加剂的添加情况,随机抽检了A种30瓶,B种70瓶,检测发现,A种每瓶比B种每瓶少1克添加剂,两种共加入了添加剂270克,求A、B两种饮料每瓶各加入添加剂多少克?
A种饮料每瓶加入添加剂2克,B种饮料每瓶加入添加剂3克. 【解析】试题分析:设种饮料每瓶加入添加剂克, 种饮料每瓶加入添加剂克,根据种每瓶比种每瓶少1克添加剂结合30瓶种饮料70瓶种饮料共加入了添加剂270克,即可得出关于的二元一次方程组,解之即可得出结论. 试题解析:设种饮料每瓶加入添加剂克, 种饮料每瓶加入添加剂克, 根据题意得: 解得: 答:A种饮料每瓶加入添加...查看答案和解析>>
科目: 来源:2017年海南省定安县中考数学仿真试卷(三) 题型:解答题
为了解某种新能源汽车的性能,对这种汽车进行了抽检,将一次充电后行驶的里程数分为A,B,C,D四个等级,其中相应等级的里程依次为200千米,210千米,220千米,230千米,获得如下不完整的统计图.请根据图中提供的信息,解答下列问题:
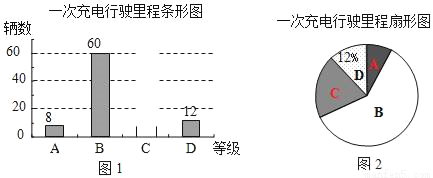
(1)这次被抽检的新能源汽车共有 辆;
(2)将图1补充完整;在图2中,C等级所占的圆心角是 度;
(3)估计这种新能源汽车一次充电后行驶的平均里程数为多少千米?(精确到千米)
(1)100;(2)72;(3)估计这种新能源汽车一次充电后行驶的平均里程数为214千米. 【解析】试题分析:(1)利用D等级的数量和它所占的百分比可计算出抽检的电动汽车的总数; (2)用C等级所占的百分比乘以360°可得C等级对应的扇形的圆心角; (3)根据题意列式计算即可. 试题解析:(1)12÷12%=100, 答:这次被抽检的新能源汽车共有100辆; 故答案为:...查看答案和解析>>
科目: 来源:2017年海南省定安县中考数学仿真试卷(三) 题型:解答题
A、B两市相距150千米,分别从A、B处测得国家级风景区中心C处的方位角如图所示,风景区区域是以C为圆心,45千米为半径的圆,tanα=1.627,tanβ=1.373.为了开发旅游,有关部门设计修建连接AB两市的高速公路.问连接AB高速公路是否穿过风景区,请说明理由.
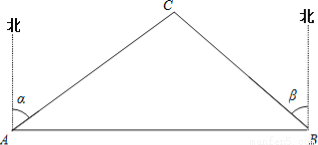
查看答案和解析>>
科目: 来源:2017年海南省定安县中考数学仿真试卷(三) 题型:解答题
如图,把两个边长相等的等边△ABC和△ACD拼成菱形ABCD,点E、F分别是射线CB、DC上的动点(E、F与B、C、D不重合),且始终保持BE=CF,连结AE、AF、EF.
(1)求证:①△ABE≌△ACF;②△AEF是等边三角形;
(2)①当点E运动到什么位置时,EF⊥DC?
②若AB=4,当∠EAB=15°时,求△CEF的面积.
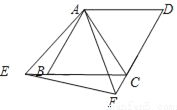
查看答案和解析>>
科目: 来源:2017年海南省定安县中考数学仿真试卷(三) 题型:解答题
如图1,二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于点C.若tan∠ABC=3,一元二次方程ax2+bx+c=0的两根为﹣8、2.
(1)求二次函数的解析式;
(2)直线l绕点A以AB为起始位置顺时针旋转到AC位置停止,l与线段BC交于点D,P是AD的中点.
①求点P的运动路程;
②如图2,过点D作DE垂直x轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在l运动过程中,∠EPF的大小是否改变?请说明理由;
(3)在(2)的条件下,连结EF,求△PEF周长的最小值.
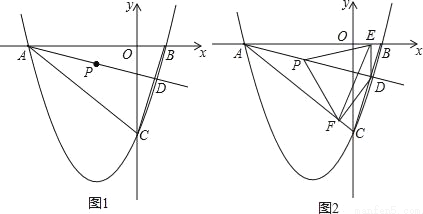
查看答案和解析>>
科目: 来源:山东省2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com