
科目: 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:填空题
已知圆锥的底面半径为1cm,母线长为3cm,则其全面积为________cm2 .
【答案】4π
【解析】试题解析:底面圆的半径为1cm,则底面周长=2πcm,底面积是πcm2 .
侧面面积=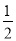 ×2π×3=3πcm2 .
×2π×3=3πcm2 .
则全面积=3π+π=4πcm2 .
点睛:圆锥的侧面积=底面周长×母线长÷2.
【题型】填空题
【结束】
12
已知扇形的圆心角为60°,半径为2,则扇形的弧长为________(结果保留π).
【解析】试题解析:依题意,n=60,r=2, ∴扇形的弧长= .查看答案和解析>>
科目: 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:填空题
已知扇形的圆心角为60°,半径为2,则扇形的弧长为________(结果保留π).
【答案】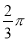
【解析】试题解析:依题意,n=60,r=2,
∴扇形的弧长= 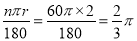 .
.
【题型】填空题
【结束】
13
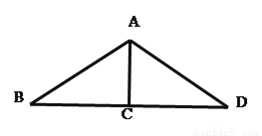
如图,在△ABC中,∠BAC=90°,AD⊥BC于D,BD=3,CD=12,则AD的长为________
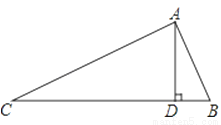
查看答案和解析>>
科目: 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:填空题
如图,在△ABC中,∠BAC=90°,AD⊥BC于D,BD=3,CD=12,则AD的长为________
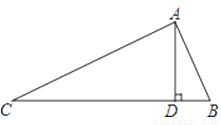
【答案】6
【解析】试题分析:根据射影定理得到AD2=CD•BD,代入计算即可得到答案.
【解析】
∵∠BAC=90°,AD⊥BC,
∴AD2=CD•BD=36,
∴AD=6,
故答案为:6.
考点:射影定理.
【题型】填空题
【结束】
14
已知点A(3,﹣6)是二次函数y=ax2上的一点,则这二次函数的解析式是 .
y=﹣x2 【解析】 试题分析:将点A(3,﹣6)代入y=ax2,利用待定系数法法求该二次函数的解析式即可得﹣6=9a, 解得a=﹣;因此该二次函数的解析式为:y=﹣x2.查看答案和解析>>
科目: 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:填空题
已知点A(3,﹣6)是二次函数y=ax2上的一点,则这二次函数的解析式是 .
【答案】y=﹣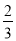 x2
x2
【解析】
试题分析:将点A(3,﹣6)代入y=ax2,利用待定系数法法求该二次函数的解析式即可得﹣6=9a,
解得a=﹣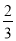 ;因此该二次函数的解析式为:y=﹣
;因此该二次函数的解析式为:y=﹣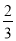 x2.
x2.
考点:待定系数法求二次函数解析式
【题型】填空题
【结束】
15
在一个不透明的口袋中装有8个红球和若干个白球,它们除颜色外其它完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在40%附近,则口袋中白球可能有________个.
12 【解析】试题解析:设口袋中白球可能有x个, ∵摸到红球的频率稳定在40%附近, ∴口袋中摸到红色球的概率为40%, ∴=40%, 解得:x=12, 故答案为12.查看答案和解析>>
科目: 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:填空题
在一个不透明的口袋中装有8个红球和若干个白球,它们除颜色外其它完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在40%附近,则口袋中白球可能有________个.
【答案】12
【解析】试题解析:设口袋中白球可能有x个,
∵摸到红球的频率稳定在40%附近,
∴口袋中摸到红色球的概率为40%,
∴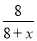 =40%,
=40%,
解得:x=12,
故答案为12.
【题型】填空题
【结束】
16
在等腰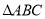 中,当顶角A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也确定了,我们把这个比值记作T(A),即
中,当顶角A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也确定了,我们把这个比值记作T(A),即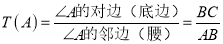 .例:T(60
.例:T(60 )=1,那么T(120
)=1,那么T(120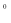 )=____________ ;
)=____________ ;
查看答案和解析>>
科目: 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:填空题
在等腰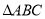 中,当顶角A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也确定了,我们把这个比值记作T(A),即
中,当顶角A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也确定了,我们把这个比值记作T(A),即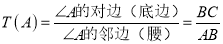 .例:T(60
.例:T(60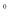 )=1,那么T(120
)=1,那么T(120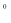 )=____________ ;
)=____________ ;
【答案】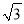
【解析】作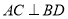 ,垂足为C.
,垂足为C.
设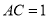
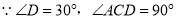
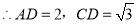
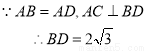
则T(120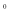 )=
)=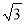
【题型】填空题
【结束】
17
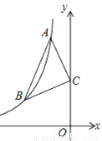
如图:已知点A、B是反比例函数y=﹣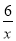 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
查看答案和解析>>
科目: 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:填空题
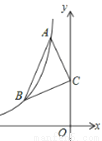
如图:已知点A、B是反比例函数y=﹣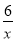 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
【答案】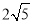
【解析】过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,过点A作AF⊥BE轴于点F,如图所示.
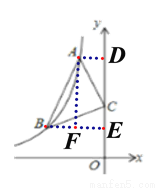
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
又∵AD⊥y轴,BE⊥y轴,
∴∠ACD+∠CAD=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,∠BCE=∠CAD.
在△ACD和△CBE中,由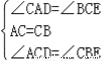 ,
,
∴△ACD≌△CBE(ASA).
设点B的坐标为(m,﹣ )(m<0),则E(0,﹣
)(m<0),则E(0,﹣ ),点D(0,3﹣m),点A(﹣
),点D(0,3﹣m),点A(﹣ ﹣3,3﹣m),
﹣3,3﹣m),
∵点A(﹣ ﹣3,3﹣m)在反比例函数y=﹣
﹣3,3﹣m)在反比例函数y=﹣ 上,
上,
 ,解得:m=﹣3,m=2(舍去).
,解得:m=﹣3,m=2(舍去).
∴点A的坐标为(﹣1,6),点B的坐标为(﹣3,2),点F的坐标为(﹣1,2),
∴BF=2,AF=4,
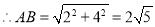
故答案为:2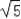 .
.
【点睛】
过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,过点A作AF⊥BE轴于点F,根据角的计算得出“∠ACD=∠CBE,∠BCE=∠CAD”,由此证出△ACD≌△CBE;再设点B的坐标为(m,﹣ ),由三角形全等找出点A的坐标,将点A的坐标代入到反比例函数解析式中求出m的值,将m的值代入A,B点坐标即可得出点A,B的坐标,并结合点A,B的坐标求出点F的坐标,利用勾股定理即可得出结论.
),由三角形全等找出点A的坐标,将点A的坐标代入到反比例函数解析式中求出m的值,将m的值代入A,B点坐标即可得出点A,B的坐标,并结合点A,B的坐标求出点F的坐标,利用勾股定理即可得出结论.
【题型】填空题
【结束】
18
二次函数y=x2+(2m+1)x+(m2﹣1)有最小值﹣2,则m=________.
【解析】试题解析:∵二次函数有最小值﹣2, ∴y=﹣, 解得:m=.查看答案和解析>>
科目: 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:解答题
二次函数y=x2+(2m+1)x+(m2﹣1)有最小值﹣2,则m=________.
【答案】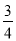
【解析】试题解析:∵二次函数有最小值﹣2,
∴y=﹣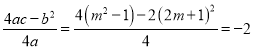 ,
,
解得:m=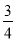 .
.
【题型】填空题
【结束】
19
如图,已知△ABC三个顶点的坐标分别是A(-2,3),B(-3,-1),C(-1,1)
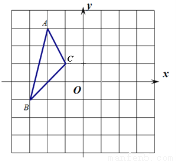
(1)画出△ABC绕点O逆时针旋转90°后的△A1B1C1,并写出点A1的坐标;
(2)画出△ABC绕点O逆时针旋转180°后的△A2B2C2,并写出点A2的坐标;
(3)直接回答:∠AOB与∠A2OB2有什么关系?
(1)作图见解析,(-4,-2);(2)作图见解析,(2,-3);(3)相等. 【解析】 试题分析:(1)根据旋转的性质作图,写出点的坐标; 根据旋转的性质作图,写出点的坐标; (3)根据旋转的性质得出结论. 试题解析:(1)作图如下,点A1的坐标(-4,-2). (2)作图如下,点A2的坐标(2,-3). (3)相等.查看答案和解析>>
科目: 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:解答题
如图,已知△ABC三个顶点的坐标分别是A(-2,3),B(-3,-1),C(-1,1)
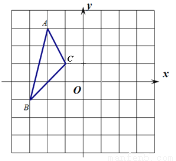
(1)画出△ABC绕点O逆时针旋转90°后的△A1B1C1,并写出点A1的坐标;
(2)画出△ABC绕点O逆时针旋转180°后的△A2B2C2,并写出点A2的坐标;
(3)直接回答:∠AOB与∠A2OB2有什么关系?
【答案】(1)作图见解析,(-4,-2);(2)作图见解析,(2,-3);(3)相等.
【解析】
试题分析:(1)根据旋转的性质作图,写出点的坐标;
根据旋转的性质作图,写出点的坐标;
(3)根据旋转的性质得出结论.
试题解析:(1)作图如下,点A1的坐标(-4,-2).
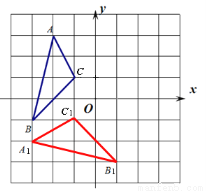
(2)作图如下,点A2的坐标(2,-3).
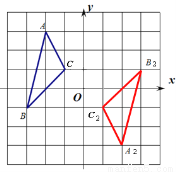
(3)相等.
考点:1.旋转作图;2.旋转的性质.
【题型】解答题
【结束】
20
已知函数y=(m﹣2)xm2+m-4 +2x﹣1是一个二次函数,求该二次函数的解析式.
y=﹣5x2+2x﹣1 【解析】试题分析:根据二次函数的定义得到m2+m﹣4=2且m﹣2≠0,由此求得m的值,进而得到该二次函数的解析式. 试题解析:依题意得:m2+m﹣4=2且m﹣2≠0. 即(m﹣2)(m+3)=0且m﹣2≠0, 解得m=﹣3, 则该二次函数的解析式为y=﹣5x2+2x﹣1查看答案和解析>>
科目: 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:解答题
已知函数y=(m﹣2)xm2+m-4 +2x﹣1是一个二次函数,求该二次函数的解析式.
【答案】y=﹣5x2+2x﹣1
【解析】试题分析:根据二次函数的定义得到m2+m﹣4=2且m﹣2≠0,由此求得m的值,进而得到该二次函数的解析式.
试题解析:依题意得:m2+m﹣4=2且m﹣2≠0. 即(m﹣2)(m+3)=0且m﹣2≠0,
解得m=﹣3,
则该二次函数的解析式为y=﹣5x2+2x﹣1
【题型】解答题
【结束】
21
如图,在?ABCD中,EF∥AB,FG∥ED,DE:DA=2:5,EF=4,求线段CG的长.
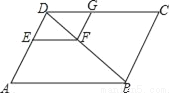
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com