
科目: 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:填空题
反比例函数y=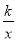 在第一象限的图象如图,请写出一个满足条件的k值,k=__________.
在第一象限的图象如图,请写出一个满足条件的k值,k=__________.
查看答案和解析>>
科目: 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:填空题
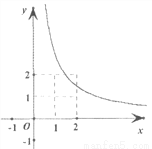
“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,城墙CD长9里,城墙BC长7里,东门所在的点E,南门所在的点F分别是CD,BC的中点,EG⊥CD,EG=15里,FH⊥BC,点C在HG上,问FH等于多少里?答案是FH=________里.
查看答案和解析>>
科目: 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:填空题
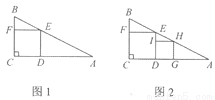
我们定义:“四个顶点都在三角形边上的正方形是三角形的内接正方形”.已知:在Rt△ABC中,∠C=90°,AC=6,BC=3.
(1)如图l,四边形CDEF是△ABC的内接正方形,则正方形CDEF的边长a1是________;
(2)如图2,四边形DGHI是(1)中△EDA的内接正方形,那么第2个正方形DGHI的边长记为a2;继续在图2中的△HGA中按上述方法作第3个内接正方形……以此类推,则第n个内接正方形的边长an=____. (n为正整数)
查看答案和解析>>
科目: 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:解答题
已知二次函数y=x2-2x-3.
(1)求出这个函数图象的对称轴和顶点坐标:
(2)求出这个函数图象与x轴、y轴的交点坐标.
(1)对称轴是x=1,顶点坐标是(1,-4); (2)图象与x轴交点坐标是(-l,0)、(3,0),与y轴的交点坐标是(0,-3) 【解析】试题分析:(1)利用配方法整理到顶点式即可得; (2)分别令x=0、y=0,解方程即可得. 试题解析:(1)∵y=x2-2x-3=(x-1)2-4, ∴对称轴是x=1,顶点坐标是(1,-4); (2)令y=0,则x2-2x-...查看答案和解析>>
科目: 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:解答题
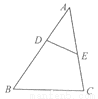
如图,△ABC中,D、E分别是AB、AC上的点,且满足AB·AD=AE·AC,连接DE. 求证:∠ABC=∠AED.
查看答案和解析>>
科目: 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:解答题
若二次函数y=x2+bx+c的图象经过点(0,1)和(1,-2)两点,求此二次函数的表达式.
二次函数的表达式为y=x2-4x+1. 【解析】试题分析:把点(0,1)和(1,-2)分别代入二次函数的解析式,利用待定系数法进行求解即可得. 试题解析:∵二次函数y=x2+bx+c的图象经过(0,1)和(1,-2)两点, ∴ 解得 ∴二次函数的表达式为y=x2-4x+1.查看答案和解析>>
科目: 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:解答题
如图,在矩形ABCD中,E为AD边上的一点,过C点作CF⊥CE交AB的延长线于点F.
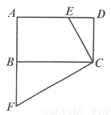
(1)求证:△CDE∽△CBF;
(2)若B为AF的中点,CB=3,DE=1,求CD的长.
(1)证明见解析;(2)CD= 【解析】试题分析:(1)如图,通过证明∠D=∠1,∠2=∠4即可得; (2)由△CDE∽△CBF,可得CD:CB=DE:BF,根据B为AF中点,可得CD=BF,再根据CB=3,DE=1即可求得. 试题解析:(1)∵四边形ABCD是矩形, ∴∠D=∠1=∠2+∠3=90° , ∵CF⊥CE, ∴∠4+∠3=90°, ∴∠2=∠...查看答案和解析>>
科目: 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:解答题
抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y,的对应值如下表:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | -4 | -4 | 0 | 8 | … |
(1)根据上表填空:
①抛物线与x轴的交点坐标是_________和_________;
②抛物线经过点(-3,_________);
(2)试确定抛物线y=ax2+bx+c的解析式.
(1)①(-2,0),(1,0);②8;(2)所求抛物线解析式为y=2x2+2x-4. 【解析】试题分析: (1)①根据表格中函数值y=0即可得到与x轴的交点坐标; ②观察表格可知抛物线的对称轴为x=,由此可知(2,8)与(-3,8)关于对称轴对称,从而可得; (2)依题意设抛物线解析式为y=a(x+2)(x-1),代入点(0,-4)即可求得. 试题解析:(1)①观察表格可...查看答案和解析>>
科目: 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:解答题
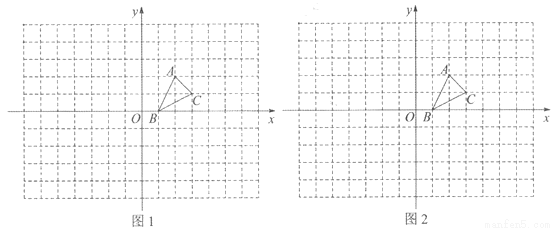
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)
(1)在图l中画出△ABC关于x轴对称的△A1B1C1;
(2)在图2中,以点O为位似中心,将△ABC放大,使放大后的△A2B2C2与△ABC的对应边的比为2:1(画出一种即可). 直接写出点A的对应点A2的坐标.
查看答案和解析>>
科目: 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:解答题
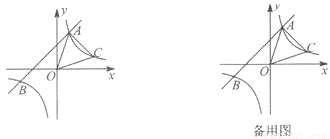
已知:如图,一次函数y=x+2的图象与反比例函数y=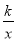 的图象交于A、B两点,且点A的坐标为(1,m).
的图象交于A、B两点,且点A的坐标为(1,m).
(1)求反比例函数y=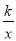 的表达式;
的表达式;
(2)点C(n,1)在反比例函数y=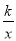 的图象上,求△AOC的面积.
的图象上,求△AOC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com