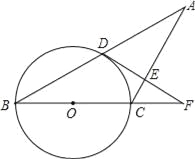
已知：如图，△ABC中，AC=BC，以BC为直径的⊙O交AB于点D，过点D作DE⊥AC于点E，交BC的延长线于点F．

求证：

（1）AD=BD；

（2）DF是⊙O的切线．

（1）证法一：连结CD， ∵BC为⊙O的直径 ∴CD⊥AB ∵AC＝BC ∴AD＝BD． 证法二：连结CD， ∵BC为⊙O的直径 ∴∠ADC＝∠BDC＝90° ∵AC＝BC，CD＝CD ∴△ACD≌△BCD ∴AD＝BD （2）证法一：连结OD， ∵AD＝BD，OB＝OC ∴OD∥AC ∵DE⊥AC ∴DF⊥...

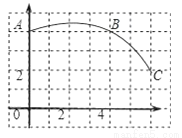
如图，在正方形网格图中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格中进行下列操作：

（1）请在图中确定该圆弧所在圆心D点的位置，D点坐标为　 　；

（2）连接AD、CD，求⊙D的半径及扇形DAC的圆心角度数；

（3）若扇形DAC是某一个圆锥的侧面展开图，求该圆锥的底面半径．

D（2，0） 【解析】（1）找到AB，BC的垂直平分线的交点即为圆心坐标； （2）利用勾股定理可求得圆的半径；易得△AOD≌△DEC，那么∠OAD=∠CDE，即可得到圆心角的度数为90°； （3）求得弧长，除以2π即为圆锥的底面半径． 【解析】 （1）如图；D（2，0） （2）如图；AD===2； 作CE⊥x轴，垂足为E． ∵△AOD≌△DEC， ∴∠OA...

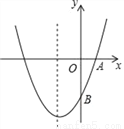
如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣1，且经A（1，0）、

B（0，﹣3）两点．（1）求抛物线的解析式；

（2）在抛物线的对称轴x=﹣1上，是否存在点M，使它到点A的距离与到点B的距离之和最小，如果存在求出点M的坐标，如果不存在请说明理由．

(1) y=x2+2x﹣3；(2) 存在,理由见解析. 【解析】试题分析：（1）利用待定系数法即可求得函数的解析式； （2）抛物线与x轴的除A外的另一个交点C就是A的对称点，则BC与对称轴的交点就是M，首先求得C的坐标，然后求得BC的解析式，进而求得M的坐标． 试题解析：【解析】 （1）根据题意得： ，解得： ，则二次函数的解析式是y=x2+2x﹣3； （2）存在．设抛物...

某商场销售一种成本为每件30元的商品，销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似看作一次函数y＝－10x＋600，商场销售该商品每月获得利润为w（元）．

（1）求w与x之间的函数关系式；

（2）如果商场销售该商品每月想要获得2000元的利润，那么每月成本至少多少元？

（3）为了保护环境，政府部门要求用更加环保的新产品替代该商品，商场销售新产品，每月的销量与销售价格之间的关系与原产品的销售情况相同，新产品的成本每件32元，若新产品每月的销售量不低于200件时，政府部门给予每件4元的补贴，试求定价多少元时，每月销售新产品的利润最大？求出最大的利润。

（1）w＝－10x2＋900x－18000; (2) 3000元; (3) 40元，最大利润为2400元. 【解析】试题分析：（1）根据：月利润=（销售单价﹣成本价）×销售量，从而列出关系式； （2）令w=2000，然后解一元二次方程，从而求出销售单价，再根据：月成本=成本价×销售量可得答案； （3）根据销售量低于200件和不低于200件求出x的范围，并根据：利润=每件产品的利润...

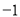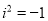定义：如果一个数的平方等于，记为，这个数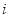叫做虚数单位．那么和我们所学的实数对应起来就叫做复数，表示为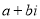（为实数），叫这个复数的实部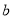， 叫做这个复数的虚部，它的加，减，乘法运算与整式的加，减，乘法运算类似．

例如计算：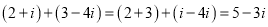

（1）填空： =_________， =____________．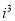

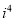（2）填空：①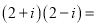_________； ②_________ ．

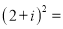（3）若两个复数相等，则它们的实部和虚部必须分别相等，完成下列问题：已知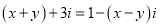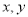， ，（ 为实数），求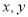的值．

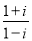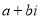（4）试一试：请利用以前学习的有关知识将化简成的形式．

（5）解方程：x2 - 2x +4 = 0

（1） -I，1；（2）5，3+4i ；（3）x=-1，y=2；（4） i ；（5）x1= i ，x2= i 【解析】试题分析：（1）根据同底数幂的乘法法则、i2=﹣1计算即可； （2）利用平方差公式、完全平方公式把原式展开，根据i2=﹣1计算即可； （3）根据复数相等的条件解答即可； （4）充分利用i2=﹣1计算，分子分母同时乘以（1+i）即可； （5）计算出△=－...

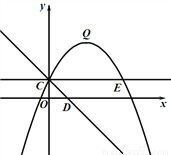
如图，抛物线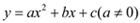的图象过点C（0，1），顶点为Q（2，3）,点D在x轴正半轴上，线段OD=OC.

（1）求抛物线的解析式；

（2）抛物线上是否存在点M，使得△CDM是以CD为直角边的直角三角形？若存在，请求出M点的坐标；若不存在，请说明理由；

（3）将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E，连接QE.若点P是线段QE上的动点，点F是线段OD上的动点，问：在P点和F点的移动过程中，△PCF的周长是否存在最小值？若存在，求出这个最小值，若不存在，请说明理由.

（1） ；（2）(2 , 3 )或 )或；（3）存在， . 【解析】试题分析： （1）根据已知条件设抛物线解析式为，代入点C的坐标就可以求出解析式了； （2）①当点C是直角顶点时，由已知求出直线DM的解析式，再把所求解析式和（1）中所求二次函数解析式组合成方程组，解方程组即可求得点M的坐标；②当点D是直角顶点时，同①的方法可求得对应的M的坐标； （3）如图3，分别作点C关于...

下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是

A. B. C. D.

B 【解析】A、不是轴对称图形，不符合题意；B、是轴对称图形，符合题意；C、不是轴对称图形，不符合题意；D、不是轴对称图形，不符合题意， 故选B．

下列四组线段中，可以组成三角形的是

A. 1，2，3 B. 2，3，4 C. 4，4，8 D. 3，4，9

B 【解析】A、∵1+2=3，∴不能组成三角形，故A选项错误；B、∵2+3>4，∴能组成三角形，故B选项正确；C、∵4+4=8，∴不能组成三角形，故C选项错误；D、∵4+3<9，∴不能组成三角形，故D选项错误， 故选B．

在一个直角三角形中，有一个锐角等于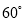，则另一个锐角的度数是

A. 75° B. 60° C. 45° D. 30°

D 【解析】∵在一个直角三角形中，有一个锐角等于60°， ∴另一个锐角的度数是90°-60°=30°， 故选D．

点关于x轴的对称点的坐标是

A. （3 , 2） B. （—3,2） C. （—3, —2） D. （3, —2）

D 【解析】关于x轴对称的点，横坐标相同，纵坐标互为相反数，所以点P(3，2)关于x轴的对称点的坐标是(3，-2)， 故选D．