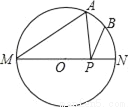
如图，MN是⊙O的直径，MN=2a，∠AMN=40°，点B为弧AN的中点，点P是直径MN上的一个动点，则 PA+PB的最小值为_____．（用含a的代数式表示）

a 【解析】作B点关于MN的对称点B′，连接AB′交MN于P，如图， 则PB=PB′， ∴PA+PB=PA+PB′=AB′， ∴此时PA+PB的值最小， ∵∠AMN=40°， ∴∠AON=80°， ∵点B为弧AN的中点， ∴∠BON=∠AON=40°， ∵B点关于MN的对称点B′， ∴∠B′ON=40°， ∴∠AOB′=120°， ...

解方程：x2﹣2x=0．

x1=0，x2=2 【解析】试题分析：先用因式分解法将方程变形为x(x-2)=0,求解等价方程x=0、x-2=0,即可得到原方程的解. 试题解析：x（x﹣2）=0， x=0或x﹣2=0， 所以x1=0，x2=2.

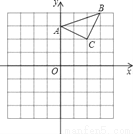
已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．

（1）以点B为位似中心，在网格内画出△A1B1C1，使△A1B1C1与△ABC位似，且位似比为2：1．

（2）点C1的坐标为（　 　，　 　）．

(1)见解析；（2）(1,0) 【解析】试题分析：延长BA到A1，使BA1=2BA，则点A1为点A的对应点，同样方法得到C点的对应点C1，点B1与B点重合，则可得到△A1B1C1； （2）由（1）中的图形即可写出点C1的坐标. 试题解析：（1）如图，△A1B1C1为所作； （2）由图可得，C1点的坐标为（1，0）． 故答案为：（1，0）．

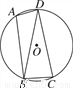
如图，已知四边形ABCD内接于圆O，连接BD，∠BAD＝105°，∠DBC＝75°.

(1)求证：BD＝CD；

(2)若圆O的半径为3，求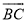的长．

（1）证明见解析；（2）π. 【解析】试题分析： 根据圆内接四边形的对角互补，∠DCB＋∠BAD＝180°，即可求出 的度数，得出，根据等角对等边即可证明. 求出的度数，根据弧长公式计算即可. 试题解析： 证明：∵四边形ABCD内接于圆O， ∴∠DCB＋∠BAD＝180°. ∵∠BAD＝105°， ∴∠DCB＝180°－105°＝75°. ∵∠...

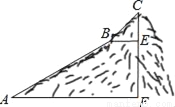
如图，为测量一座山峰CF的高度，将此山的某侧山坡划分为AB和BC两段，每一段山坡近似是“直”的，测得坡长AB=800米，BC=200米，坡角∠BAF=30°，∠CBE=45°．

（1）求AB段山坡的高度EF；

（2）求山峰的高度CF（结果保留根式）．

(1) 400米；(2) （100+400）米 【解析】（1）作BH⊥AF于H，如图，在Rt△ABF中根据正弦的定义可计算出BH的长，从而得到EF的长； （2）先在Rt△CBE中利用∠CBE的正弦计算出CE，然后计算CE和EF的和即可． 试题解析：（1）作BH⊥AF于H，如图， 在Rt△ABH中，∵sin∠BAH=， ∴BH=800•sin30°=400， ∴E...

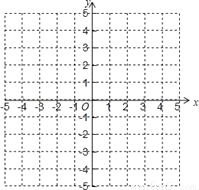
已知二次函数y=﹣x2+2x+3．

（1）画出这个函数的图象；

（2）根据图象，直接写出；

①当函数值y为正数时，自变量x的取值范围；

②当﹣2＜x＜2时，函数值y的取值范围．

(1)见解析；（2）①﹣1＜x＜3；②﹣5＜y＜4． 【解析】试题分析：（1）把二次函数的一般式转化成顶点式即可求得顶点坐标；根据5点画出函数的图象； （2）①根据函数的图象即可求得；②根据函数的图象即可求得. 试题解析：（1）∵y=﹣x2+2x+3=﹣（x﹣1）2+4， ∴函数图象的顶点坐标（1，4）； 函数的图象如图： （2）根据图象可知： ①函数值y...

甲、乙两个不透明的口袋，甲口袋中装有3个分别标有数字1，2，3的小球，乙口袋中装有2个分别标有数字4，5的小球，它们的形状、大小完全相同，现随机从甲口袋中摸出一个小球记下数字，再从乙口袋中摸出一个小球记下数字．

（1）请用列表或树状图的方法（只选其中一种），表示出两次所得数字可能出现的所有结果；

（2）求出两个数字之和能被3整除的概率．

（1）树状图见解析；（2）. 【解析】试题分析：先根据题意画树状图，再根据所得结果计算两个数字之和能被3整除的概率． 试题解析：（1）树状图如下： （2）∵共6种情况，两个数字之和能被3整除的情况数有2种， ∴两个数字之和能被3整除的概率为， 即P（两个数字之和能被3整除）=．

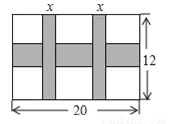
（2016内蒙古包头市）一幅长20cm、宽12cm的图案，如图，其中有一横两竖的彩条，横、竖彩条的宽度比为3：2．设竖彩条的宽度为xcm，图案中三条彩条所占面积为ycm2．

（1）求y与x之间的函数关系式；

（2）若图案中三条彩条所占面积是图案面积的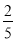，求横、竖彩条的宽度．

（1）；（2）横彩条的宽度为3cm，竖彩条的宽度为2cm． 【解析】试题分析：（1）由横、竖彩条的宽度比为3：2知横彩条的宽度为xcm，根据“三条彩条面积=横彩条面积+2条竖彩条面积﹣横竖彩条重叠矩形的面积”，列出函数关系式化简即可；（2）根据“三条彩条所占面积是图案面积的”，可列出关于x的一元二次方程，整理后求解即可． 试题解析：（1）根据题意可知，横彩条的宽度为xcm， ∴y...

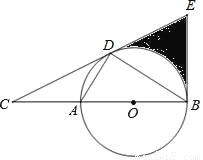
如图，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD．

（1）求证：CD是⊙O的切线；

（2）过点B作⊙O的切线交CD的延长线于点E，CD=2．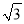

①若∠C=30°，求图中阴影部分的面积；

②若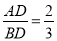，求BE的长．

(1)证明见解析；（2）①4- ；②。 【解析】试题分析：（1）首先连接OD，由AB是直径，可得∠ADB=90°，然后由∠CDA=∠CBD，求得∠CDO=90°，即可证得结论； （2）①由∠CBD=30°，可得△ADO是边长为1的等边三角形，继而求得CD的长，然后由S阴影=S四边形OBED﹣S扇形OBD求得答案；②由∠C=∠C，∠CDA=∠CBD，可证得△CDA∽△CBD，可得比例式=...

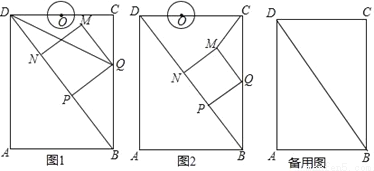
如图，在矩形ABCD中，AB=6cm，AD=8cm，点P从点B出发，沿对角线BD向点D匀速运动，速度为4cm/s，过点P作PQ⊥BD交BC于点Q，以PQ为一边作正方形PQMN，使得点N落在射线PD上．点O从点D出发，沿DC向点C匀速运动，速度为3cm/s，以O为圆心，1cm半径作⊙O．点P与点D同时出发，设它们的运动时间为t（单位：s） （0≤t≤）．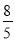

（1）如图1，连接DQ，若DQ平分∠BDC，则t的值为　 　s；

（2）如图2，连接CM，设△CMQ的面积为S，求S关于t的函数关系式；

（3）在运动过程中，当t为何值时，⊙O与MN第一次相切？

（1）1s; （2）S=﹣t2+t；（3）. 【解析】试题分析：（1）由△DQC≌△DQP，推出DP=DC=6，在Rt△ADB中，BD=10，推出PB=4即可解决问题； （2）过点M作MH⊥BC于点H，证明△HMQ∽△PQB，，由=，得MH=t，即可求得△CMQ的面积； （3）设⊙O与MN相切于点E，连接OE，作OF⊥BD于点F，可证得△DFO∽△DCB， 由此即可解得：t...