
科目: 来源:北师大版七年级数学下2.1.2 垂线的定义与性质 同步练习 题型:单选题
已知在同一平面内:①两条直线相交成直角;②两条直线互相垂直;③一条直线是另一条直线的垂线.那么下列因果关系:①→②③;②→①③;③→①②中,正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
D 【解析】垂直的定义:再同一平面内,两条直线相交成直角时,称这两条直线互相垂直,其中一条直线是另一条直线的垂线.由此可知三种因果关系都正确. 故选:D.查看答案和解析>>
科目: 来源:北师大版七年级数学下2.1.2 垂线的定义与性质 同步练习 题型:单选题
下列选项中,过点P画AB的垂线,三角板放法正确的是( )
A. 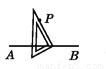
B. 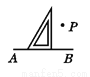
C. 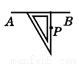
D. 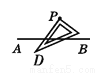
查看答案和解析>>
科目: 来源:北师大版七年级数学下2.1.2 垂线的定义与性质 同步练习 题型:单选题
过一条线段外一点,作这条线段的垂线,垂足在( )
A. 这条线段上 B. 这条线段的端点处
C. 这条线段的延长线上 D. 以上都有可能
D 【解析】作一条线段的垂线,实际上是作线段所在直线的垂线,垂足可能在这条线段上,可能在端点处,也可能在线段的延长线上.查看答案和解析>>
科目: 来源:北师大版七年级数学下2.1.2 垂线的定义与性质 同步练习 题型:单选题
下列说法正确的有( )
①在同一平面内,过直线上一点有且只有一条直线垂直于已知直线;
②在同一平面内,过直线外一点有且只有一条直线垂直于已知直线;
③在同一平面内,过一点可以画一条直线垂直于已知直线;
④在同一平面内,有且只有一条直线垂直于已知直线.
A. 1个 B. 2个 C. 3个 D. 4个
C 【解析】试题解析:由垂线的性质可知①②③正确. 故选C.查看答案和解析>>
科目: 来源:北师大版七年级数学下2.1.2 垂线的定义与性质 同步练习 题型:单选题
如图,过点P作直线l的垂线和斜线,叙述正确的是( )
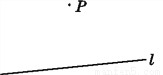
A. 都能作且只能作一条
B. 垂线能作且只能作一条,斜线可作无数条
C. 垂线能作两条,斜线可作无数条
D. 均可作无数条
B 【解析】∵过一点有且只有一条直线与已知直线垂直;而过一点可以做无数条斜线. 故选:B.查看答案和解析>>
科目: 来源:北师大版七年级数学下2.1.2 垂线的定义与性质 同步练习 题型:单选题
如图,如果直线ON⊥直线a,直线OM⊥直线a,那么OM与ON重合(即O,M,N三点共线),其理由是( )
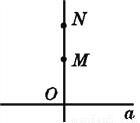
A. 过两点只有一条直线
B. 在同一平面内,过两点有且只有一条直线与已知直线垂直
C. 在同一平面内,过一点有且只有一条直线与已知直线垂直
D. 两点之间,线段最短
C 【解析】因为OM⊥直线a,ON⊥直线a,所以直线ON与OM重合, 其理由是:过一点有且只有一条直线垂直于已知直线. 故选:C.查看答案和解析>>
科目: 来源:北师大版七年级数学下2.1.2 垂线的定义与性质 同步练习 题型:解答题
(1)在图①中,过AB外一点M作AB的垂线;
(2)在图②中,分别过A,B作OB,OA的垂线.
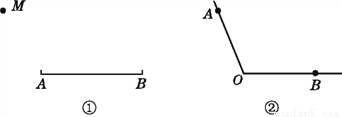
查看答案和解析>>
科目: 来源:北师大版七年级数学下2.1.2 垂线的定义与性质 同步练习 题型:解答题
在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是多少?
120° 【解析】试题分析:需要分类讨论,C,D在AB同侧,∠AOC+∠COD+∠DOB=180°,易得∠BOD;C,D在AB异侧,∠COA+∠AOD=90°,∠AOD+∠BOD=180°,可得∠BOD. 试题解析: 【解析】 (1)如图,当OC,OD在AB一侧时, ∵OC⊥OD,∴∠COD=90°. ∵∠AOC=30°,∴∠BOD=180°-∠COD-∠AOC=6...查看答案和解析>>
科目: 来源:北师大版七年级数学下2.1.2 垂线的定义与性质 同步练习 题型:解答题
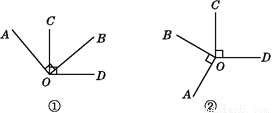
已知OA⊥OB,OC⊥OD.
(1)如图①,若∠BOC=50°,求∠AOD的度数.
(2)如图②,若∠BOC=60°,求∠AOD的度数.
(3)根据(1)(2)结果猜想∠AOD与∠BOC有怎样的关系?并根据图①说明理由.
(4)如图②,若∠BOC∶∠AOD=7∶29,求∠COB和∠AOD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com