
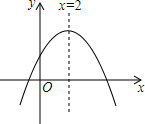 二次函数y=ax2+bx+c的图象如图所示,若点A(-1,y1),B(-2,y2)是其图象上的两点,则y1与y2的大小关系是( )
二次函数y=ax2+bx+c的图象如图所示,若点A(-1,y1),B(-2,y2)是其图象上的两点,则y1与y2的大小关系是( )| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 无法确定 |
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:选择题
| A. | (-1,2) | B. | (1,-2) | C. | (1,2) | D. | (2,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示的“杨辉三角”告诉了我们二项式乘方展开式的系数规律,如:第三行的三个数(1、2、1)恰好对应着(a+b)2的展开式a2+2ab+b2的系数;第四行的四个数恰好对应着(a+b)3=a3+3a2b+3ab2+b3的系数,根据数表中前五行的数字所反映的规律,回答:
如图所示的“杨辉三角”告诉了我们二项式乘方展开式的系数规律,如:第三行的三个数(1、2、1)恰好对应着(a+b)2的展开式a2+2ab+b2的系数;第四行的四个数恰好对应着(a+b)3=a3+3a2b+3ab2+b3的系数,根据数表中前五行的数字所反映的规律,回答:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,若△ABC中,∠C=90°,AD平分∠BAC,CD=3cm,AB=10cm,则△ABD的面积是( )
如图,若△ABC中,∠C=90°,AD平分∠BAC,CD=3cm,AB=10cm,则△ABD的面积是( )| A. | 15cm2 | B. | 10cm2 | C. | 5cm2 | D. | 2.5cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2x}{y}$与$\frac{4xy}{{2y}^{2}}$ | B. | $\frac{-2{mn}^{2}}{{4m}^{2}n}$与-$\frac{n}{2m}$ | ||
| C. | $\frac{-5y}{-2{5x}^{2}}$与$\frac{y}{{5x}^{2}}$ | D. | $\frac{{y}^{2}-{x}^{2}}{{(x-y)}^{2}}$与$\frac{x+y}{x-y}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com