
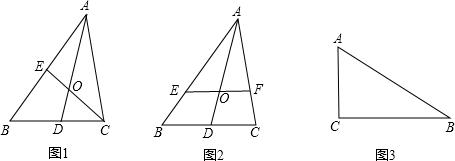
���� ��1������DE��������������λ�߶����õ�DE��AC��DE=$\frac{1}{2}$AC���������������ε��ж�������֤�����ɣ�
��2���ٸ��������ε����ĵĸ�������������ε�����ȵ������Ʊȵ�ƽ����ɣ�
�ڸ���ֱ��������б���ϵ�������б�ߵ�һ�롢�����ε����ĵ����ʽ�ɣ�
��� 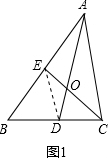 �⣺��1������DE��
�⣺��1������DE��
�����⣬D��EΪBC��AB�е㣬
��DEΪ��ABC����λ�ߣ�
��DE��AC��DE=$\frac{1}{2}$AC��
���ODE�ס�OAC�������Ʊ�Ϊ1��2��
��AO=2OD��
��$\frac{AO}{AD}=\frac{2}{3}$��
��2���١�EF��BC��
���AEO�ס�ABD�����Ʊ�Ϊ$\frac{2}{3}$��
��$\frac{AE}{AB}=\frac{2}{3}$��
ͬ������AEF�ס�ABC�����Ʊ�Ϊ$\frac{2}{3}$��
��$\frac{{{S_{��AEF}}}}{{{S_{��ABC}}}}=\frac{4}{9}$��
��$\frac{{{S_{��AEF}}}}{{{S_{�ı���EBCF}}}}=\frac{4}{5}$��
��С��˵����ȷ��
��Rt��ABC����ΪAB���е㣬��Ϊ��D��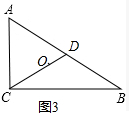
�ߡ�ACB=90�㣬AD=DB��
��CD=$\frac{1}{2}$AB=3cm��
����O������CD�ϣ��ɣ�1����$\frac{CO}{CD}=\frac{2}{3}$��
��OD=3��$\frac{1}{3}$=1cm��
���� ���⿼��������������ε��ж����������ʶ����Լ������ε����ĵ����ʣ��������ĵ�����ľ��������ĵ��Ա��е�ľ���֮��Ϊ2��1�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8a2b3 | B�� | 4ab3 | C�� | 8a2b4 | D�� | 4a2b3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 С����Сӱ��С��ѧ��������ѧ��У��ʽ�����˵��飬С������������������Ƴ���ͼ����ͳ��ͼ��A�������г���B�������У�C�����˳���
С����Сӱ��С��ѧ��������ѧ��У��ʽ�����˵��飬С������������������Ƴ���ͼ����ͳ��ͼ��A�������г���B�������У�C�����˳����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
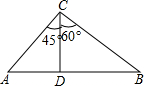 ��ͼ���ڡ�ABC�У�CD��AB����ACD=45�㣬��DCB=60�㣬AC=$40\sqrt{2}$����AB��
��ͼ���ڡ�ABC�У�CD��AB����ACD=45�㣬��DCB=60�㣬AC=$40\sqrt{2}$����AB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | $2\sqrt{2}$ | D�� | $2\sqrt{2}+1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com