Question

10．如图1，在平面直角坐标系中，已知抛物线y=ax²+bx+c的图象与x轴交于原点和点B（4，0），点A落在抛物线上，且OA=2，∠AOB=60°．
（1）则点A坐标为（1，$\sqrt{3}$），二次函数的解析式为y=-$\frac{\sqrt{3}}{3}$x²+$\frac{4\sqrt{3}}{3}$x．
（2）求证：△OAB为直角三角形．
（3）如图2：将△OAB绕着点A逆时针旋转90°得到△O₁AB₁，作出△O₁AB₁的外接圆⊙D，B₁O₁所在直线交x轴于点E．
①求点D的坐标；
②已知C（0，-3），连接BC，问：直线BC与圆D是否相切，并说明理由．

Answer 1

分析 （1）作AD⊥x轴，垂足为D．依据特殊锐角三角函数值可求得OD=1，AD=$\sqrt{3}$，从而可求得点A的坐标，将A、B点坐标代入函数解析式可求得a、b的值，从而得到二次函数的解析式；
（2）由两点间的距离公式可求得AB的长，然后依据勾股定理的逆定理进行证明即可；
（3）①延长B′O′交x轴与点E．由旋转的性质得到AB′=2$\sqrt{3}$，AO′=2，O′B′=4，从而得到OB′=2+2$\sqrt{3}$，在Rt△B′OE中由特殊锐角三角函数值可求得OE=1+$\sqrt{3}$，B′E=$\sqrt{3}+3$，由直角三角形的外心为斜边的中点可知B′D=2，从而可求得DE的长，故此可求得点D的坐标为（1$+\sqrt{3}$，1$+\sqrt{3}$）；②如图3所示：过点D作DF⊥CB，垂足为F，过点D作DE⊥x，交CB于点E．由勾股定理得BC=$\sqrt{O{C}^{2}+O{B}^{2}}$=5，依据待定系数法求得BC的解析式为y=$\frac{3}{4}x-3$，将x=$\sqrt{3}+1$，代入BC的解析式求得点E的纵坐标，从而可求得DE的长为$\frac{\sqrt{3}}{4}$+$\frac{13}{4}$，由OC∥DE，可知∠OCB=∠DEF，由锐角三角函数的定义可知：$\frac{DF}{DE}=\frac{OB}{BC}$，从而可求得DF=$\frac{\sqrt{3}+13}{5}$，由d＞r可知圆D与直线BC相离．

解答 解：（1）如图1所示：作AD⊥x轴，垂足为D．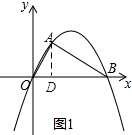

∵∠AOB=60°，
∴AD=OAsin∠AOD=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$，OD=AOcos∠AOD=2×$\frac{1}{2}$=1，．
∴点A的坐标为A（1，$\sqrt{3}$）．
将A、B点坐标代入函数解析式，得$\left\{\begin{array}{l}{a+b+c=\sqrt{3}}\\{16a+4b+c=0}\\{c=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{a=-\frac{\sqrt{3}}{3}}\\{b=\frac{4\sqrt{3}}{3}}\\{c=0}\end{array}\right.$，
抛物线的解析式为y=-$\frac{\sqrt{3}}{3}$x²+$\frac{4\sqrt{3}}{3}$x；
故答案为：（1，$\sqrt{3}$）；y=-$\frac{\sqrt{3}}{3}$x²+$\frac{4\sqrt{3}}{3}$x．
（2）证明：∵OA²=1²+（$\sqrt{3}$）²=4，AB²=（4-1）²+（$\sqrt{3}$）²=12，OB²=4²=16，
∴OA²+AB²=OB²．
∴△OAB是直角三角形．
（3）①如图2所示：延长B′O′交x轴与点E．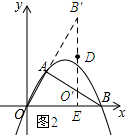

由旋转的性质得B₁在OA上，且AB′=AB=2$\sqrt{3}$，O′在AB上，且AO′=AO=2，O′B′=4．
∵OB′=OA+AB′，
∴OB′=2+2$\sqrt{3}$．
∵∠OAB=90°，∠AOB=60°，
∴∠ABO=30°．
由旋转的性质可知∠B′=∠ABO=30°．
∴∠B′+∠B′OE=30°+60°=90°．
∴OE=$\frac{1}{2}OB′$=1+$\sqrt{3}$，B′E=OB′×$\frac{\sqrt{3}}{2}$=$\sqrt{3}+3$．
∵点D是Rt△AB′O′的外心，
∴点D是B′O′的中点．
∴B′D=$\frac{1}{2}B′O′$=$\frac{1}{2}×4$=2．
∴ED=3+$\sqrt{3}-2$=$\sqrt{3}+1$．
∴点D的坐标为（1$+\sqrt{3}$，1$+\sqrt{3}$）．
②如图3所示：过点D作DF⊥CB，垂足为F，过点D作DE⊥x，交CB于点E．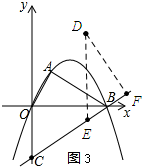

在Rt△OBC中，由勾股定理可知：BC=$\sqrt{O{C}^{2}+O{B}^{2}}$=5．
设BC的解析式为y=kx+b，将点C、B的坐标代入得：$\left\{\begin{array}{l}{4k+b=0}\\{b=-3}\end{array}\right.$，
解得：k=$\frac{3}{4}$，b=-3．
∴BC的解析式为y=$\frac{3}{4}x-3$．
将x=$\sqrt{3}+1$，代入BC的解析式得：y=$\frac{3}{4}$（$\sqrt{3}+1$）-3=$\frac{3\sqrt{3}}{4}$-$\frac{9}{4}$．
∴DE=$\sqrt{3}+1$-$\frac{3\sqrt{3}}{4}$+$\frac{9}{4}$=$\frac{\sqrt{3}}{4}$+$\frac{13}{4}$．
∵OC∥DE，
∴∠OCB=∠DEF．
∴$\frac{DF}{DE}=\frac{OB}{BC}$，即$\frac{DF}{\frac{\sqrt{3}+13}{4}}$=$\frac{4}{5}$．
∴DF=$\frac{\sqrt{3}+13}{5}$．
∵$\frac{\sqrt{3}+13}{5}＞2$，
∴d＞r．
∴圆D与直线BC相离．
∴直线BC与圆D不相切．

点评 本题主要考查的是二次函数的综合应用，解答本题主要应用了特殊锐角三角函数值、待定系数法求一次函数、二次函数的解析式、勾股定理的逆定理的应用、直线和圆的位置关系，掌握问题（3）中辅助线的作法，依据锐角三角函数的定义求得DF的长度是解题的关键．