Question

4．如图1，抛物线y=ax²+bx+c（a＞0）的顶点为M，直线y=m与x轴平行，且与抛物线交于点A，B，若△AMB为等腰直角三角形，我们把抛物线上A、B两点之间的部分与线段AB围成的图形称为该抛物线对应的准蝶形，线段AB称为碟宽，顶点M称为碟顶，点M到线段AB的距离称为碟高．

（1）抛物线y=$\frac{1}{2}$x²对应的碟宽为4；抛物线y=4x²对应的碟宽为$\frac{1}{2}$；抛物线y=ax²（a＞0）对应的碟宽为$\frac{2}{a}$；抛物线y=a（x-2）²+3（a＞0）对应的碟宽$\frac{2}{a}$；
（2）若抛物线y=ax²-4ax-$\frac{5}{3}$（a＞0）对应的碟宽为6，且在x轴上，求a的值；
（3）将抛物线y_n=a_nx²+b_nx+c_n（a_n＞0）的对应准蝶形记为F_n（n=1，2，3，…），定义F₁，F₂，…..F_n为相似准蝶形，相应的碟宽之比即为相似比．若F_n与F_n-1的相似比为$\frac{1}{2}$，且F_n的碟顶是F_n-1的碟宽的中点，现在将（2）中求得的抛物线记为y₁，其对应的准蝶形记为F₁．
①求抛物线y₂的表达式；
②若F₁的碟高为h₁，F₂的碟高为h₂，…F_n的碟高为h_n．则h_n=$\frac{3}{2n-1}$，F_n的碟宽右端点横坐标为2+$\frac{3}{2n-1}$；F₁，F₂，…．F_n的碟宽右端点是否在一条直线上？若是，直接写出该直线的表达式；若不是，请说明理由．

Answer 1

分析 （1）根据定义易算出含具体值的抛物线y=$\frac{1}{2}$x²，抛物线y=4x²的碟宽，且都利用端点（第一象限）横纵坐标相等．推广至含字母的抛物线y=ax²（a＞0），类似．而抛物线y=a（x-2）²+3（a＞0）为顶点式，可看成y=ax²平移得到，则发现碟宽只和a有关．
（2）根据（1）的结论，根据碟宽易得a的值．
（3）①由y₁，易推y₂．②结合画图，易知h₁，h₂，h₃，…，h_n-1，h_n都在直线x=2上，但证明需要有一般推广，可以考虑h_n∥h_n-1，且都过F_n-1的碟宽中点，进而可得．另画图时易知碟宽有规律递减，所以推理也可得右端点的特点．对于“F₁，F₂，…，F_n的碟宽右端点是否在一条直线上？”，如果写出所有端点规律似乎很难，找规律更难，所以可以考虑基础的几个图形关系，如果相邻3个点构成的两条线段不共线，则结论不成立，反则结论成立．求直线方程只需考虑特殊点即可．

解答 解：（1）4；$\frac{1}{2}$；$\frac{2}{a}$；$\frac{2}{a}$．
分析如下：
∵a＞0，
∴y=ax²的图象大致如下：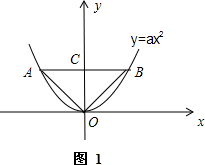

其必过原点O，记AB为其碟宽，AB与y轴的交点为C，连接OA，OB．
∵△OAB为等腰直角三角形，AB∥x轴，
∴OC⊥AB，
∴∠AOC=∠BOC=$\frac{1}{2}$∠AOB=$\frac{1}{2}$•90°=45°，
∴△ACO与△BCO亦为等腰直角三角形，
∴AC=OC=BC，
∴x_A=y_A，x_B=y_B，代入y=ax²，
∴A（-$\frac{1}{a}$，$\frac{1}{a}$），B（$\frac{1}{a}$，$\frac{1}{a}$），C（0，$\frac{1}{a}$），
∴AB=$\frac{2}{a}$，OC=$\frac{1}{a}$，
即y=ax²的碟宽为$\frac{2}{a}$．
①抛物线y=$\frac{1}{2}$x²对应的a=$\frac{1}{2}$，得碟宽$\frac{2}{a}$为4；
②抛物线y=4x²对应的a=4，得碟宽为$\frac{2}{a}$为$\frac{1}{2}$；
③抛物线y=ax²（a＞0），碟宽为$\frac{2}{a}$；
④抛物线y=a（x-2）²+3（a＞0）可看成y=ax²向右平移2个单位长度，再向上平移3个单位长度后得到的图形，
∵平移不改变形状、大小、方向，
∴抛物线y=a（x-2）²+3（a＞0）的准碟形≌抛物线y=ax²的准碟，
∵抛物线y=ax²（a＞0），碟宽为$\frac{2}{a}$，
∴抛物线y=a（x-2）²+3（a＞0），碟宽为$\frac{2}{a}$．

（2）∵y=ax²-4ax-$\frac{5}{3}$=a（x-2）²-（4a+$\frac{5}{3}$），
∴同（1），其碟宽为$\frac{2}{a}$，
∵y=ax²-4ax-$\frac{5}{3}$的碟宽为6，
∴$\frac{2}{a}$=6，
解得 a=$\frac{1}{3}$，
∴y=$\frac{1}{3}$（x-2）²-3．

（3）①∵F₁的碟宽：F₂的碟宽=2：1，
∴$\frac{2}{{a}_{1}}$=$\frac{4}{{a}_{2}}$，
∵a₁=$\frac{1}{3}$，
∴a₂=$\frac{2}{3}$．
∵y=$\frac{1}{3}$（x-2）²-3的碟宽AB在x轴上（A在B左边），
∴A（-1，0），B（5，0），
∴F₂的碟顶坐标为（2，0），
∴y₂=$\frac{2}{3}$（x-2）²．
②∵F_n的准碟形为等腰直角三角形，
∴F_n的碟宽为2h_n，
∵2h_n：2h_n-1=1：2，
∴h_n=$\frac{1}{2}$h_n-1=（$\frac{1}{2}$）²h_n-2=（$\frac{1}{2}$）³h_n-3=…=（$\frac{1}{2}$）^n-1h₁，
∵h₁=3，
∴h_n=$\frac{3}{2n-1}$．
∵h_n∥h_n-1，且都过F_n-1的碟宽中点，
∴h₁，h₂，h₃，…，h_n-1，h_n都在一条直线上，
∵h₁在直线x=2上，
∴h₁，h₂，h₃，…，h_n-1，h_n都在直线x=2上，
∴F_n的碟宽右端点横坐标为2+$\frac{3}{2n-1}$．
另，F₁，F₂，…，F_n的碟宽右端点在一条直线上，直线为y=-x+5．
分析如下：
考虑F_n-2，F_n-1，F_n情形，关系如图2，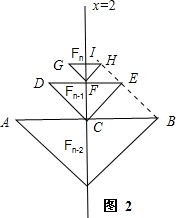

F_n-2，F_n-1，F_n的碟宽分别为AB，DE，GH；C，F，I分别为其碟宽的中点，都在直线x=2上，连接右端点，BE，EH．
∵AB∥x轴，DE∥x轴，GH∥x轴，
∴AB∥DE∥GH，
∴GH平行相等于FE，DE平行相等于CB，
∴四边形GFEH，四边形DCBE都为平行四边形，
∴HE∥GF，EB∥DC，
∵∠GFI=$\frac{1}{2}$•∠GFH=$\frac{1}{2}$•∠DCE=∠DCF，
∴GF∥DC，
∴HE∥EB，
∵HE，EB都过E点，
∴HE，EB在一条直线上，
∴F_n-2，F_n-1，F_n的碟宽的右端点是在一条直线，
∴F₁，F₂，…，F_n的碟宽的右端点是在一条直线．
∵F₁：y₁=$\frac{1}{3}$（x-2）²-3准碟形右端点坐标为（5，0），
  F₂：y₂=$\frac{2}{3}$（x-2）²准碟形右端点坐标为（2+$\frac{3}{2}$，$\frac{3}{2}$），
∴待定系数可得过两点的直线为y=-x+5，
∴F₁，F₂，…，F_n的碟宽的右端点是在直线y=-x+5上．
故答案是：（1）4、$\frac{1}{2}$、$\frac{2}{a}$、$\frac{2}{a}$；（2）$\frac{1}{3}$；（3）①y₂=$\frac{2}{3}$（x-2）²；②$\frac{3}{2n-1}$，2+$\frac{3}{2n-1}$，y=-x+5．

点评 本题考查了二次函数综合题，学生对新知识的学习、理解与应用能力．题目中主要涉及特殊直角三角形，二次函数解析式与图象性质，多点共线证明等知识，综合难度较高，学生清晰理解有一定困难．