
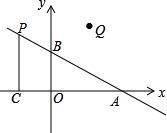
 如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(4,0),点B的坐标为(0,b)(b>0),点P是直线AB上位于第二象限内的一个动点,过点P作PC⊥x轴于点C,记点P关于y轴的对称点为Q,设点P的横坐标为a.
如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(4,0),点B的坐标为(0,b)(b>0),点P是直线AB上位于第二象限内的一个动点,过点P作PC⊥x轴于点C,记点P关于y轴的对称点为Q,设点P的横坐标为a.分析 (1)①由题意确定出B坐标,设直线AB解析式为y=kx+b,把A与B坐标代入求出k与b的值,即可求出AB解析式;②由AQ=QO以及OA的长,确定出Q横坐标,根据P与Q关于y轴对称,得出P横坐标,代入直线AB解析式求出纵坐标,即可确定出P坐标;
(2)同时存在a、b,使得△QAC是等腰直角三角形,分两种情况考虑:①若∠QAC=90°;②若∠AQC=90°,分别求出a与b的值即可.
解答 解:(1)①由A(4,0),B(0,3),
设直线AB解析式为y=kx+b,
把A与B坐标代入得:$\left\{\begin{array}{l}{4k+b=0}\\{b=3}\end{array}\right.$,
解得:k=-$\frac{3}{4}$,b=3,
则直线AB解析式为y=-$\frac{3}{4}$x+3;
②∵QA=QO,OA=4,
∴xQ=2,
∵点P关于y轴的对称点为Q,
∴xP=-2,
代入直线AP解析式得-$\frac{3}{4}$×(-2)+3=$\frac{9}{2}$,
则P坐标得P(-2,$\frac{9}{2}$);
(2)①若∠QAC=90°,如图1所示,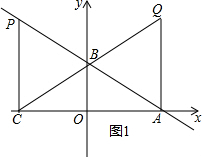
∴xQ=4,
∴a=xP=-4,
∴AC=AQ=8,即P(-4,8),
∴直线AP解析式为y=-x+4,
∴a=-4,b=4;
②若∠AQC=90°,如图2所示,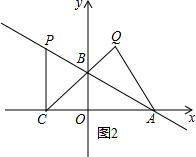
则AC=4-a=2CH=-4a,
∴a=-$\frac{4}{3}$,
∴xP=-$\frac{4}{3}$,yP=yq=$\frac{8}{3}$,即P(-$\frac{4}{3}$,$\frac{8}{3}$),
∴直线AP解析式为y=-$\frac{1}{2}$x+2,
∴a=-$\frac{4}{3}$,b=2,
③P、Q重合于(0,4)时,△QCA也是等腰直角三角形,此时a=0,b=4
综上所示,a=-4,b=4或a=-$\frac{4}{3}$,b=2或a=0,b=4.
点评 此题属于一次函数综合题,涉及的知识有:待定系数法确定一次函数解析式,等腰直角三角形的性质,坐标与图形性质,熟练掌握一次函数的性质是解本题的关键.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:解答题
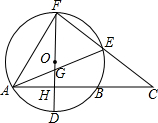 如图,⊙O的直径FD⊥弦AB于点H,E是$\widehat{BF}$上一动点,连结FE并延长交AB的延长线于点C,AB=8,HD=2.
如图,⊙O的直径FD⊥弦AB于点H,E是$\widehat{BF}$上一动点,连结FE并延长交AB的延长线于点C,AB=8,HD=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 成本 | 标价 | 售价 |
| x | x+60 | 0.8x+48 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
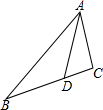 如图,在△ABC中,点D在边BC上,若∠BAD=∠CAD,AB=6,AC=3,S△ABD=3,则S△ACD=$\frac{3}{2}$.
如图,在△ABC中,点D在边BC上,若∠BAD=∠CAD,AB=6,AC=3,S△ABD=3,则S△ACD=$\frac{3}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com