Question

10．已知某二次函数的对称轴平行于y轴，图象顶点为A（1，0），且与y轴交于点B（0，1）
（1）求该二次函数的解析式；
（2）设C为该二次函数图象上横坐标为2的点，记$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，试用$\overrightarrow{a}$、$\overrightarrow{b}$表示$\overrightarrow{OC}$．

Answer 1

分析 （1）由图象顶点为A（1，0），首先可设该二次函数的解析式为：y=a（x-1）²，又由与y轴交于点B（0，1），可利用待定系数法求得答案；
（2）首先求得点C的坐标，然后根据题意作出图形，易求得$\overrightarrow{BC}$，然后由三角形法则，求得答案．

解答 解：（1）设该二次函数的解析式为：y=a（x-1）²，
∵与y轴交于点B（0，1），
∴a=1，
∴该二次函数的解析式为：y=（x-1）²；

（2）∵C为该二次函数图象上横坐标为2的点，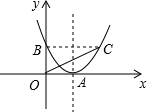
∴y=（2-1）²=1，
∴C点坐标为：（2，1），
∴BC∥x轴，
∴$\overrightarrow{BC}$=2$\overrightarrow{OA}$=2$\overrightarrow{a}$，
∴$\overrightarrow{OC}$=$\overrightarrow{OB}$+$\overrightarrow{BC}$=$\overrightarrow{b}$+2$\overrightarrow{a}$．

点评 此题考查了平面向量的知识、待定系数法求函数的解析式以及点与二次函数的关系．注意结合题意画出图形，利用图形求解是关键．