【题目】椭圆
上一点A关于原点的对称点为B，F为椭圆的右焦点，AF⊥BF，∠ABF＝
，
，
，则椭圆的离心率的取值范围为_______．
【答案】
【解析】
设左焦点为F′，根据椭圆定义：|AF|+|AF′|=2a，根据B和A关于原点对称可知|BF|=|AF′|，推知|AF|+|BF|=2a，又根据O是Rt△ABF的斜边中点可知|AB|=2c，在Rt△ABF中用a和c分别表示出|AF|和|BF|代入|AF|+|BF|=2a中即可表示出
即离心率e，进而根据α的范围确定e的范围．
∵B和A关于原点对称，∴B也在椭圆上，设左焦点为F′
根据椭圆定义：|AF|+|AF′|=2a
又∵|BF|=|AF′|∴|AF|+|BF|=2a …①
O是Rt△ABF的斜边中点，∴|AB|=2c
又|AF|=2csinα …②
|BF|=2ccosα …③
②③代入①2csinα+2ccosα=2a
∴=
即e==
∵a∈[
，
]，∴
≤α+≤
∴
≤sin（α+）≤1 ∴
≤e≤
故答案为：[，]
阅读快车系列答案科目：高中数学 来源： 题型：
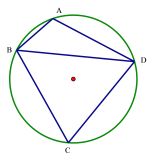
【题目】某城市在进行规划时，准备设计一个圆形的开放式公园.为达到社会和经济效益双丰收.园林公司进行如下设计，安排圆内接四边形
作为绿化区域，其余作为市民活动区域.其中
区域种植花木后出售，
区域种植草皮后出售，已知草皮每平方米售价为
元，花木每平方米的售价是草皮每平方米售价的三倍. 若
km ，
km
（1）若
km ，求绿化区域的面积；
（2）设
，当
取何值时，园林公司的总销售金额最大.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆
过点
,且圆心在直线
上．
（1）求圆的方程；
（2）平面上有两点
，点
是圆上的动点，求
的最小值；
（3）若
是
轴上的动点，
分别切圆于
两点，试问：直线
是否恒过定点？若是，求出定点坐标，若不是，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，
是由两个全等的菱形
和
组成的空间图形，
，∠BAF＝∠ECD＝60°.
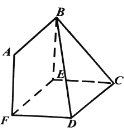
（1）求证：
；
（2）如果二面角B－EF－D的平面角为60°，求直线
与平面
所成角的正弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于无穷数列{an}，记T={x|x=aj﹣ai，i＜j}，若数列{an}满足：“存在t∈T，使得只要am﹣ak=t（m，k∈N*，m＞k），必有am+1﹣ak+1=t”，则称数列具有性质P（t）．
（1）若数列{an}满足
，判断数列{an}是否具有性质P（2）？是否具有性质P（4）？说明理由；
（2）求证：“T是有限集”是“数列{an}具有性质P（0）”的必要不充分条件；
（3）已知{bn}是各项均为正整数的数列，且{bn}既具有性质P（2），又具有性质P（5），求证：存在正整数N，使得aN，aN+1，aN+2，…，aN+K，…是等差数列．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】点
为
所在的平面内，给出下列关系式：
①
；
②
；
③
.
则点依次为的（ ）
A.内心、重心、垂心B.重心、内心、垂心C.重心、内心、外心D.外心、垂心、重心
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的左、右焦点分别为
，
，过点
的直线与椭圆
交于
两点，延长
交椭圆于点
，
的周长为8.
（1）求的离心率及方程；
（2）试问：是否存在定点
，使得
为定值？若存在，求
；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线
，和两点
，给出如下结论其中真命题的序号是________
①当
变化时，
与
分别经过定点
和
；
②不论为何值时，与都互相垂直；
③如果与交于点
，则
的最大值是2；
④
为直线
上的点，则
的最小值是
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
