
【题目】已知函数![]() (
(![]() ).
).
(1)若![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(2)若![]() ,证明:
,证明:![]() 在
在![]() 有唯一的极值点x,且
有唯一的极值点x,且![]() .
.
【答案】(1)![]() .(2)见解析
.(2)见解析
【解析】
(1)计算![]() 得到
得到![]() ,再证明当
,再证明当![]() (
(![]() )时,
)时,![]() ,先证明
,先证明![]() (
(![]() ),讨论
),讨论![]() 和
和![]() 两种情况,计算得到证明.
两种情况,计算得到证明.
(2)求导得到![]() ,
,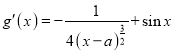 ,得到存在唯一实数
,得到存在唯一实数![]() ,使
,使![]() ,存在唯一实数
,存在唯一实数![]() ,使
,使![]() ,得到
,得到![]() ,得到证明.
,得到证明.
(1)由![]() ,得
,得![]() ,即
,即![]() ,解得
,解得![]() ,
,![]() ,
,
以下证明,当![]() (
(![]() )时,
)时,![]() .
.
为此先证:![]() (
(![]() ).
).
若![]() ,则
,则![]() ;
;
若![]() ,则
,则![]() .
.
令![]() (
(![]() ),可知
),可知![]() ,函数单调递增,
,函数单调递增,
故![]() ,即
,即![]() (
(![]() ),
),
综上所述:![]() (
(![]() ).
).
若![]() (
(![]() ),则当
),则当![]() 时,
时,![]() ,
,
故![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,由
,由![]() (
(![]() ),
),
得![]() .
.
故当![]() (
(![]() )时,
)时,![]() .
.
综上,所求a的取值范围是![]() .
.
(2)![]() ,令
,令![]() ,
,
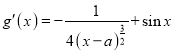 ,∵
,∵![]() ,∴
,∴![]() 是
是![]() 上的增函数,
上的增函数,
又![]() ,
,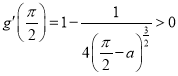 ,
,
故存在唯一实数![]() ,使
,使![]() ,当
,当![]() 时,
时,![]() ,
,![]() 递减;当
递减;当![]() 时,
时,![]() ,
,![]() 递增.
递增.
又![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,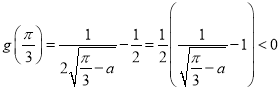 ,
,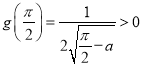 .
.
故存在唯一实数![]() ,使
,使![]() .
.
当![]() 时,
时,![]() ,
,![]() 递减;
递减;
当![]() 时,
时,![]() ,
,![]() 递增.
递增.
所以![]() 在区间
在区间![]() 有唯一极小值点
有唯一极小值点![]() ,且极小值为
,且极小值为![]() .
.
又由![]() ,得
,得![]() ,
,
∴![]() .
.
又![]() .
.
以下只需证明,即证![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .
.
则![]() ,所以
,所以![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,![]() ,E、F分别为AD,BC的中点.以EF为折痕把四边形EFCD折起,使点C到达点M的位置,点D到达点N的位置,且
,E、F分别为AD,BC的中点.以EF为折痕把四边形EFCD折起,使点C到达点M的位置,点D到达点N的位置,且![]() .
.

(1)求证:![]() 平面NEB;
平面NEB;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小值为0,其中
的最小值为0,其中![]() .
.
(1)求![]() 的值;
的值;
(2)若对任意的![]() ,有
,有![]() 恒成立,求实数
恒成立,求实数![]() 的最小值;
的最小值;
(3)记![]() ,
,![]() 为不超过
为不超过![]() 的最大整数,求
的最大整数,求![]() 的值.
的值.
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年,全国各地区坚持稳中求进工作总基调,经济运行总体平稳,发展水平迈上新台阶,发展质量稳步上升,人民生活福祉持续增进,全年最终消费支出对国内生产总值增长的贡献率为57.8%.下图为2019年居民消费价格月度涨跌幅度:(同比![]() (本期数-去年同期数)/去年同期数
(本期数-去年同期数)/去年同期数![]() ,环比
,环比![]() (本期数-上期数)/上期数
(本期数-上期数)/上期数![]()
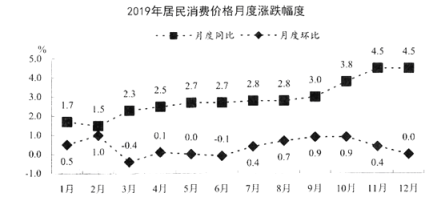
下列结论中不正确的是( )
A.2019年第三季度的居民消费价格一直都在增长
B.2018年7月份的居民消费价格比同年8月份要低一些
C.2019年全年居民消费价格比2018年涨了2.5%以上
D.2019年3月份的居民消费价格全年最低
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() .
.
(1)求证:数列![]() 等差数列;
等差数列;
(2)当![]() 时,记
时,记![]() ,是否存在正整数
,是否存在正整数![]() 、
、![]() ,使得
,使得![]() 、
、![]() 、
、![]() 成等比数列?若存在,求出所有满足条件的数对
成等比数列?若存在,求出所有满足条件的数对![]() ;若不存在,请说明理由;
;若不存在,请说明理由;
(3)若数列![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 是公比为
是公比为![]() 的等比数列,求最小正整数
的等比数列,求最小正整数![]() ,使得当
,使得当![]() 时,
时,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若函数![]() 有两个不同的极值点
有两个不同的极值点![]() 、
、![]() ,求证:
,求证:![]() ;
;
(3)设![]() ,函数
,函数![]() 的反函数为
的反函数为![]() ,令
,令![]() ,
,![]() 、
、![]() 、
、![]() ,
,![]() ,
,![]() 且
且![]() ,若
,若![]() 时,对任意的
时,对任意的![]() 且
且![]() ,
,![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() .
.

(1)过![]() 作截面与线段
作截面与线段![]() 交于点H,使得
交于点H,使得![]() 平面
平面![]() ,试确定点H的位置,并给出证明;
,试确定点H的位置,并给出证明;
(2)在(1)的条件下,若二面角![]() 的大小为
的大小为![]() ,试求直线
,试求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com