
![]()
![]()

 2007届高三数学期中测试卷
2007届高三数学期中测试卷
一、选择题(本题每小题5分,共50分)
1.已知角 的终边经过点
的终边经过点 ,且
,且 ,则
,则 的值是( )
的值是( )
A、 B、
B、 C、
C、 D、
D、
2.点P在直线 上,PA、PB与圆
上,PA、PB与圆 相切于A、B两点,则四边形PAOB面积的最小值为( )
相切于A、B两点,则四边形PAOB面积的最小值为( )
A.24
B.
3.  ,
, 分别是直角坐标系内
分别是直角坐标系内 轴、
轴、 轴正方向上的单位向量,在同一直线上有A、B、C三个点,
轴正方向上的单位向量,在同一直线上有A、B、C三个点, ,若
,若 ,则
,则 ,
, 的值分别为( )
的值分别为( )
A.  或
或 B.
B.  或
或
C .  或
或 D.
D.  或
或
4. 函数f(x)是R上的奇函数,当x<0时,f(x)=()x,则 的值为 ( )
的值为 ( )
A.2
B.-
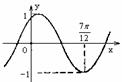 5.将函数
5.将函数 的图象按向量
的图象按向量 平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )
平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )
A.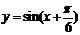 B.
B.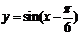
C.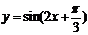 D.
D.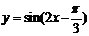
6.在等比数列{an}中,S4=1,S8=3,则a17+a18+a19+a20的值是( )
A.14
B.
7.已知向量a=(cos75°,sin75°),b=(cos15°,sin15°),那么|a-b|的值是( )
A.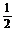 B.
B.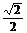 C.
C.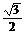 D.1
D.1
8.等比数列{an}公比为a(a≠1),首项为b,Sn是前n项和,对任意的n∈N+ ,点(Sn ,Sn+1)在 ( )
A.直线y=ax-b上 B.直线y=bx+a上
C.直线y=bx-a上 D.直线y=ax+b上
9. 在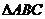 中,
中,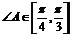 ,其面积为S,则
,其面积为S,则 的取值范围是( )
的取值范围是( )
A.  B.
B. 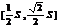 C.
C. 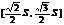 D.
D. 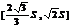
10.已知a1,a2,a3,…,a8为各项都大于零的数列,则“a1+a8<a4+a
A.充分且必要条件 B.充分但非必要条件
C.必要但非充分条件 D.既不充分也不必要条件
 二、填空题(本题每小题5分,共30分)
二、填空题(本题每小题5分,共30分)
11、可行域如图(含边界),使目标函数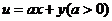 取得最大值的最优解有无数多个,则
取得最大值的最优解有无数多个,则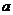 的值为
的值为
12.已知 为互相垂直的单位向量,
为互相垂直的单位向量,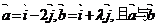 的夹角为锐角,则实数
的夹角为锐角,则实数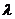 的取值范围是
的取值范围是
13.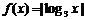 ,不等式
,不等式 >
>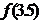 的解集为
的解集为
14. 对于函数 ,给出下列命题:①f(x)有最小值;②当a=0时,f
(x)的值域为R;③当a>0时,f (x)在区间
,给出下列命题:①f(x)有最小值;②当a=0时,f
(x)的值域为R;③当a>0时,f (x)在区间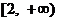 上有反函数;④若f (x)在区间
上有反函数;④若f (x)在区间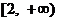 上是增函数,则实数a的取值范围是
上是增函数,则实数a的取值范围是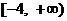 . 上述命题中正确的是
(填上所有正确命题序号) .
. 上述命题中正确的是
(填上所有正确命题序号) .
15.设P是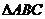 所在平面上的一点,
所在平面上的一点, ,
,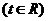 使P落在
使P落在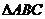 内部的
内部的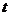 的取值范围是
_________。
的取值范围是
_________。
16.在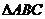 中,O为中线AD上的一个动点,若AD=4,则
中,O为中线AD上的一个动点,若AD=4,则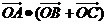 的最小值是_________
的最小值是_________
三、解答题(本大题共5小题,共70分):
17、已知A(3,0),B(0,3),C(cos ,sin
,sin ).
).
(1)若 =-1,求sin2
=-1,求sin2 的值;
的值;
(2)若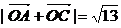 ,且
,且 ∈(0,π),求
∈(0,π),求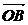 与
与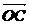 的夹角.
的夹角.
18、正数数列{an}的前n项和为Sn,且2.
(1) 试求数列{an}的通项公式;
(2)设bn=,{bn}的前n项和为Tn,求证:Tn<.
19、函数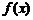 的定义域为R,并满足以下条件:
的定义域为R,并满足以下条件:
①对任意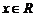 ,有
,有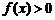 ;②对任意
;②对任意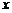 、
、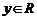 ,有
,有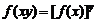 ;③
;③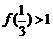
(1)求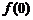 的值,并证明
的值,并证明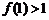 ;
;
(2)求证: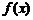 在R上是单调增函数;
在R上是单调增函数;
(3)若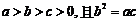 ,求证:
,求证: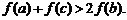
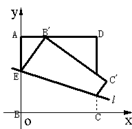
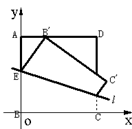
20、如图边长为2的正方形纸片ABCD,以动直线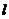 为折痕将正方形向上翻折,使得每次翻折后点B都落在边AD上,记为
为折痕将正方形向上翻折,使得每次翻折后点B都落在边AD上,记为 ;折痕
;折痕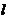 与AB交于点E,点M满足关系式
与AB交于点E,点M满足关系式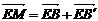 。
。
(1)求点M的轨迹方程;(2)曲线C是由点M轨迹及其关于边AB对称的曲线组成,F(0, 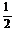 ),过点F的直线交曲线C于P、Q两点,且
),过点F的直线交曲线C于P、Q两点,且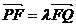 ,求
,求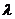 的范围。
的范围。
21、设函数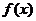 的定义域、值域均为
的定义域、值域均为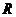 ,
,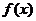 的反函数为
的反函数为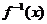 ,且对于任意实数
,且对于任意实数 ,均有
,均有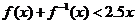 ,定义数列
,定义数列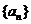 :
: .
.
(1)求证: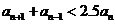 ;(2)设
;(2)设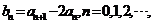 求证:
求证: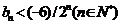 ;
;
(3)是否存在常数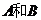 ,同时满足:①当
,同时满足:①当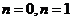 时,有
时,有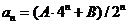 ;② 当
;② 当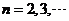 .时,有
.时,有 成立.如果存在满足上述条件的实数
成立.如果存在满足上述条件的实数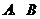 ,求出
,求出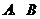 的值;如果不存在,证明你的结论。
的值;如果不存在,证明你的结论。
2007届高三数学第一学期期中测试卷答案
三、解答题(本大题共5小题,共70分):
17(1)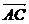 =(cos
=(cos -3,sin
-3,sin ),
),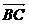 =(cos
=(cos ,sin
,sin -3),
-3),
∴由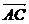 ?
?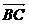 =-1,得(cos
=-1,得(cos -3)cos
-3)cos +sin
+sin (sin
(sin -3)=-1,
-3)=-1,
∴cos +sin
+sin =
=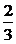 , 两边平方,得1+sin2
, 两边平方,得1+sin2 =
=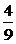 ,∴sin2
,∴sin2 =-
=-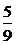 .
.
(2)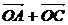 =(3+cos
=(3+cos ,sin
,sin ),∴(3+cos
),∴(3+cos )2+sin2
)2+sin2 =13, ∴cos
=13, ∴cos =
=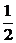 ,
,
∵ ∈(0,π),∴
∈(0,π),∴ =
=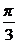 ,sin
,sin =
=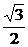 , ∴
, ∴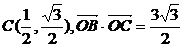 ,
,
设 与
与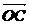 的夹角为θ,则
的夹角为θ,则
cosθ=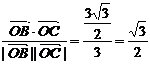 , ∴θ=
, ∴θ=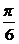 即为所求.
即为所求.
18.(1)∵an>0,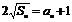 ,∴
,∴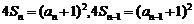 ,则当n≥2时,
,则当n≥2时,
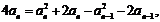 即
即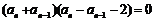 ,而an>0,∴
,而an>0,∴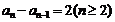
又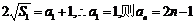
(2)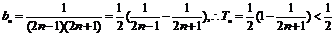
19. (1)∵对任意x、y∈R,有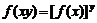
 ∴当
∴当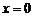 时
时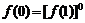
∵任意x∈R,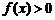
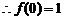

(2)
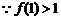
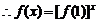 是R上单调增函数 即
是R上单调增函数 即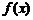 是R上单调增函数;
是R上单调增函数;
(3)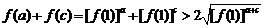
而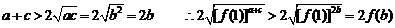
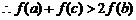
20. 解答:(1)设E(0,t),B’(x0,2),M(x,y),则在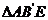 中可求得
中可求得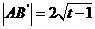 ,∴
,∴
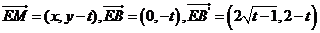
又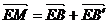 ,代入可得:
,代入可得: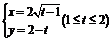
消去t得: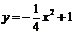 (0≤x≤2)(8分)
(0≤x≤2)(8分)
(2)F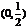 ,设P
,设P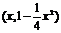 ,
,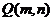
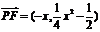 ;
;
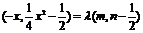
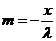 ,
, 
将Q(m,n)代入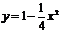 得
得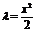
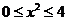
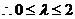
又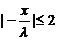
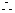
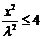 即
即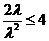 解得
解得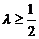
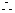
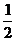 ≤
≤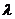 ≤2(14分)
≤2(14分)
21. 解:(1)由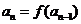 ,得
,得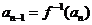 ,
,
又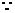
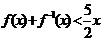 ,令
,令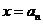 得
得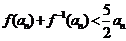 ,即
,即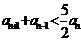 ;
;
(2)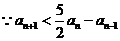 ,
,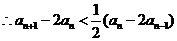 ,即
,即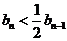 ,又
,又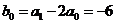 ,
,
所以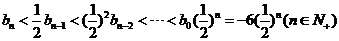
所以
(3)假设存在常数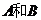 ,使得当
,使得当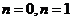 时,有
时,有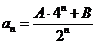 ,则
,则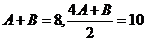 ,解得
,解得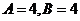 。
。
由 ,即
,即 ,两边同时除以
,两边同时除以 ,得
,得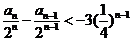 ,分别令
,分别令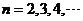 得
得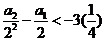 ,
,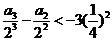 ,
,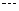
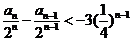 ,将这
,将这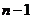 个不等式想加得:
个不等式想加得: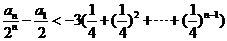
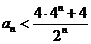 。
。
即存在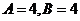 ①当
①当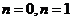 时,有
时,有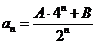 ;② 当
;② 当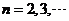 .时,有
.时,有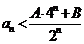 成立.
成立.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com