
高三数学专题讲座(复数)2001年5月10日
1、(2000年)在复平面内,把复数 对应的向量按顺时针方向旋转
对应的向量按顺时针方向旋转 ,所得向量对应的复数是
,所得向量对应的复数是
(A) (B)
(B) (C)
(C) (D)
(D)
2、(2000年春季)复数 则
则 在复平面内的对应点位于
在复平面内的对应点位于
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
3、(2000年春季)设复数z1=2sin +icos
+icos
 在复平面上对应向量
在复平面上对应向量 ,将
,将 按顺时针方向旋转
按顺时针方向旋转 后得到向量
后得到向量 ,
, 对应的复数为Z2=r(cosj+isinj),则tgj=
对应的复数为Z2=r(cosj+isinj),则tgj=
(A) (B)
(B) (C)
(C) (D)
(D)
4、(2000年上海)设复数 满足
满足 ,且
,且 在复平面上对应的点在第二、四象限的角平分线上,
在复平面上对应的点在第二、四象限的角平分线上, ,求
,求 和
和 的值.
的值.
5、(1999年)设复数 ,求函数
,求函数 的最大值及对应的
的最大值及对应的 的值。
的值。
6、(1998年)复数?i的一个立方根是i,它的另外两个立方根是
(A)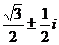 (B)
(B)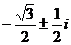 (C)
(C)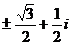 (D)
(D)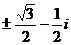
7、(1997年)已知复数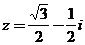 ,
,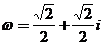 ,复数
,复数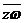 、
、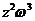 在复平面上所对应的点分别为P、Q。证明△OPQ是等腰直角三角形(其中O为原点)
在复平面上所对应的点分别为P、Q。证明△OPQ是等腰直角三角形(其中O为原点)
8、(1996年)复数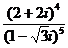 等于
等于
(A)、1+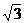 i (B)、-1+
i (B)、-1+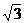 i (C)、1-
i (C)、1-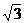 i (D)-1-
i (D)-1-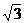 i
i
9、(1995年)在复平面上,一个正方形的四个顶点按照逆时针方向依次为Z1, Z2 ,Z3
,O(其中O是原点),已知Z2对应复数Z2=1+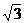 i。求Z1和Z2对应的复数。
i。求Z1和Z2对应的复数。
10、(1994年)如果复数z满足 |z+ i |+ | z-i |=2,那么 | z+i+1 |的最小值是
(A)1 (B)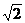 (C)2 (D)
(C)2 (D)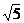
11、(1994年)已知z=1+i,(1)设w=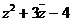 ,求w的三角形式;
,求w的三角形式;
(2)如果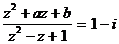 ,求实数a、b的值。
,求实数a、b的值。
12、(1993年)设复数z=cosq+isinq (0<q<p),w=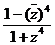 ,并且|w|=
,并且|w|=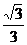 ,argw<
,argw<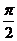 , 求 q
, 求 q
13、(2001年春季)已知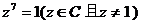 .
.
(Ⅰ)证明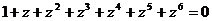 ;
;
(Ⅱ)设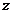 的辐角为
的辐角为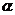 ,求
,求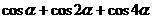 的值.
的值.
14、(2000年上海)复数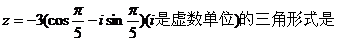
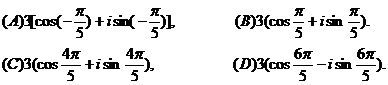
15、(2000年上海)已知复数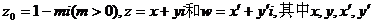 均为实数,
均为实数,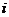 为虚数单位,且对于任意复数
为虚数单位,且对于任意复数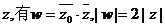 。
。
(1)试求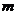 的值,并分别写出
的值,并分别写出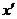 和
和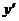 用
用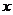 、
、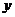 表示的关系式;
表示的关系式;
(2)将(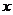 、
、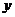 )作为点
)作为点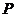 的坐标,(
的坐标,(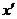 、
、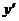 )作为点
)作为点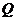 的坐标,上述关系可以看作是坐标平面上点的一个变换:它将平面上的点
的坐标,上述关系可以看作是坐标平面上点的一个变换:它将平面上的点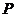 变到这一平面上的点
变到这一平面上的点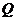 ,
,
当点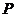 在直线
在直线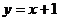 上移动时,试求点
上移动时,试求点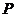 经该变换后得到的点
经该变换后得到的点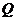 的轨迹方程;
的轨迹方程;
(3)是否存在这样的直线:它上面的任一点经上述变换后得到的点仍在该直线上?若存在,试求出所有这些直线;若不存在,则说明理由。
1、B
2、D
3、A
4、[解法一]设
而
又∵ 在复平面上对应的点在第二、四象限的角平分线上,
在复平面上对应的点在第二、四象限的角平分线上,
∴ ,得
,得 .
.
∴ . 即
. 即 ;
; ,
,
当 时,有
时,有 ,即
,即 ,得
,得 .
.
当 时,同理可得
时,同理可得 .
.
[解法二] ,∴
,∴ ,
,
得
或
 得
得 .
.
当 时,有
时,有 ,即
,即 ,得
,得 .
.
当 时,同理可得
时,同理可得 .
.
5、解:由
由 得
得
故

当且仅当 时,即
时,即 时,上式取等号.
时,上式取等号.
所以当 时,函数
时,函数 取最大值
取最大值
6、D
7、解:因为
因为
于是
由此得OP⊥OQ,|OP|=|OQ| .
由此知△OPQ有两边相等且其夹角为直角,故△OPQ为等腰直角三角形。
8、B
9、解:设Z1,Z3对应的复数分别为
依题设得


10、A
11、(1)
(2)
12、 ,
, 或
或
13、解:(Ⅰ)由 

 ,
,
得 . ……4分
. ……4分
因为  ,
, ,
,
所以  . ……6分
. ……6分
(Ⅱ)因为 ,
,
所以  ,而
,而 ,所以
,所以 ,
,
 ,同理
,同理 ,
, .
.
由(Ⅰ)知  ,
,
即  ,
,
所以  的实部为
的实部为 , ……8分
, ……8分
而 的辐角为
的辐角为 时,复数
时,复数 的实部为
的实部为
 ,
,
所以  ……12分
……12分
14、C
15、[解](1)由题设, ,
,
于是由 ,
…(3分)
,
…(3分)
因此由 ,
,
得关系式 …(5分)
…(5分)
[解](2)设点 在直线
在直线 上,则其经变换后的点
上,则其经变换后的点 满足
满足
 ,
…(7分)
,
…(7分)
消去 ,得
,得 ,
,
故点 的轨迹方程为
的轨迹方程为 …(10分)
…(10分)
[解](3)假设存在这样的直线,∵平行坐标轴的直线显然不满足条件,
∴所求直线可设为 ,
…(12分)
,
…(12分)
[解法一]∵该直线上的任一点 ,其经变换后得到的点
,其经变换后得到的点
 仍在该直线上,
仍在该直线上,
∴ ,
,
即 ,
,
当 时,方程组
时,方程组 无解,
无解,
故这样的直线不存在。 …(16分)
当 时,由
时,由
得 ,
,
解得 或
或 ,
,
故这样的直线存在,其方程为 或
或 ,
…(18分)
,
…(18分)
[解法二]取直线上一点 ,其经变换后的点
,其经变换后的点 仍在该直线上,
仍在该直线上,
∴ ,
,
得 ,
…(14分)
,
…(14分)
故所求直线为 ,取直线上一点
,取直线上一点 ,其经变换后得到的点
,其经变换后得到的点 仍在该直线上。
仍在该直线上。
∴ ,
…(16分)
,
…(16分)
即 ,得
,得 或
或 ,
,
故这样的直线存在,其方程为 或
或 ,
…(18分)
,
…(18分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com