
第六次月考试卷
一.选择题:
1.D2.C3.A4.A5.B6.A7.B8.C9.B10.C11. B12.C
二.选择题:
13.3 14.9π 15. -b 16.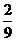
三.解答题:
17.(10分)解: ∵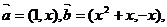 ∴
∴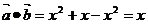 3分
3分
由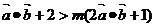 得,
得,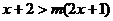 即
即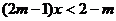
当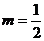 时,
时,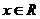 ; 6分 当
; 6分 当 时,
时,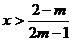 10分
10分
18.(12分)解:(Ⅰ)取PD的中点E,连接AE、EN∵EN平行且等于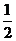 DC,而
DC,而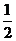 DC平行且等于AM ∴AMNE为平行四边形MN∥AE
DC平行且等于AM ∴AMNE为平行四边形MN∥AE
∴MN∥平面PAD (6分)
(Ⅱ)∵PA⊥平面ABCD∴CD⊥PA又∵ABCD为矩形∴CD⊥AD∴CD⊥AE,AE∥MN,MN⊥CD (3分)∵AD⊥DC,PD⊥DC ∴∠ADP=45°又E是斜边的PD的中点∴AE⊥PD,∴MN⊥PD∴MN⊥CD,∴MH⊥平面PCD.(6分)
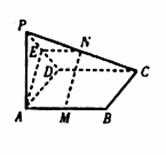
19.(12分)解:(1)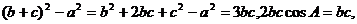
所以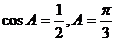 6分
6分
(2)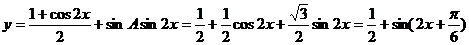
因为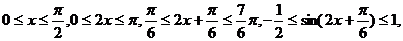
所以,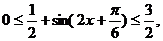 即
即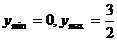
20.(12分) 解:(Ⅰ)由题意知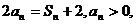
当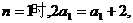
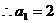 ……………………2分
……………………2分
当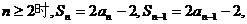
两式相减得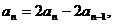 整理得:
整理得: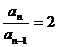 4分
4分
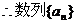 是以2为首项,2为公比的等比数列.
是以2为首项,2为公比的等比数列.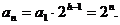 6分
6分
(Ⅱ)由(Ⅰ)知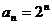
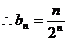 1分
1分
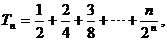 ①
①
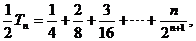 ②
②
①―②得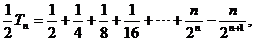 9分
9分
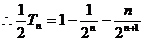 …4分
…4分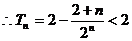 6分
6分
21.(12分)解:(1)由题有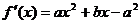 ,∵
,∵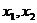 是
是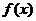 的两个极值点,∴
的两个极值点,∴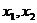 是方程
是方程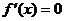 的两个实根,∵a>0,∴
的两个实根,∵a>0,∴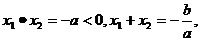
∴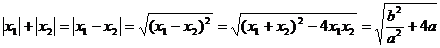
又∵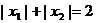 ,∴
,∴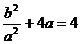 ,即
,即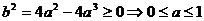 ; (6分)
; (6分)
(2)令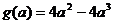 ,则
,则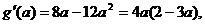 由
由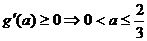 ,由
,由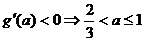 ,
,
故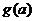 在
在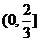 上是增函数,在区间
上是增函数,在区间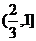 上是减函数, ∴
上是减函数, ∴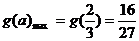 ,即
,即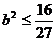 ,∴b的最大值是
,∴b的最大值是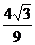 .
(6分)
.
(6分)
22.(12分).解:(1)抛物线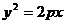 的准线
的准线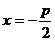 ,于是,4+
,于是,4+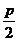 =5,∴p=2.
=5,∴p=2.
∴抛物线方程为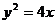 . (4分)
. (4分)
(2)∵点A的坐标是(4,4),由题意得B(0,4),M(0,2).又∵F(1,0), ∴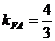 .又MN⊥FA,∴
.又MN⊥FA,∴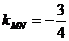 ,则FA的方程为
,则FA的方程为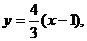 MN的方程为
MN的方程为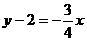 ,解方程组
,解方程组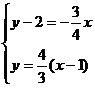 得,
得,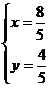 ∴N
∴N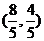 (4分)
(4分)
(3)由题意得,圆M的圆心是点(0,2),半径为2.
当m=4时,直线AK的方程为x=4,此时,直线AK与圆M相离.
当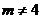 时,直线AK的方程为
时,直线AK的方程为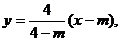 即为
即为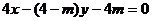 ,
,
圆心M(0,2)到直线AK的距离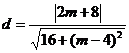 ,令d>2.解得m>1,
,令d>2.解得m>1,
所以,当m>1时,直线AK与圆M相离;当m=1时,直线AK与圆M相切,
当m<1时,直线AK与圆M相交. (4分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com