
北京市宣武区2008―2009学年度第二学期第一次质量检测
高 三 数 学(理) 2009.4
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共8页,全卷满分150分,考试时间为120分钟。
第I卷(选择题 共40分)
一、选择题(本大题共有8个小题,每小题5分,共40分;在每个小题给出的四个选项中,有且仅有一个是符合题目要求的)
1.已知集合 ,则
,则 等于
等于
A. B.
B.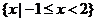 C.
C. D.
D.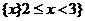
2.若 是空间两条不同的直线,
是空间两条不同的直线,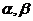 是空间的两个不同的平面,则
是空间的两个不同的平面,则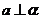 的一个充分不必要条件是
的一个充分不必要条件是
A.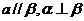 B.
B.
C. D.
D.
3.函数 的反函数是
的反函数是
A. B.
B.
C. D.
D.
4.已知两个向量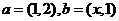 ,若
,若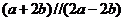 ,则
,则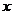 的值是
的值是
A.1 B. D.
D.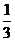
5.已知 满足条件
满足条件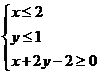 ,则
,则 的取值范围是
的取值范围是
A.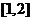 B.
B.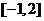 C.
C.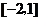 D.
D.
6.一次演出,原计划要排4个节目,因临时有变化,拟再添加2个小品节目,若保持原有4个节目的相对顺序不变,则这6个节目不同的排列方法有
A.30种 B.25种 C.24种 D.20种
7.已知 是等比数列,
是等比数列, 的取值范围是
的取值范围是
A.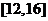 B.
B. C.
C.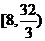 D.
D.
8.已知定义域是全体实数的函数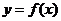 满足
满足 ,且函数
,且函数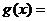
 ,函数
,函数 ,现定义函数
,现定义函数 为:
为: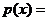
 其中
其中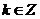
那么下列关于 叙述正确的是
叙述正确的是
A.都是奇函数且周期为 B.都是偶函数且周期为
B.都是偶函数且周期为
C.均无奇偶性但都有周期性 D.均无周期性但都有奇偶性
第Ⅱ卷(非选择题 共110分)
二、填空题(本大题共6个小题,每小题5分,共30分;把答案填在相应的位置上)
9.设i为虚数单位,则复数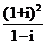 =___________。
=___________。
10.若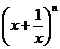 展开式的二项式系数之和为256,则
展开式的二项式系数之和为256,则 =_________,其展开式的常数项等于
=_________,其展开式的常数项等于
__________。(用数字作答)
11.在等差数列 中,已知
中,已知
12.设函数 的图象关于点
的图象关于点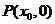 成中心对称,若
成中心对称,若 ,则
,则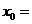 _______
_______
13.以双曲线 的离心率为半径,以右焦点为圆心的圆与该双曲线的渐近线相切,则
的离心率为半径,以右焦点为圆心的圆与该双曲线的渐近线相切,则 __________。
__________。
14.连结球面上两点的线段称为球的弦,半径为4的球的两条弦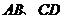 的长度分别为
的长度分别为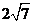 和
和 分别是
分别是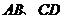 的中点,两条弦的两端都在球面上运动,有下面四个命题:
的中点,两条弦的两端都在球面上运动,有下面四个命题:
①弦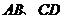 可能相交于点
可能相交于点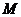 ;
;
②弦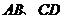 可能相交于点
可能相交于点 ;
;
③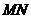 的最大值是5;
的最大值是5;
④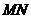 的最大值是1;
的最大值是1;
其中所有正确命题的序号为_______________。
三、解答题(本大题共6个大题,共80分;解答应写出必要的文字说明,证明过程及演算步骤)
15.(本题满分13分)
已知函数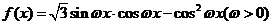 的最小正周期为
的最小正周期为 。
。
(1)求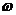 的值;
的值;
(2)设 的三边
的三边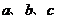 满足
满足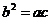 ,且边
,且边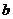 所对的角为
所对的角为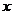 ,求此时
,求此时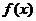 的值域
的值域
16.(本题满分13分)
将3封不同的信投进 这4个不同的信箱,假设每封信投入每个信箱的可能性相等
这4个不同的信箱,假设每封信投入每个信箱的可能性相等
(1)求这3封信分别被投进3个信箱的概率;
(2)求恰有2个信箱没有信的概率;
(3)求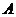 信箱中的信封数量的分布列和数学期望。
信箱中的信封数量的分布列和数学期望。
17.(本题满分13分)
如图,已知四棱锥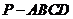 的底面的菱形,
的底面的菱形,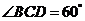 ,点
,点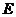 是
是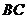 边的中点,
边的中点,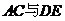 交于点
交于点 ,
,
(1)求证: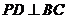 ;
;
(2)若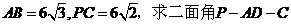 的大小;
的大小;
 (3)在(2)的条件下,求异面直线
(3)在(2)的条件下,求异面直线 与
与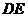 所成角的余弦值。
所成角的余弦值。
18.(本题满分13分)
设定义在R上的函数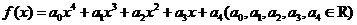
当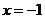 时
时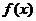 取得极大值
取得极大值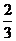 ,且函数
,且函数 的图象关于点
的图象关于点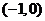 对称。
对称。
(1)求函数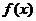 的表达式;
的表达式;
(2)试在函数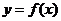 的图象上求两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在区间
的图象上求两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在区间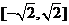 上;
上;
(3)设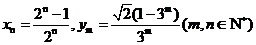 ,求证:
,求证: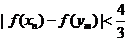 。
。
19.(本题满分14分)
已知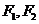 分别是椭圆
分别是椭圆 的左、右焦点,曲线
的左、右焦点,曲线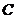 是以坐标原点为顶点,以
是以坐标原点为顶点,以 为焦点的抛物线,自点
为焦点的抛物线,自点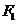 引直线交曲线
引直线交曲线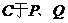 两个不同的交点,点
两个不同的交点,点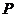 关于
关于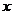 轴的对称点记为
轴的对称点记为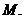 设
设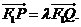
(1)求曲线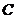 的方程;
的方程;
(2)证明: ;
;
(3)若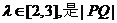 的取值范围。
的取值范围。
20.(本题满分14分)
已知数列 中,
中,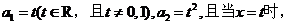
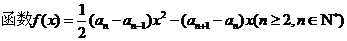 取得极值。
取得极值。
(1)求证:数列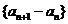 是等比数列;
是等比数列;
(2)若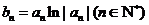 ,求数列
,求数列 的的前
的的前 项和
项和 ;
;
(3)当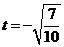 时,数列
时,数列 中是否存在最大项?如果存在,说明是第几项;如果不存在,请说明理由。
中是否存在最大项?如果存在,说明是第几项;如果不存在,请说明理由。
北京市宣武区2008―2009学年度第二学期第一次质量检测
一、选择题(本大题共有8个小题,每小题5分,共40分;在每个小题给出的四个选项中有且仅有一个符合题目要求的)
题号
1
2
3
4
5
6
7
8
答案
B
D
C
C
B
A
C
B
二、填空题(本大题共有6个小题,每小题5分,共30分;请把答案填在相应的位置)
题号
9
10
11
12
13
14
答案
-1+
8,70
24


①③④
三、解答题(本大题共6个小题,共80分;解答应写出文字说明,证明过程或演算步骤)
15.(本题满分13分)
解:(1)


(2)由题意,得

16.(本题满分13分)
解:(1)这3封信分别被投进3个信箱的概率为

(2)恰有2个信箱没有信的概率为

(3)设信箱 中的信箱数为
中的信箱数为


0
1
2
3





17.(本题满分13分)
解:解答一:(1)在菱形 中,连接
中,连接 则
则 是等边三角形。
是等边三角形。

(2)



(3)取 中点
中点 ,连结
,连结

解法二:(1)同解法一;
(2)过点 作
作 平行线交
平行线交 于
于 ,以点
,以点 为坐标原点,建立如图的坐标系
为坐标原点,建立如图的坐标系

 二面角
二面角 的大小为
的大小为
(3)由已知,可得点

即异面直线 所成角的余弦值为
所成角的余弦值为
18.(本题满分13分)
解:(1)将函数 的图象向右平移一个单位,得到函数
的图象向右平移一个单位,得到函数 的图象,
的图象,
 函数
函数 的图象关于点(0,0)对称,即函数
的图象关于点(0,0)对称,即函数 是奇函数,
是奇函数,


由题意得:
所以
(2)由(1)可得
故设所求两点为

 满足条件的两点的坐标为:
满足条件的两点的坐标为:
(3)


19.(本题满分14分)
解:(1)椭圆 的右焦点
的右焦点 的坐标为(1,0),
的坐标为(1,0),

(2)

(3)由(2)知

20.(本题满分14分)
解:(1)

(2)由(1)知

(3)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com