
桂林市2009届高三第二次调研考试题 姓名
数学(理 科)
一、选择题:(本大题共12小题;每小题5分.共60分)
1.设全集U={1,2,3,4,5},集合A={1,2},B={2,3},则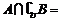 ( C )
( C )
A.{4,5} B.{2,3} C.{1} D.{2}
2.函数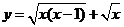 的定义域为( B )
的定义域为( B )
A.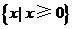 B.
B. C.
C. 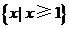 D.
D.
3.复数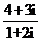 的实部是( B ) A.
的实部是( B ) A. B.
B. C.3 D.
C.3 D.
4.要得到一个奇函数,只需将函数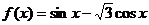 的图象( D )
的图象( D )
A.向右平移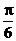 个单位 B.向右平移
个单位 B.向右平移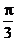 个单位 C.向左平移
个单位 C.向左平移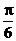 个单位 D.向左平移
个单位 D.向左平移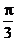 个单位
个单位
5.已知等差数列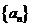 满足
满足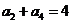 ,
,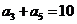 ,则它的前10项的和
,则它的前10项的和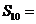 ( A )
( A )
A.95 B.
6.函数 的图像关于( C )
的图像关于( C )
A. 轴对称 B.直线
轴对称 B.直线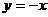 对称 C.坐标原点对称 D.直线
对称 C.坐标原点对称 D.直线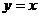 对称
对称
7.已知平面向量 ,
,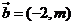 ,且
,且 //
//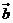 ,则
,则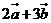 =( D )
=( D )
A.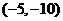 B.
B. C.
C.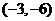 D.
D. 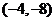
8.在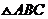 中,
中,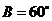 ,
,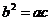 ,则
,则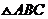 一定是 ( B )
一定是 ( B )
A. 等腰三角形 B. 等边三角形 C. 锐角三角形 D. 钝角三角形
9.设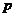 是椭圆
是椭圆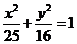 上的点.若
上的点.若 是椭圆的两个焦点,则
是椭圆的两个焦点,则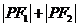 等于( A
)
等于( A
)
A.10 B.5 C.8 D. 4
10.双曲线的一条渐近线与实轴的夹角为α,则双曲线的离心率为 ( D )
A.sinα B. C.cosα D.
C.cosα D.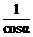
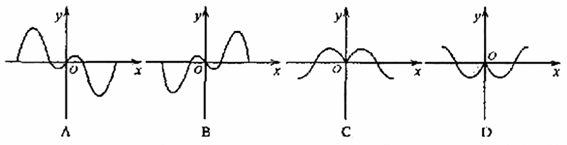
11.如果函数y=f(x)的图象如右图,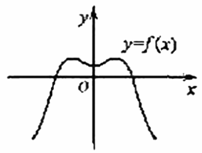
那么导函数y=f(x)的图象可能是 ( A )
12.已知点P 是抛物线 上一点,设点P到此抛物线准线的距离为
上一点,设点P到此抛物线准线的距离为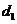 ,到直线
,到直线 的距离为
的距离为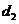 ,则
,则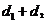 的最小值是 ( C
)
的最小值是 ( C
)
A. 5 B. 4 C. 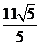 D.
D. 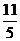
第II卷 (非选择题,共90分)
二、填空题:(本大题共4小题,每小题5分,共20分)
13.设变量 满足约束条件:
满足约束条件: ,则
,则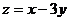 的最小值等于 -8 。
的最小值等于 -8 。
14.设函数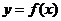 存在反函数
存在反函数 ,且函数
,且函数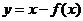 的图象过点(1,2),则函数
的图象过点(1,2),则函数 的图象一定过点 (-1,2) .
的图象一定过点 (-1,2) .
15.已知圆C: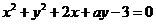 (a为实数)上任意一点关于直线l:
(a为实数)上任意一点关于直线l:
x-y+2=0的对称点都在圆C上,则a = -2 .
16.椭圆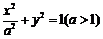 的一个焦点为F,点P在椭圆上,且
的一个焦点为F,点P在椭圆上,且 (O为坐标原点),则△OPF的面积S=
(O为坐标原点),则△OPF的面积S=  .
.
三、解答题:本大题共6小题,共70分.解答应给出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
已知函数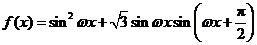 (
( )的最小正周期为
)的最小正周期为 .
.
(Ⅰ)求 的值;(Ⅱ)求函数
的值;(Ⅱ)求函数 在区间
在区间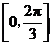 上的取值范围.
上的取值范围.
17.解:(Ⅰ)
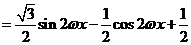
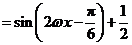 因为函数
因为函数 的最小正周期为
的最小正周期为 ,且
,且 ,所以
,所以 ,解得
,解得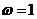 .
.
(Ⅱ)由(Ⅰ)得 因为
因为 ,
,
所以 , 所以
, 所以 ,
,
因此 ,即
,即 的取值范围为
的取值范围为 。。。。。。。。10分
。。。。。。。。10分
18. (本小题满分12分)
在 中,内角
中,内角 对边的边长分别是
对边的边长分别是 ,已知
,已知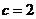 ,
, .
.
(Ⅰ)若 的面积等于
的面积等于 ,求
,求 ;(Ⅱ)若
;(Ⅱ)若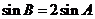 ,求
,求 的面积.
的面积.
18.解:(Ⅰ)由余弦定理得, ,
,
又因为 的面积等于
的面积等于 ,所以
,所以 ,得
,得 .???????????? 4分
.???????????? 4分
联立方程组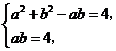 解得
解得 ,
,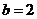 .?????????????????????????????????????? 6分
.?????????????????????????????????????? 6分
(Ⅱ)由正弦定理,已知条件化为 ,?????????????????????????????????????????????????????? 8分
,?????????????????????????????????????????????????????? 8分
联立方程组 解得
解得 ,
,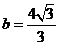 所以
所以 的面积
的面积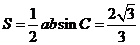
19.(本小题满分12分)
已知{an}是正数组成的数列,a1=1,且点( )(n
)(n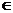 N*)在函数y=x2+1的图象上.
N*)在函数y=x2+1的图象上.
(Ⅰ)求数列{an}的通项公式;(Ⅱ)若列数{bn}满足b1=1,bn+1=bn+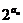 ,求证:bn
,求证:bn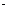 bn+2<b2n+1.
bn+2<b2n+1.
19.解: (Ⅰ)由已知得an+1=an+1、即an+1-an=1, ……………………2分
又a1=1,所以数列{an}是以1为首项,公差为1的等差数列.故an=1+(a-1)×1=n.
(Ⅱ) 由(Ⅰ)知:an=n从而bn+1-bn=2n.
bn=(bn-bn-1)+(bn-1-bn-2)+???+(b2-b1)+b1=2n-1+2n-2+???+2+1=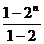
因为bn?bn+2-b =(2n-1)(2n+2-1)-(2n-1-1)2=(22n+2-2n+2-2n+1)-(22n+2-2-2n+1-1)=-5?2n+4?2n=-2n<0,
=(2n-1)(2n+2-1)-(2n-1-1)2=(22n+2-2n+2-2n+1)-(22n+2-2-2n+1-1)=-5?2n+4?2n=-2n<0,
所以bn?bn+2<b , ……………12分
, ……………12分
解法二:(Ⅰ)同解法一.
(Ⅱ)因为b2=1, bn+2- b =(bn+1-2n)(bn+1+2n+1)-
b
=(bn+1-2n)(bn+1+2n+1)-
b =2n+1?bn-1-2n?bn+1-2n?2n+1=2n(bn+1-2n+1)
=2n+1?bn-1-2n?bn+1-2n?2n+1=2n(bn+1-2n+1)
=2n(bn+2n-2n+1)=2n(bn-2n)=…=2n(b1-2)=-2n〈0,所以bn-bn+2<b2n+1
20. (本小题满分12分)
在实数集R上定义运算 若
若 ,
,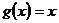 ,若
,若 .
.
(Ⅰ) 求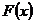 的解析式; (Ⅱ) 若
的解析式; (Ⅱ) 若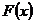 单在
单在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
(Ⅲ) 若 ,
,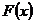 的曲线上是否存在两点,使得过这两点的切线互相垂直,若存在,求出切线方程;若不存在,说明理由.
的曲线上是否存在两点,使得过这两点的切线互相垂直,若存在,求出切线方程;若不存在,说明理由.
20.解:(Ⅰ)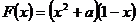 =
= 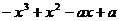 ………………2分
………………2分
(Ⅱ)∵ 当
当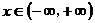 上时,
上时,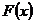 单调递减
单调递减
∴ 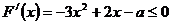 ,
,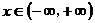 恒成立 ……………6分
恒成立 ……………6分
∴△=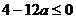 解得:
解得: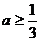 …………7分
…………7分
(Ⅲ)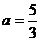 时,
时,
 是
是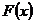 曲线上的任意两点
曲线上的任意两点
∵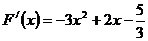
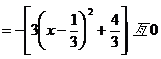 ………………9分
………………9分
∴ ∴
∴ 不成立 ∴
不成立 ∴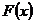 的曲线上不存在两点,使得过这两点的切线互相垂直。
的曲线上不存在两点,使得过这两点的切线互相垂直。
21.(本小题满分12分)
已知函数
(1)若函数 在(
在(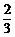 ,1)上单调递减,在(1,+∞)上单调递增,求实数a的值;
,1)上单调递减,在(1,+∞)上单调递增,求实数a的值;
(2)是否存在正整数a,使得 在(
在(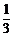 ,
, )上既不是单调递增函数也不是单调递减函数?若存在,试求出a的值,若不存在,请说明理由.
)上既不是单调递增函数也不是单调递减函数?若存在,试求出a的值,若不存在,请说明理由.
21.解:(1)∵ 在(
在(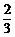 ,1)上单调递减,在(1,+∞)上单调递增,
,1)上单调递减,在(1,+∞)上单调递增,
又
 =3x2+2ax-2 ∴
=3x2+2ax-2 ∴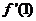 =0,∴a=-
=0,∴a=- .
.
(2)令 =3x2+2ax-2=0.4a2+24>0,∴方程有两个实根分别记为x1,x2.
=3x2+2ax-2=0.4a2+24>0,∴方程有两个实根分别记为x1,x2.
由于x1?x2=-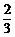 ,说明x1,x2一正一负,即在(
,说明x1,x2一正一负,即在(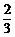 ,1)内方程
,1)内方程 =0不可能有两个解。
=0不可能有两个解。
故要使得 在(
在(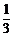 ,
, )上既不是单调增函数也不是单调减函数的充要条件是
)上既不是单调增函数也不是单调减函数的充要条件是
 (
(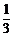 )
)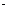
 (
( )<0 即(
)<0 即(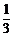 +
+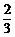 a-2)(
a-2)( +a-2)<0 解得
+a-2)<0 解得
∵a是正整数 ∴a=2 ……………………12分
22.(本小题满分12分)
已知椭圆 的方程为
的方程为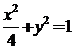 ,双曲线
,双曲线 的左、右焦点分别是
的左、右焦点分别是 的左、右顶点,而
的左、右顶点,而 的左、右顶点分别是
的左、右顶点分别是 的左、右焦点。
的左、右焦点。
(1)求双曲线 的方程;
的方程;
(2)若直线 与双曲线C2恒有两个不同的交点A和B,且
与双曲线C2恒有两个不同的交点A和B,且 (其中O为原点),求
(其中O为原点),求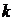 的范围。
的范围。
22.解:解:(1)设双曲线 的方程为
的方程为 则
则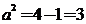 ,再由
,再由 得
得
故 的方程为
的方程为 ……………………… 3分
……………………… 3分
(2)将 代入
代入 得
得 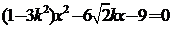
由直线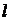 与双曲线C2交于不同的两点得:
与双曲线C2交于不同的两点得:
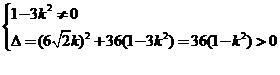
 且
且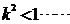 ①
①
设 ,则
,则
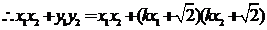

又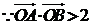 ,得
,得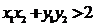
 即
即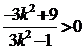 ,解得:
,解得: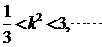 ②
②
由①、②得: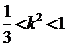 故k的取值范围为
故k的取值范围为 ………………………12分
………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com