
安徽省蚌埠市2009届高三年级第一次教学质量检查考试
数 学(文科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间为120分钟
第Ⅰ卷(选择题,共60分)
一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的,)
1、已知全集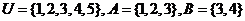 ,则
,则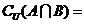
A、{3} B、{4,5} C、{1,2,4,5} D、{1,2,3,4}
2、已知函数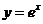 的图像与函数
的图像与函数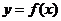 的图像关于直线
的图像关于直线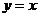
对称,则
A、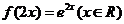 B、
B、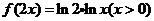
C、 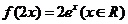 D、
D、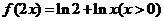
3、设函数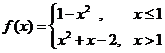 ,则
,则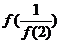 等于
等于
A、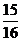 B、
B、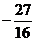 C、
C、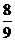 D、18
D、18
4、已知直线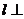 平面
平面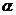 ,直线
,直线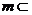 平面
平面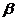 ,给出下列命题:①
,给出下列命题:①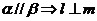 ;②
;②
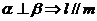 ;③
;③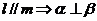 ;④
;④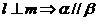 ,其中正确命题的序号是
,其中正确命题的序号是
A、①②③ B、②③④ C、②④ D、①③
5、已知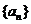 是等比数列,
是等比数列,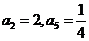 ,则
,则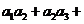 …
…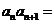
A、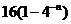 B、
B、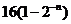 C、
C、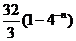 D、
D、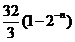
6、设命题p:命题“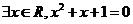 ”的否定是“
”的否定是“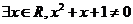 ”;命题
”;命题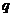 :
:
“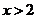 ”是“
”是“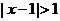 ”的充分不必要条件,则
”的充分不必要条件,则
A、“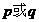 ”为真 B、“
”为真 B、“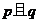 ”为真 C、
”为真 C、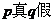 D、
D、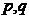 均为假命题
均为假命题
7、已知平面向量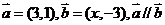 ,则x等于
,则x等于
A、9 B、
8、已知函数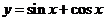 ,给出以下四个命题,其中为真命题的是
,给出以下四个命题,其中为真命题的是
A、若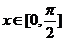 ,则
,则 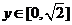 B、在区间
B、在区间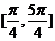 上是增函数
上是增函数
C、直线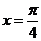 是函数图象的一条对称轴
是函数图象的一条对称轴
D、函数的图象可由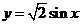 的图象向右平移
的图象向右平移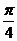 个单位得到
个单位得到
9、设F 是椭圆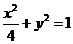 的右焦点,椭圆上的点与点F 的最大距离为M,最小距离为m,则椭圆上与点F的距离等于
的右焦点,椭圆上的点与点F 的最大距离为M,最小距离为m,则椭圆上与点F的距离等于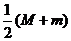 的点的坐标是
的点的坐标是
A、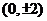 B、
B、 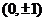 C、
C、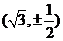 D、
D、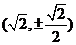
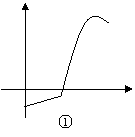
10、已知图中一组函数图象,它们分别与其后所列的一个现实情境相匹配:
 |
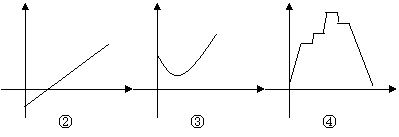 |
情境A:一份30分钟前从冰箱里取出来,然后被防到微波炉里加热,最后放到餐桌上的食物的温度(将0时刻确定为食物从冰箱里被取出来的那一刻)
情境B:一个1970年生产的留声机从它刚开始的售价到现在的价值(它被一个爱好者收藏,并且被保存的很好);
情境C:从你刚开始防水洗澡,到你洗完后把它排掉这段时间浴缸里水的高度;
情境D:根据乘客人数,每辆公交车一趟营运的利润。
其中与情境A、B、、C、D对应的图象正确的序号是
 11、已知直线
11、已知直线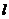 的斜率为―1,且过定点(1,
的斜率为―1,且过定点(1,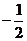 ),点
),点
P(x,y)为直线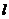 位于第一象限的任意一点,则
位于第一象限的任意一点,则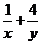
的最小值是
A、8 B、
12、如图是一个由三根细棒PA、PB、PC组成的支架,
三根细棒PA、PB、PC两两所成的角都为600,一个半
径为1的小球放在支架上,则球心O到点P 的距离是
A、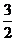 B、
B、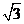 D、
D、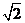
二、填空题:本大题共4个小题,每小题4分,共16分,请将答案直接填在题中横线上。
13、已知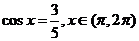 ,则
,则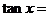 _____
_____
14、曲线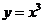 相切于点(1,1)的切线方程是_____.
相切于点(1,1)的切线方程是_____.
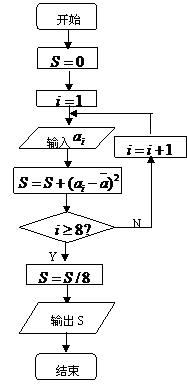 15、已知M、N是
15、已知M、N是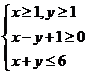 所围成的区域内的不同两点,则|MN|的最大值______________。
所围成的区域内的不同两点,则|MN|的最大值______________。
16、对一个作直线运动的质点的运动过程观
测了8次,得到如下表所示的数据:
观测次数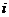
1
2
3
4
5
6
7
8
观测数据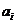
40
41
43
43
44
46
47
48
在上述统计数据的分析中,一部分计算机如图所示的算法
流程图(其中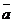 是这8个数据的平均数),则输出的S的值
是这8个数据的平均数),则输出的S的值
是____________________。
、证明过程和演算步骤。
三、解答题:本大题共6个小题,共74分,解答须写出说明
17、(本小题12分)设△ABC的内角A、B、C所对的边长
分别为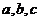 ,若
,若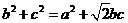
(1)求A的大小;
(2)求 的值。
的值。
周销售量(单位:吨)
2
3
4
频数
20
50
30
18、(本小题12分)将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为a,第二次出现的点数为b,设复数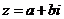
(1) 求事件“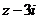 为实数”的概率;
为实数”的概率;
(2)求事件“|z―2|≤
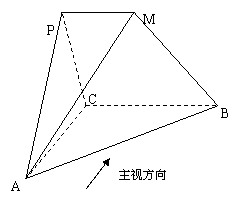 19、(本小题12分)如图所示几何体中,平面PAC⊥平面ABC,批PM//BC,PA=PC,AC=1,BC=2PM=2,AB=
19、(本小题12分)如图所示几何体中,平面PAC⊥平面ABC,批PM//BC,PA=PC,AC=1,BC=2PM=2,AB=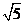 ,若该几何体左试图(侧视图)的面积为
,若该几何体左试图(侧视图)的面积为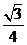
(1)求证:PA⊥BC;
(2)画出该几何体的主试图并求其面积S;
(3)求多面体PMABC的体积V
20、(本小题12分)已知函数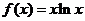
(1)求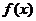 的最小值;
的最小值;
(2)若对所有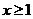 都有
都有 求实数
求实数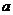 的取值范围。
的取值范围。
21、(本小题12分)已知曲线C上任意一点P到直线x=1与点F(―1,0)的距离相等。
(1)求曲线C的方程;
(2)设直线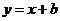 与曲线C交于点A、B,问在直线
与曲线C交于点A、B,问在直线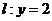 上是否存在于b无关的定点M,使得直线MA,MB关于直线
上是否存在于b无关的定点M,使得直线MA,MB关于直线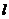 对称,若存在,求出点M的坐标,若不存在,请说明理由。
对称,若存在,求出点M的坐标,若不存在,请说明理由。
22、(本小题14分)已知函数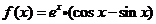 将函数
将函数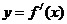 的所有正零点x从小到大排成数列
的所有正零点x从小到大排成数列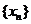 ,记
,记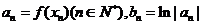
(1)证明:数列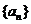 是等比数列;
是等比数列;
(2)求数列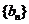 的前n项和;
的前n项和;
(3)若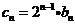 ,求数列
,求数列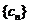 的前n项和
的前n项和
安徽省蚌埠市2009届高三年级第一次教学质量检查考试
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
D
A
D
C
A
D
C
B
D
B
C
二、填空题:
13、 14、
14、 15、
15、 等; 16、7
等; 16、7
三、解答题
17、(1)由余弦定理: 又
又
∴ ∴
∴
(2)∵A+B+C= ∴
∴
∴
18、(1) (2)
(2)
19、(1)AC=1,BC=2 ,AB= ,∴
,∴ ∴AC
∴AC
又 平面PAC 平面ABC,平面PAC
平面ABC,平面PAC 平面ABC=AC,∴BC
平面ABC=AC,∴BC 平面PAC
平面PAC
又∵PA 平面APC ∴
平面APC ∴
 (2)该几何体的主试图如下:
(2)该几何体的主试图如下:
几何体主试图的面积为
 ∴
∴ ∴
∴
(3)取PC 的中点N,连接AN,由△PAC是边长为1的正三角形,可知
由(1)BC 平面PAC,可知
平面PAC,可知 ∴
∴ 平面PCBM
平面PCBM
∴
20、(1) 的最小值为
的最小值为
(2)a的取值范围是
21、(1)曲线C的方程为
(2) ,存在点M(―1,2)满足题意
,存在点M(―1,2)满足题意
22、(1)由于点B1(1,y1),B2(2,y2),…,Bn(n,yn)( )在直线
)在直线 上
上
则 因此
因此 ,所以
,所以 是等差数列
是等差数列
(2)由已知有 得
得 同理
同理 
∴
∴

∴
(3)由(2)得 ,则
,则

∴
∴
∴
由于 而
而
则
 ,从而
,从而
同理: ……
…… 
以上 个不等式相加得:
个不等式相加得:
即 ,从而
,从而

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com