2,4,6 A.三角形 B.四边形 C.五边形 D.六边形
试题详情
3.已知 是公比为2的等比数列,则 是公比为2的等比数列,则 的值为
( ) 的值为
( ) 试题详情
试题详情
4.吉林省生物制品厂生产了一批药品,它们来自甲、乙、丙三条生产线,其中来自甲生产线1000件,来自乙生产线2000件,来自丙生产线3000件,现采用分层抽样的方法对这批药品进行抽样检测,抽取的样品数为24件.则从乙生产线抽取的样品数是 ( ) A.4件 B.6件 C.8件 D.12件 试题详情
5. 给出下面的三个命题:①函数 的最小正周期是 的最小正周期是 ②函数 ②函数 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
8.设函数 ,下列结论中正确的是
( ) ,下列结论中正确的是
( ) 试题详情
试题详情
试题详情
试题详情
D.函数 无极值 无极值 试题详情
试题详情
10. 已知对称轴为坐标轴的双曲线的两条渐近线方程为 ,若双曲线上有一点 ,若双曲线上有一点 ,使 ,使 ,则双曲线焦点 ( ) ,则双曲线焦点 ( ) A.在x轴上 B.在y轴上 试题详情
C.当 时,在x轴上 D.当 时,在x轴上 D.当 时,在y轴上 时,在y轴上 试题详情
11. 已知 ,则在数列{an}的前50项中最小项和最大项分别是 (
) ,则在数列{an}的前50项中最小项和最大项分别是 (
) 试题详情
试题详情
12.若函数 在区间 在区间 内单调递增,则a的取值范围是 ( ) 内单调递增,则a的取值范围是 ( ) 试题详情
A. B. B. C. C. D. D.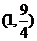 第Ⅱ卷(非选择题,共90分) 试题详情
二、填空题:本大题共4小题,每小题5分,共20分.把答案填写在答题纸相应位置上. 13.二项式 的展开式中的常数项为_____________(用数字作答). 的展开式中的常数项为_____________(用数字作答). 试题详情
试题详情
15.已知函数 ,则 ,则 __________. __________. 试题详情
16.设函数 ,给出下列4个命题: ,给出下列4个命题: 试题详情
试题详情
③ 的图象关于点 的图象关于点 对称; ④方程 对称; ④方程 至多有2个实数根 至多有2个实数根 上述命题中的所有正确命题的序号是
. 试题详情
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
试题详情
在△ABC中,a,b,c分别为角A,B,C所对的三边,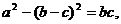 (Ⅰ)求角A; 试题详情
(Ⅱ)若BC=2 ,角B等于x,周长为y,求函数 ,角B等于x,周长为y,求函数 的取值范围. 的取值范围. 试题详情
18.(本题满分12分) 从“神七”飞船带回的某种植物种子由于在太空中被辐射,我们把它们称作“太空种子”. 这种“太空种子”成功发芽的概率为 ,发生基因突变的概率为 ,种子发芽与发生基因突变是两个相互独立事件.科学家在实验室对“太空种子”进行培育,从中选出优良品种. (Ⅰ)这种“太空种子”中的某一粒种子既发芽又发生基因突变的概率是多少? (Ⅱ)四粒这种“太空种子”中至少有两粒既发芽又发生基因突变的概率是多少? 试题详情
试题详情
已知函数 试题详情
试题详情
试题详情
试题详情
如图,已知在直四棱柱 中, 中, 试题详情
试题详情
(I)求证: 平面 平面 ; ; 试题详情
(II)求二面角 的余弦值. 的余弦值. 试题详情
试题详情
试题详情
(Ⅰ)当 时,求函数 时,求函数 的极值和单调递增区间; 的极值和单调递增区间; 试题详情
(Ⅱ)求证: . . 试题详情
试题详情
试题详情
试题详情
1.B 2 D. 3.B 4.C 5.C 6.C 7.B 8.C 9.D 10.B 11.D 12.B 13.240 14.1 15. 16.
①②③ 16.
①②③ 17.(本题满分10分) 解:(Ⅰ)由  又 又 
(Ⅱ)  同理: 
 
故 , , , , . . 18.(本题满分12分) 解:(Ⅰ)记“这批太空种子中的某一粒种子既发芽又发生基因突变”为事件 ,则 ,则 . . (Ⅱ)  19.(本题满分12分) 解 (Ⅰ)∵ (Ⅰ)∵ ,∴{ ,∴{ }是公差为4的等差数列, }是公差为4的等差数列, ∵a1=1,  = = +4(n-1)=4n-3,∵an>0,∴an= +4(n-1)=4n-3,∵an>0,∴an= (Ⅱ)bn=Sn+1-Sn=an+12= ,由bn< ,由bn< ,得m> ,得m> , , 设g(n)=  ,∵g(n)= ,∵g(n)=  在n∈N*上是减函数, 在n∈N*上是减函数, ∴g(n)的最大值是g(1)=5, ∴m>5,存在最小正整数m=6,使对任意n∈N*有bn< 成立 成立 20.(本题满分12分) 解法一: (I)设 是 是 的中点,连结 的中点,连结 ,则四边形 ,则四边形 为正方形, 为正方形,  .故 .故 , , , , , , ,即 ,即 . .
 又 又 , ,
 平面 平面 , ,
(II)由(I)知 平面 平面 , , 又 平面 平面 , , , , 取 的中点 的中点 , 连结 , 连结 ,又 ,又 ,则 ,则 . . 取 的中点 的中点 ,连结 ,连结 ,则 ,则 , , . .  为二面角 为二面角 的平面角. 的平面角.
连结 ,在 ,在 中, 中, , , , , 取 的中点 的中点 ,连结 ,连结 , , , , 在 中, 中, , , , , . .  . .
 二面角 二面角 的余弦值为 的余弦值为 . .
解法二: (I)以 为原点, 为原点, 所在直线分别为 所在直线分别为 轴, 轴, 轴, 轴, 轴建立如图所示的空间直角坐标系,则 轴建立如图所示的空间直角坐标系,则 , , , , , , , , , , . .   , , , ,


又因为 所以, 所以, 平面 平面 . . (II)设 为平面 为平面 的一个法向量. 的一个法向量. 由 , , , ,  得 取 取 ,则 ,则 . . 又 , , ,设 ,设 为平面 为平面 的一个法向量, 的一个法向量, 由 , , ,得 ,得 取 取 ,则 ,则 , , 设 与 与 的夹角为 的夹角为 ,二面角 ,二面角 为 为 ,显然 ,显然 为锐角, 为锐角,  , ,
21.(本题满分12分) 解:(Ⅰ)  , , 在 在 上是增函数,在 上是增函数,在 上是减函数, 上是减函数, ∴当 时, 时,  取得极大值. 取得极大值. ∴ 即 即 . . 由 , , 得 得 , , 则有  , , 












递增 极大值4 递减 极小值0 递增 所以, 当 时,函数 时,函数 的极大值为4;极小值为0; 单调递增区间为 的极大值为4;极小值为0; 单调递增区间为 和 和 . . (Ⅱ) 由(Ⅰ)知 , ,  , , 的两个根分别为 的两个根分别为 . ∵ . ∵ 在 在 上是减函数,∴ 上是减函数,∴ ,即 ,即 , ,  . .
22.(本题满分12分) 解:(I)依题意,可知 , , ∴  ,解得 ,解得 ∴椭圆的方程为 (II)直线 : : 与⊙ 与⊙ 相切,则 相切,则 ,即 ,即 , , 由 ,得 ,得 , , ∵直线 与椭圆交于不同的两点 与椭圆交于不同的两点 设 设 ∴ , , 
 , ,
∴ ∴ ∴
∴ , , ∴  设 ,则 ,则 , , ∵ 在 在 上单调递增
∴ 上单调递增
∴ . .
| 
 ,则
,则  ( )
( ) D.
D.
 中,
中, 、
、 、
、 分别是
分别是 、
、 、
、 的中点.那么,正
的中点.那么,正