
题目列表(包括答案和解析)
53、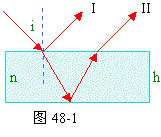 如图48-1所示,折射率为n的玻璃砖的两面是平行的,玻璃砖厚度为h,一束细光束射到玻璃砖上表面的入射角为i,光线一部分从上表面反射回空气中;另一部分折射入玻璃砖,在玻璃砖下表面发生反射,又在上表面折射后射入空气中。求:上表面的反射光线I与下表面反射,折射回到空气的光线II的侧移距离为多少?
如图48-1所示,折射率为n的玻璃砖的两面是平行的,玻璃砖厚度为h,一束细光束射到玻璃砖上表面的入射角为i,光线一部分从上表面反射回空气中;另一部分折射入玻璃砖,在玻璃砖下表面发生反射,又在上表面折射后射入空气中。求:上表面的反射光线I与下表面反射,折射回到空气的光线II的侧移距离为多少?
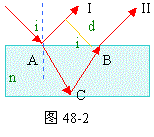 分析与解:光路图如图48-2所示。光线射到A点,反射光线为I,折射光线射到下表面C点再反射到上表面B点,形成折射光线II。
分析与解:光路图如图48-2所示。光线射到A点,反射光线为I,折射光线射到下表面C点再反射到上表面B点,形成折射光线II。
由折射定律知: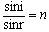 [1]
[1]
由图知:AB=2htgr [2]
光线Ⅱ相对I的侧移距离d为:d=ABcosi [3]
 联立解[1][2][3]式得:d=
联立解[1][2][3]式得:d=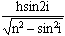
12、质量为m的钢板与直立轻弹簧的上端连接,弹簧下端固定在地上。平衡时,弹簧的压缩量为Xo,如图11-1所示。一物块从钢板正上方距离为 3Xo的A处自由落下,打在钢板上并立刻与钢板一起向下运动,但不粘连。它们到达最低点后又向上运动。已知物块质量也为m时,它们恰能回到O点。若物块质量为2m,仍从A处自由落下,则物块与钢板回到O点时,还具有向上的速度。求物块向上运动到达的最高点O点的距离。
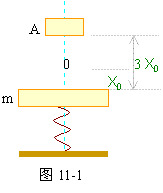 分析与解:物块自由下落,与钢板碰撞,压缩弹簧后再反弹向上,运动到O点,弹簧恢复原长。碰撞过程满足动量守恒条件。压缩弹簧及反弹时机械能守恒。自由下落3Xo,根据机械能守恒:
分析与解:物块自由下落,与钢板碰撞,压缩弹簧后再反弹向上,运动到O点,弹簧恢复原长。碰撞过程满足动量守恒条件。压缩弹簧及反弹时机械能守恒。自由下落3Xo,根据机械能守恒:
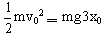 所以
所以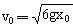 物块与钢板碰撞时,根据动量守恒: mv0=(m+m)v1(v1为碰后共同速度)
物块与钢板碰撞时,根据动量守恒: mv0=(m+m)v1(v1为碰后共同速度)
V1=V0/2=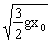
物块与钢板一起升到O点,根据机械能守恒: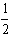 2mV12+Ep=2mgx0
[1]
2mV12+Ep=2mgx0
[1]
如果物块质量为2m,则:2mVo=(2m+m)V2
,即V2=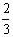 Vo
Vo
设回到O点时物块和钢板的速度为V,则: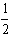 3mV22+Ep=3mgx0+
3mV22+Ep=3mgx0+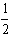 3mV2
[2]
3mV2
[2]
从O点开始物块和钢板分离,由[1]式得:
Ep=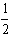 mgx0
代入[2]得:
mgx0
代入[2]得: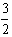 m(
m(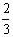 Vo)2+
Vo)2+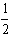 mgx0=3mgx0+
mgx0=3mgx0+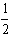 3mV2
3mV2
所以,V2=gx0
即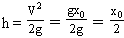 (未完待续)
(未完待续)
11、如图10-1所示,劲度系数为 K的轻质弹簧一端与墙固定,另一端与倾角为θ的斜面体小车连接,小车置于光滑水平面上。在小车上叠放一个物体,已知小车质量为 M,物体质量为m,小车位于O点时,整个系统处于平衡状态。现将小车从O点拉到B点,令OB=b,无初速释放后,小车即在水平面B、C间来回运动,而物体和小车之间始终没有相对运动。求:(1)小车运动到B点时的加速度大小和物体所受到的摩擦力大小。(2)b的大小必须满足什么条件,才能使小车和物体一起运动过程中,在某一位置时,物体和小车之间的摩擦力为零。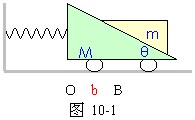
分析与解:
(1)所求的加速度a和摩擦力f是小车在B点时的瞬时值。取M、m和弹簧组成的系统为研究对象,由牛顿第二定律:kb=(M+m)a 所以a=kb/(M+m)。
取m为研究对象,在沿斜面方向有:f-mgsinθ=macosθ
所以,f=mgsinθ+m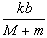 cosθ=m(gsinθ+
cosθ=m(gsinθ+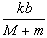 cosθ)
cosθ)
(2)当物体和小车之间的摩擦力的零时,小车的加速度变为a’,小车距O点距离为b’,取m为研究对象,有:mgsinθ=ma’cosθ
取M、m和弹簧组成的系统为研究对象,有:kb‘=(M+m)a’
以上述两式联立解得:b‘=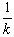 (M+m)gtgθ
(M+m)gtgθ
说明:在求解加速度时用整体法,在分析求解m受到的摩擦力时用隔离法。整体法和隔离法两者交互运用是解题中常用的方法,希读者认真掌握。
10、如图9-1所示,质量为M=3kg的木板静止在光滑水平面上,板的右端放一质量为m=1kg的小铁块,现给铁块一个水平向左速度V0=4m/s,铁块在木板上滑行,与固定在木板左端的水平轻弹簧相碰后又返回,且恰好停在木板右端,求铁块与弹簧相碰过程中,弹性势能的最大值EP。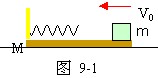
分析与解:在铁块运动的整个过程中,系统的动量守恒,因此弹簧压缩最大时和铁块停在木板右端时系统的共同速度(铁块与木板的速度相同)可用动量守恒定律求出。在铁块相对于木板往返运动过程中,系统总机械能损失等于摩擦力和相对运动距离的乘积,可利用能量关系分别对两过程列方程解出结果。
设弹簧压缩量最大时和铁块停在木板右端时系统速度分别为V和V’,由动量守恒得:mV0=(M+m)V=(M+m)V’ 所以,V=V’=mV0/(M+m)=1X4/(3+1)=1m/s
铁块刚在木板上运动时系统总动能为:EK=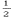 mV02=0.5X1X16=8J
mV02=0.5X1X16=8J
弹簧压缩量最大时和铁块最后停在木板右端时,系统总动能都为:
EK’=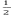 (M+m)V2=0.5X(3+1)X1=2J
(M+m)V2=0.5X(3+1)X1=2J
铁块在相对于木板往返运过程中,克服摩擦力f所做的功为:
Wf=f2L=EK-EK’=8-2=6J
铁块由开始运动到弹簧压缩量最大的过程中,系统机械能损失为:fs=3J
由能量关系得出弹性势能最大值为:EP=EK-EK‘-fs=8-2-3=3J
说明:由于木板在水平光滑平面上运动,整个系统动量守恒,题中所求的是弹簧的最大弹性势能,解题时必须要用到能量关系。在解本题时要注意两个方面:①.是要知道只有当铁块和木板相对静止时(即速度相同时),弹簧的弹性势能才最大;弹性势能量大时,铁块和木板的速度都不为零;铁块停在木板右端时,系统速度也不为零。
②.是系统机械能损失并不等于铁块克服摩擦力所做的功,而等于铁块克服摩擦力所做的功和摩擦力对木板所做功的差值,故在计算中用摩擦力乘上铁块在木板上相对滑动的距离。
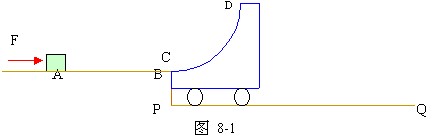
9、如图8-1所示,质量为m=0.4kg的滑块,在水平外力F作用下,在光滑水平面上从A点由静止开始向B点运动,到达B点时外力F突然撤去,滑块随即冲上半径为 R=0.4米的1/4光滑圆弧面小车,小车立即沿光滑水平面PQ运动。设:开始时平面AB与圆弧CD相切,A、B、C三点在同一水平线上,令AB连线为X轴,且AB=d=0.64m,滑块在AB面上运动时,其动量随位移的变化关系为P=1.6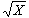 kgm/s,小车质量M=3.6kg,不计能量损失。求:
kgm/s,小车质量M=3.6kg,不计能量损失。求:
(1)滑块受水平推力F为多大? (2)滑块通过C点时,圆弧C点受到压力为多大? (3)滑块到达D点时,小车速度为多大? (4)滑块能否第二次通过C点? 若滑块第二次通过C点时,小车与滑块的速度分别为多大? (5)滑块从D点滑出再返回D点这一过程中,小车移动距离为多少? (g取10m/s2)
分析与解:(1)由P=1.6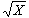 =mv,代入x=0.64m,可得滑块到B点速度为:
=mv,代入x=0.64m,可得滑块到B点速度为:
VB=1.6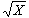 /m=1.6
/m=1.6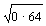 =3.2m/s
=3.2m/s
A→B,由动能定理得:FS=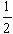 mVB2
mVB2
所以 F=mVB2/(2S)=0.4X3.22/(2X0.64)=3.2N
(2)滑块滑上C立即做圆周运动,由牛顿第二定律得:
N-mg=mVC2/R 而VC=VB 则 N=mg+mVC2/R=0.4X10+0.4X3.22/0.4=14.2N
(3)滑块由C→D的过程中,滑块和小车组成系统在水平方向动量守恒,由于滑块始终紧贴着小车一起运动,在D点时,滑块和小车具有相同的水平速度VDX 。由动量守恒定律得:mVC=(M+m)VDX
所以 VDX=mVC/(M+m)=0.4X3.2/(3.6+0.4)=0.32m/s
(4)滑块一定能再次通过C点。因为滑块到达D点时,除与小车有相同的水平速度VDX外,还具有竖直向上的分速度VDY,因此滑块以后将脱离小车相对于小车做竖直上抛运动(相对地面做斜上抛运动)。因题中说明无能量损失,可知滑块在离车后一段时间内,始终处于D点的正上方(因两者在水平方向不受力作用,水平方向分运动为匀速运动,具有相同水平速度), 所以滑块返回时必重新落在小车的D点上,然后再圆孤下滑,最后由C点离开小车,做平抛运动落到地面上。由机械能守恒定律得:
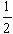 mVC2=mgR+
mVC2=mgR+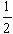 (M+m)VDX2+
(M+m)VDX2+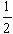 mVDY2
mVDY2
所以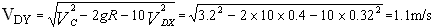
以滑块、小车为系统,以滑块滑上C点为初态,滑块第二次滑到C点时为末态,此过程中系统水平方向动量守恒,系统机械能守恒(注意:对滑块来说,此过程中弹力与速度不垂直,弹力做功,机械能不守恒)得:
mVC=mVC‘+MV 即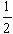 mVC2=
mVC2=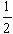 mVC’2+
mVC’2+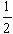 MV2
MV2
上式中VC‘、V分别为滑块返回C点时,滑块与小车的速度,
V=2mVC/(M+m)=2X0.4X3.2/(3.6+0.4)=0.64m/s
VC’=(m-M)VC/(m+M)=(0.4-3.6)X3.2/(0.4+3.6)=-2.56m/s(与V反向)
(5)滑块离D到返回D这一过程中,小车做匀速直线运动,前进距离为:
△S=VDX2VDY/g=0.32X2X1.1/10=0.07m
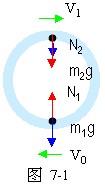
8、一内壁光滑的环形细圆管,位于竖直平面内,环的半径为R(比细管的内径大得多。在圆管中有两个直径与细管内径相同的小球(可视为质点)。A球的质量为m1,B球的质量为m2。它们沿环形圆管顺时针运动,经过最低点时的速度都为V0。设A球运动到最低点时,B球恰好运动到最高点,若要此时两球作用于圆管的合力为零,那么m1、m2、R与V0应满足的关系式是 。
分析与解:如图7-1所示,A球运动到最低点时速度为V0,A球受到向下重力mg和细管向上弹力N1的作用,其合力提供向心力。那么,N1-m1g=m1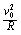 [1]
[1]
这时B球位于最高点,速度为V1,B球受向下重力m2g和细管弹力N2作用。球作用于细管的力是N1、N2的反作用力,要求两球作用于细管的合力为零,即要求N2与N1等值反向,N1=N2 [2],
且N2方向一定向下,对B球:N2+m2g=m2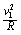 [3]
[3]
B球由最高点运动到最低点时速度为V0,此过程中机械能守恒:
即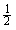 m2V12+m2g2R=
m2V12+m2g2R=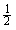 m2V02
[4]
m2V02
[4]
由[1][2][3][4]式消去N1、N2和V1后得到m1、m2、R与V0满足的关系式是:
(m1-m2)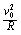 +(m1+5m2)g=0
[5]
+(m1+5m2)g=0
[5]
说明:(1)本题不要求出某一物理量,而是要求根据对两球运动的分析和受力的分析,在建立[1]-[4]式的基础上得到m1、m2、R与V0所满足的关系式[5]。(2)由题意要求两球对圆管的合力为零知,N2一定与N1方向相反,这一点是列出[3]式的关键。且由[5]式知两球质量关系m1<m2。
1]、[2]两式消去GM解得:V=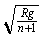 =
=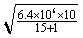 =2.0X103
m/s
=2.0X103
m/s
说明:n越大(即卫星越高),卫星的线速度越小。若n=0,即近地卫星,则卫星的线速度为V0=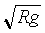 =7.9X103m/s,这就是第一宇宙速度,即环绕速度。
=7.9X103m/s,这就是第一宇宙速度,即环绕速度。
7、某人造地球卫星的高度是地球半径的15倍。试估算此卫星的线速度。已知地球半径R=6400km,g=10m/s2。
分析与解:人造地球卫星绕地球做圆周运动的向心力由地球对卫星的引力提供,设地球与卫星的质量分别为M、m,则: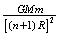 =
=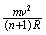 [1]
[1]
又根据近地卫星受到的引力可近似地认为等于其重力,即:mg=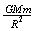 [2]
[2]
6、如图6-1所示,A、B两物体的质量分别是m1和m2,其接触面光滑,与水平面的夹角为θ,若A、B与水平地面的动摩擦系数都是μ,用水平力F推A,使A、B一起加速运动,求:(1)A、B间的相互作用力 (2)为维持A、B间不发生相对滑动,力F的取值范围。
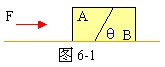
分析与解:A在F的作用下,有沿A、B间斜面向上运动的趋势,据题意,为维持A、B间不发生相对滑动时,A处刚脱离水平面,即A不受到水平面的支持力,此时A与水平面间的摩擦力为零。
本题在求A、B间相互作用力N和B受到的摩擦力f2时,运用隔离法;而求A、B组成的系统的加速度时,运用整体法。
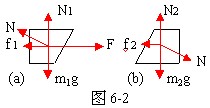
(1)对A受力分析如图6-2(a)所示,据题意有:N1=0,f1=0
因此有:Ncosθ=m1g [1] , F-Nsinθ=m1a [2]
由[1]式得A、B间相互作用力为:N=m1g/cosθ
(2)对B受力分析如图6-2(b)所示,则:N2=m2g+Ncosθ [3] , f2=μN2 [4]
将[1]、[3]代入[4]式得: f2=μ(m1+ m2)g
取A、B组成的系统,有:F-f2=(m1+ m2)a [5]
由[1]、[2]、[5]式解得:F=m1g(m1+ m2)(tgθ-μ)/m2
故A、B不发生相对滑动时F的取值范围为:0<F≤m1g(m1+ m2)(tgθ-μ)/m2
想一想:当A、B与水平地面间光滑时,且又m1=m2=m时,则F的取值范围是多少?(0<F≤2mgtgθ=。
5、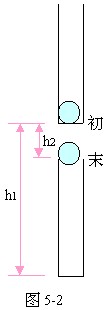 如图5-1所示,长L=75cm的静止直筒中有一不计大小的小球,筒与球的总质量为4千克,现对筒施加一竖直向下、大小为21牛的恒力,使筒竖直向下运动,经t=0.5秒时间,小球恰好跃出筒口。求:小球的质量。(取g=10m/s2)
如图5-1所示,长L=75cm的静止直筒中有一不计大小的小球,筒与球的总质量为4千克,现对筒施加一竖直向下、大小为21牛的恒力,使筒竖直向下运动,经t=0.5秒时间,小球恰好跃出筒口。求:小球的质量。(取g=10m/s2)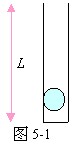
分析与解:筒受到竖直向下的力作用后做竖直向下的匀加速运动,且加速度大于重力加速度。而小球则是在筒内做自由落体运动。小球跃出筒口时,筒的位移比小球的位移多一个筒的长度。
设筒与小球的总质量为M,小球的质量为m,筒在重力及恒力的共同作用下竖直向下做初速为零的匀加速运动,设加速度为a;小球做自由落体运动。设在时间t内,筒与小球的位移分别为h1、h2(球可视为质点)如图5-2所示。
由运动学公式得:
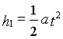
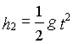
又有:L=h1-h2 代入数据解得:a=16米/秒2
又因为筒受到重力(M-m)g和向下作用力F,据牛顿第二定律:
F+(M-m)g=(M-m)a 得: 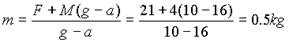
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com