
题目列表(包括答案和解析)
5.关于核力,下列说法中正确的是:( )
A.核力是一种特殊的万有引力
B.原子核由任意两个核子内部有核力作用
C.核力是原子核所稳定存在的原因
D.核力是一种短程强作用力
(知识点:核力。 能力培养:理解能力。)
4.图为查德威克实验示意图,由于天然放射性元素钋(Po)放出的α射线轰击铍时会产生粒子流A,用粒子流A轰击石石昔 时会打出粒子流B,经研究知道:( )
A.A为中子,B为质子。 B.A为质子,B为中子。
C.A为γ射线,B为中子。 D.A为中子,B为γ射线。
(知识点:考查原子核的人工转变(发现中子的过程)。能力培养:推理能力、实验能力。)
3.以下几个原子核反应中,X代表α粒子的反应式是:( )
A.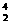 He+
He+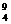 Be→
Be→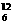 C+X B.
C+X B.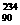 Th→
Th→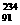 Pa+X
Pa+X
C.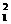 H+
H+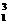 H→
H→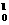 n+X D.
n+X D.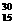 P→
P→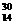 Si+X
Si+X
(知识点:考查原子核反应遵循的两个原则。 能力培养:理解能力。)
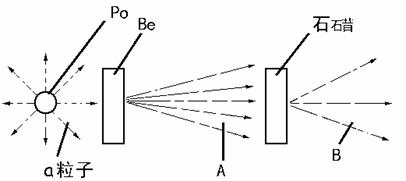
4题图
2.下列说法正确的是( )
A.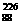 Ra衰变为
Ra衰变为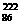 Rn要经过1次α衰变和1次β衰变。
Rn要经过1次α衰变和1次β衰变。
B.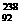 U衰变为
U衰变为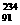 Pa要经过1次α衰变和1次β衰变。
Pa要经过1次α衰变和1次β衰变。
C.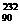 Th衰变为
Th衰变为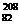 Pb要经过6次α衰变和4次β衰变。
Pb要经过6次α衰变和4次β衰变。
D.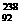 U衰变为
U衰变为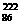 Rn要经过4次α衰变和4次β衰变。
Rn要经过4次α衰变和4次β衰变。
(知识点:衰变规律。能力培养:理解能力、推理能力、分析综合能力。)
1.天然放射现象的发现揭示了( )
A.原子不可再分 B.原子的核式结构
C.原子核还可再分 D.原子核由质子和中子组成
(知识点:考查天然放射现象。能力培养:理解能力。)
6.太阳现正处于主序星演化阶段.它主要是由正、负电子和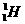 、
、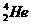 等原子核组成,维持太阳辐射的是它内部的核聚变反应,核反应方程是4
等原子核组成,维持太阳辐射的是它内部的核聚变反应,核反应方程是4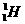
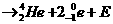 (释放的核能),这些核能最后转化为辐射能.根据目前关于恒星演化的理论,若由于聚变反应而使太阳中的
(释放的核能),这些核能最后转化为辐射能.根据目前关于恒星演化的理论,若由于聚变反应而使太阳中的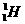 核数目从现有数减少10%,太阳将离开主序星阶段而转入红巨星的演化阶段,为了简化,假定目前太阳全部由
核数目从现有数减少10%,太阳将离开主序星阶段而转入红巨星的演化阶段,为了简化,假定目前太阳全部由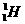 核组成.
核组成.
(1)为了研究太阳演化进程,需知道目前太阳的质量M,已知地球半径R=6.4×106 m,地球质量m=6.0×1024 kg,日地中心的距离r=1. 5×1011 m,地球表面处的重力加速度g=10 m/s2,1年约为3.2×107s,试估算目前太阳的质量M.
(2)已知质子质量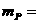 1. 672 6 X 10-27
kg,He质量
1. 672 6 X 10-27
kg,He质量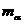 =6.645 8×10-27 kg,电子质量
=6.645 8×10-27 kg,电子质量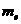 = 0. 9×10-30㎏,光速c=3×108
m/s,求每发生一次题中所述的核聚变反应所释放的核能.
= 0. 9×10-30㎏,光速c=3×108
m/s,求每发生一次题中所述的核聚变反应所释放的核能.
(3)已知地球上与太阳光垂直的每平方米截面上,每秒通过的太阳辐射能W=1. 35×103 W/m2.试估算太阳继续保持在主序星阶段还有多少年的寿命(估算结果只要求一位有效数).
解:(1)估算太阳的质量M,设T为地球绕日心运动的周期,则由万有引力定律和牛顿定律可知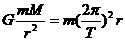 ,
,
地球表面重力加速度为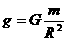 ,
,
联立解得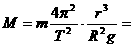 2×1030kg.
2×1030kg.
(2)根据质量亏损和质能公式,该核反应每发生一次释放的核能为
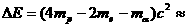 4×10-12 J.
4×10-12 J.
(3)根据题给假定,在太阳继续保持在主序星阶段的时间内,发生题中所述的核聚变反应的次数为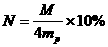 ,
,
因此,太阳总共辐射的能量为E=N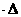 E.
E.
设太阳辐射是各向同性的,则每秒内太阳向外放出的辐射能力为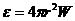 ,
,
所以太阳继续保持在主序星的时间为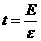 ,
,
由以上各式解得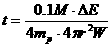 ,
,
以题给数据代入,并以年为单位,可得t≈l ×1010年=1百亿年.
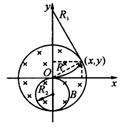
5.如图所示,在xOy平面上,一个以原点O为中心、半径为R的圆形区域内存在着一匀强磁场,磁场的磁感应强度为B,方向垂直于xOy平面向内.在O处原来静止着一个具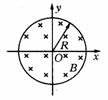 有放射性的原子核
有放射性的原子核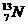 (氮),某时刻该核发生衰变,放出一个正电子和一个反冲核.已知正电子从O点射出时沿小x轴正方向,而反冲核刚好不会离开磁场区域,正电子电荷量为e.不计重力影响和粒子间的相互作用.
(氮),某时刻该核发生衰变,放出一个正电子和一个反冲核.已知正电子从O点射出时沿小x轴正方向,而反冲核刚好不会离开磁场区域,正电子电荷量为e.不计重力影响和粒子间的相互作用.
(1)试写出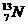 的衰变方程;
的衰变方程;
(2)求正电子离开磁场区域时的位置.
解:(1) 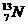
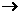
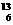 C+
C+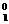 e.
e.
(2)设正电子质量为m1,速度为v1,轨道半径为R1,反冲核质量为m2,速度为v2 ,轨道半径为R2.如图所示,正电子电荷量为e,反冲核电荷量q=6e.据动量守恒定律,有m1v1= m2 v2,
 正电子的轨道半径
正电子的轨道半径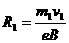 ,反冲核的轨道半径
,反冲核的轨道半径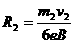 ,据题意知
,据题意知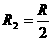 ,由以上各式得R1=3R,设正电子离开磁场区域的位置坐标为(x,y),由几何关系得
,由以上各式得R1=3R,设正电子离开磁场区域的位置坐标为(x,y),由几何关系得
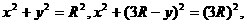
解得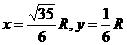
4.1930年科学家发现钋放出的射线贯穿能力极强,它甚至能穿透几厘米厚的铅板,1932年,英国年轻物理学家查德威克用这种未知射线分别轰击氢原子和氮原子,结果打出一些氢核和氮核.若未知射线均与静止的氢核和氮核正碰,测出被打出的氢核最大速度为vH=3.5×107m/s,被打出的氮核的最大速度vN=4. 7×106
m/s,假定正碰时无机械能损失,设未知射线中粒子质量为m,初速为v,质子的质量为 .
.
(1)推导被打出的氢核和氮核的速度表达式;
(2)根据上述数据,推算出未知射线中粒子的质量m与质子的质量 之比(已知氮核质量为氢核质量的14倍).
之比(已知氮核质量为氢核质量的14倍).
解:(1)碰撞满足动量守恒和机械能守恒,与氢核碰撞时有
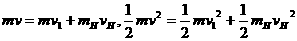
解之得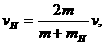 同理可得
同理可得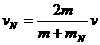 .
.
(2)由上面可得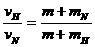 ,代入数据得
,代入数据得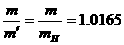
3.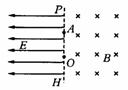 如图所示,在某一足够大的真空室中,虚线PH的右侧是一磁感应强度为B、方向垂直纸面向里的匀强磁场,左侧是一场强为E、方向水平向左的匀强电场.在虚线PH上的点O处有一质量为M、电荷量为Q的镭核(
如图所示,在某一足够大的真空室中,虚线PH的右侧是一磁感应强度为B、方向垂直纸面向里的匀强磁场,左侧是一场强为E、方向水平向左的匀强电场.在虚线PH上的点O处有一质量为M、电荷量为Q的镭核(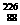 Ra).某时刻原来静止的镭核水平向右放出一个质量为m、电荷量为q的
Ra).某时刻原来静止的镭核水平向右放出一个质量为m、电荷量为q的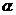 粒子而衰变为氡(Rn)核,设
粒子而衰变为氡(Rn)核,设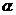 粒子与氡核分离后它们之间的作用力忽略不计,涉及动量问题时,亏损的质量可不计.
粒子与氡核分离后它们之间的作用力忽略不计,涉及动量问题时,亏损的质量可不计.
(1)写出镭核衰变为氡核的核反应方程;
(2)经过一段时间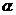 粒子刚好到达虚线PH上的A点,测得
粒子刚好到达虚线PH上的A点,测得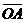 = L.求此时刻氡核的速率.
= L.求此时刻氡核的速率.
解:(1) 核反应方程为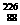 Ra
Ra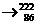 Rn+
Rn+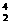 He.
He.
(2)设衰变后,氡核的速度为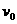 ,
,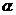 粒子速度为
粒子速度为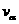 ,由动量守恒定律得
,由动量守恒定律得
(M一m) 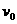 =m
=m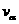 ,
,
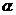 粒子在匀强磁场中做匀速圆周运动,到达A点需要的时间为
粒子在匀强磁场中做匀速圆周运动,到达A点需要的时间为
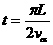 ,又
,又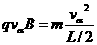
氡核在电场中做匀加速直线运动,t时刻速度为v=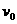 +at,
+at,
氡核的加速度为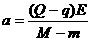 ,
,
由以上各式解得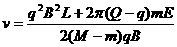
2.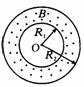 据有关资料介绍,受控热核聚变反应装置中有极高的温度,因而带电粒子将没有通常意义上的容器可装,而是由磁场约束带电粒子运动将其束缚在某个区域内,现按下面的简化条件来讨论这个问题,如图所示,有一个环形区域,其截面内半径为
据有关资料介绍,受控热核聚变反应装置中有极高的温度,因而带电粒子将没有通常意义上的容器可装,而是由磁场约束带电粒子运动将其束缚在某个区域内,现按下面的简化条件来讨论这个问题,如图所示,有一个环形区域,其截面内半径为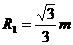 ,外半径为R2=1.
0 m,区域内有垂直纸面向里的匀强磁场,已知磁感应强度B=1.0 T,被束缚粒子的荷质比为
,外半径为R2=1.
0 m,区域内有垂直纸面向里的匀强磁场,已知磁感应强度B=1.0 T,被束缚粒子的荷质比为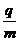 =4.0×107C/kg,不计带电粒子在运动过程中的相互作用,不计带电粒子的重力.
=4.0×107C/kg,不计带电粒子在运动过程中的相互作用,不计带电粒子的重力.
(1)若中空区域中的带电粒子沿环的半径方向射入磁场,求带电粒子不能穿越磁场外边界的最大速度v0.
(2)若中空区域中的带电粒子以(1)中的最大速度v0沿圆环半径方向射入磁场,求带电粒子从进入磁场开始到第一次回到该点所需要的时间t.
解:设粒子在磁场中做圆周运动的最大半径为r,则r=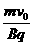 ,如图所示,由几何关系得
,如图所示,由几何关系得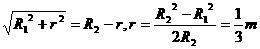
则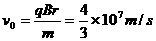 .
.
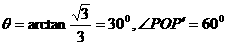 。
。
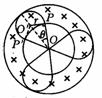 故带电粒子进入磁场绕圆
故带电粒子进入磁场绕圆 转过3600 -(1800一600)=2400又回到中空部分.粒子的运动轨迹如图所示,故粒子从P点进入磁场到第一次回到P点时,粒子在磁场中运动时间为
转过3600 -(1800一600)=2400又回到中空部分.粒子的运动轨迹如图所示,故粒子从P点进入磁场到第一次回到P点时,粒子在磁场中运动时间为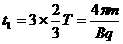 ,
,
粒子在中空部分运动时间为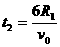 ,
,
粒子运动的总时间为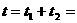
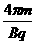 +
+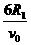 =5.74×10-7s.
=5.74×10-7s.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com