
题目列表(包括答案和解析)
25、(2005年台州)如图,用长为18 m的篱笆(虚线部分),两面靠墙围成矩形的苗圃.
(1)设矩形的一边为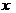 (m),面积为
(m),面积为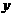 (m2),求
(m2),求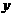 关于
关于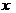 的函数关系式,并写出自变量
的函数关系式,并写出自变量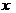 的取值范围;
的取值范围;
(2)当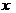 为何值时,所围苗圃的面积最大,最大面积是多少?
为何值时,所围苗圃的面积最大,最大面积是多少?
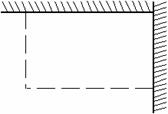
解:(1) 由已知,矩形的另一边长为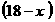

则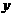 =
= 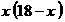
=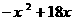
自变量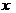 的取值范围是0<
的取值范围是0<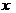 <18.
<18.
(2)∵
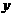 =
=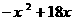 =
=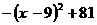
∴ 当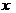 =9时(0<9<18),苗圃的面积最大
=9时(0<9<18),苗圃的面积最大
最大面积是81 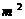
又解: ∵  =-1<0,
=-1<0,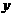 有最大值,
有最大值,
∴ 当 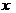 =
=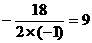 时(0<9<18),
时(0<9<18),
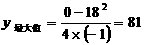 (
(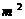 )
)
24、26(2005年惠安县)如图,抛物线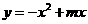 过点A(4,0),O为坐标原点,
过点A(4,0),O为坐标原点,
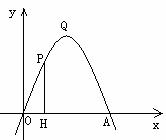 Q是抛物线的顶点. ⑴求
Q是抛物线的顶点. ⑴求 的值;⑵点P是
的值;⑵点P是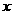 轴上方抛物线上的一个动点,过P作PH⊥
轴上方抛物线上的一个动点,过P作PH⊥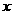 轴,H为垂足.有一个同学说:“在
轴,H为垂足.有一个同学说:“在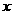 轴上方抛物线上的所有点中,抛物线的顶点Q与
轴上方抛物线上的所有点中,抛物线的顶点Q与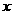 轴相距最远,所以当点P运动至点Q时,折线P-H-O的长度最长”,请你用所学知识判断:这个同学的说法是否正确.
轴相距最远,所以当点P运动至点Q时,折线P-H-O的长度最长”,请你用所学知识判断:这个同学的说法是否正确.
解:⑴∵点A(4,0)在抛物线上 ∴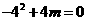 ∴
∴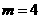 ∴
∴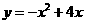
 ⑵设点P的坐标为
⑵设点P的坐标为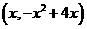
 ∴
∴ 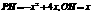
∴折线P-H-O的长度

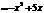

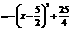 ∴当
∴当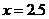 时,折线P-H-O的长度最长为
时,折线P-H-O的长度最长为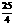 ∵点Q的横坐标为2∴这个同学的说法不正确。
∵点Q的横坐标为2∴这个同学的说法不正确。
23、(2005年漳州)如图,已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与x轴交于A、B两点(点A在点B左侧),与y轴交于点C。
(1)求抛物线的解析式及点A、B、C的坐标;
(2)若直线y=kx+t经过C、M两点,且与x轴交于点D,试证明四边形CDAN是平行四边形;
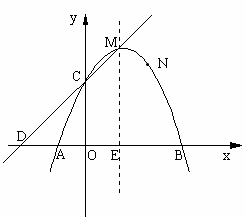 (3)点P在抛物线的对称轴x=1上运动,请探索:在x轴上方是否存在这样的P点,使以P为圆心的圆经过A、B两点,并且与直线CD相切,若存在,请求出点P的坐标;若不存在,请说明理由。
(3)点P在抛物线的对称轴x=1上运动,请探索:在x轴上方是否存在这样的P点,使以P为圆心的圆经过A、B两点,并且与直线CD相切,若存在,请求出点P的坐标;若不存在,请说明理由。
解:(1)由抛物线的顶点是M(1,4),设解析式为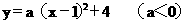
又抛物线经过点N(2,3),所以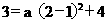 解得a=-1
解得a=-1
所以所求抛物线的解析式为y=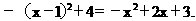
令y=0,得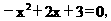 解得:
解得: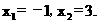
得A(-1,0) B(3,0) ;
令x=0,得y=3,所以 C(0,3).
(2)直线y=kx+t经过C、M两点,所以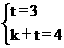 即k=1,t=3
即k=1,t=3
直线解析式为y=x+3.
令y=0,得x=-3,故D(-3,0) CD=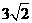
连接AN,过N做x轴的垂线,垂足为F.
设过A、N两点的直线的解析式为y=mx+n,
则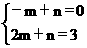 解得m=1,n=1
解得m=1,n=1
所以过A、N两点的直线的解析式为y=x+1
所以DC∥AN.
在Rt△ANF中,AN=3,NF=3,所以AN=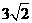
所以DC=AN。
因此四边形CDAN是平行四边形.
(3)假设在x轴上方存在这样的P点,使以P为圆心的圆经过A、B两点,并且与直线CD相切,设P(1,u) 其中u>0,则PA是圆的半径且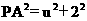
过P做直线CD的垂线,垂足为Q,则PQ=PA时以P为圆心的圆与直线CD相切。
由第(2)小题易得:△MDE为等腰直角三角形,故△PQM也是等腰直角三角形,
由P(1,u)得PE=u, PM=|4-u|, PQ=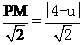
由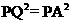 得方程:
得方程: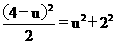 ,解得
,解得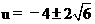 ,
,
舍去负值u=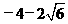 ,符合题意的u=
,符合题意的u=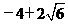 ,
,
所以,满足题意的点P存在,其坐标为(1,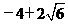 ).
).
22、(2005年海安县)如图,已知抛物线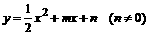 与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.
与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.
(1)求抛物线的解析式。
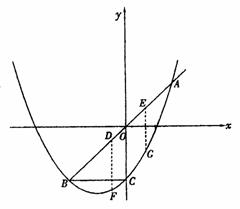 (2)设D、E是线段AB上异于A、B的两个动点(点E在点D的上方),DE=
(2)设D、E是线段AB上异于A、B的两个动点(点E在点D的上方),DE=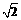 ,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
(1)∵抛物线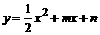 与y轴交于点C
∴C(0,n)
与y轴交于点C
∴C(0,n)
∵BC∥x轴 ∴B点的纵坐标为n
∵B、A在y=x上,且OA=OB ∴B(n,n),A(-n,-n)
∴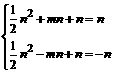 解得:n=0(舍去),n=-2;m=1
解得:n=0(舍去),n=-2;m=1
∴所求解析式为: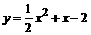
(2)作DH⊥EG于H
∵D、E在直线y=x上 ∴∠EDH=45° ∴DH=EH
∵DE=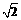 ∴DH=EH=1
∵D(x,x) ∴E(x+1,x+1)
∴DH=EH=1
∵D(x,x) ∴E(x+1,x+1)
∴F的纵坐标: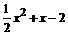 ,G的纵坐标:
,G的纵坐标: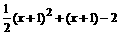
∴DF=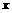 -(
-(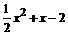 )=2-
)=2-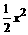 EG=(x+1)- [
EG=(x+1)- [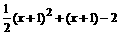 ]=2-
]=2-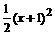
∴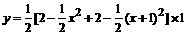
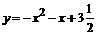
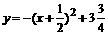
∴x的取值范围是-2<x<1 当x=-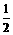 时,y最大值=3
时,y最大值=3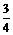 .
.
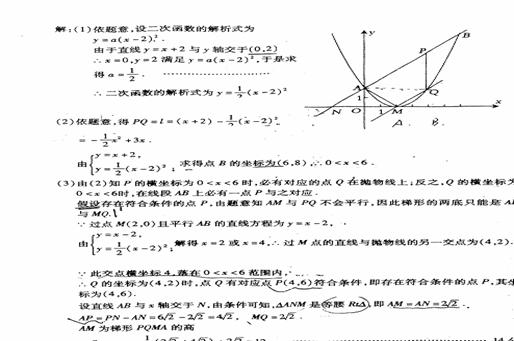
21、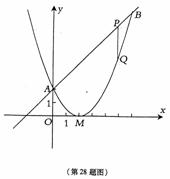 (2005年龙岩市)已知二次函数图象的顶点坐标为M(2,0),直线y=x+2与该二次函数的图象交于A、B两点,其中点A在y轴上(如图示) (1)求该二次函数的解析式; (2)P为线段用上一动点(A、B两端点除外),过P作x轴的垂线与二次函数的图象交于点Q,设线段PQ的长为
(2005年龙岩市)已知二次函数图象的顶点坐标为M(2,0),直线y=x+2与该二次函数的图象交于A、B两点,其中点A在y轴上(如图示) (1)求该二次函数的解析式; (2)P为线段用上一动点(A、B两端点除外),过P作x轴的垂线与二次函数的图象交于点Q,设线段PQ的长为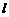 ,点P的横坐标为x,求出
,点P的横坐标为x,求出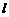 与x之间的函数关系式,并求出自变量x的取值范围;(3)在(2)的条件下,线段AB上是否P,使四边形PQMA为梯形.若存在,求出
与x之间的函数关系式,并求出自变量x的取值范围;(3)在(2)的条件下,线段AB上是否P,使四边形PQMA为梯形.若存在,求出
点P的坐标,并求出梯形的面积;若不存在,请说明理由.
20、(2005年梅州市)东海体育用品商场为了推销某一运动服,先做了市场调查,得到数据如下表:
|
卖出价格x(元/件) |
50 |
51 |
52 |
53 |
 …… …… |
|
销售量p(件) |
500 |
490 |
480 |
470 |
…… |
(1)以x作为点的横坐标,p作为纵坐标,把表中的
数据,在图8中的直角坐标系中描出相应的点,观察连结
各点所得的图形,判断p与x的函数关系式;
(2)如果这种运动服的买入件为每件40元,试求销售
利润y(元)与卖出价格x(元/件)的函数关系式
(销售利润=销售收入-买入支出);
(3)在(2)的条件下,当卖出价为多少时,能获得最大利润?
解:(1)p与x成一次函数关系。
设函数关系式为p=kx+b ,则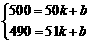
解得:k=-10,b=1000 , ∴ p=-10x+1000
经检验可知:当x=52,p=480,当x=53,p=470时也适合这一关系式
∴所求的函数关系为p=-10x+1000
(2)依题意得:y=px-40p=(-10x+1000)x-40(-10x+1000)
∴ y=-10x2+1400x-40000
(3)由y=-10x2+1400x-40000 可知,当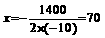 时,y有最大值
时,y有最大值
∴ 卖出价格为70元时,能花得最大利润。
19、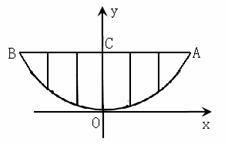 (丽水市2005)某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.
(丽水市2005)某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.
(1) 以O为原点,OC所在的直线为y轴建立平面直角坐标系,请根据以上的数据,求出抛物线y=ax2的解析式;
(2)计算一段栅栏所需立柱的总长度.(精确到0.1米)
解:(1) 由已知:OC=0.6,AC=0.6, 得点A的坐标为(0.6,0.6),
代入y=ax2,得a=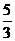 , ∴抛物线的解析式为y=
, ∴抛物线的解析式为y=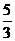 x2.
x2.
(2)点D1,D2的横坐标分别为0.2,0.4, 代入y=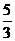 x2,得点D1,D2的纵坐标分别为: y1=
x2,得点D1,D2的纵坐标分别为: y1=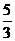 ×0.22≈0.07,y2=
×0.22≈0.07,y2=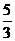 ×0.42≈0.27, ∴立柱C1D1=0.6-0.07=0.53,C2D2=0.6-0.27=0.33,
由于抛物线关于y轴对称,栅栏所需立柱的总长度为: 2(C1D1+ C2D2)+OC=2(0.53+0.33)+0.6≈2.3米.
×0.42≈0.27, ∴立柱C1D1=0.6-0.07=0.53,C2D2=0.6-0.27=0.33,
由于抛物线关于y轴对称,栅栏所需立柱的总长度为: 2(C1D1+ C2D2)+OC=2(0.53+0.33)+0.6≈2.3米.
18、(2005马尾区)已知抛物线y=x2+(2n-1)x+n2-1 (n为常数).
(1)当该抛物线经过坐标原点,并且顶点在第四象限时,求出它所对应的函数关系式;
(2)设A是(1)所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点,过A作x轴的平行线,交抛物线于另一点D,再作AB⊥x轴于B,DC⊥x轴于C.
①当BC=1时,求矩形ABCD的周长;
②试问矩形ABCD的周长是否存在最大值?如果存在,请求出这个最大值,并指出此时A点的坐标;如果不存在,请说明理由.
解:(1)由已知条件,得:n2-1=0
解这个方程,得: n1=1 ,n2=-1;
当n=1时,得y=x2+x,此抛物线的顶点不在第四象限;
当n=-1时,得y=x2-3x,此抛物线的顶点在第四象限;
∴所求的函数关系式为y=x2-3x
(2)由y=x2-3x,令y=0,得x2-3x=0,解得x1=0 ,x2=3;
∴抛物线与x 轴的另一个交点为(3,0)
∴它的顶点为(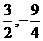 ),对称轴为直线x=
),对称轴为直线x=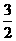
①∵BC=1,由抛物线和矩形的对称性易知OB=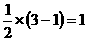
∴B(1,0)
∴点A的横坐标x=1,又点A在抛物线y=x2-3x上,
∴点A的纵坐标y=12-3×1=-2。
∴AB=|y |=2
∴矩形ABCD的周长为:2(AB+BC)=6
②∵点A在抛物线y=x2-3x上,可以设A点的坐标为(x,x2-3x),
∴B点的坐标为 (x,0)。(0<x<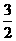
∴BC=3-2x,A在x 轴的下方,
∴x2-3x<0
∴AB=| x2-3x |=3x-x2
∴矩形ABCD的周长P=2((3x-x2)+(3-2x))=-2(x-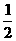 )2+
)2+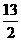
∵a=-2<0
∴当x=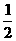 时, 矩形ABCD的周长P最大值是
时, 矩形ABCD的周长P最大值是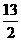 。
。
17、(2005马尾区)某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克. 经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6000元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
(1)设每千克应涨价x元,则(10+x)(500-20x)=6000 解得x=5或x=10,为了使顾客得到实惠,所以x=5.(2)设涨价x元时总利润为y, 则y=(10+x)(500-20x)= -20x2+300x+5000=-20(x-7.5) 2+6125 当x=7.5时,y取得最大值,最大值为6125.
15、 (兰州市2005)一条抛物线的对称轴是x=1且与x轴有惟一的公共点,并且开口方向向下,则这条抛物线的解析式是_y=-x2+2x-1__(任写一个) 16、(兰州市2005)已知二次函数y=ax2-4a图像的顶点坐标为(0,4)矩形ABCD在抛物线与x轴围成的图形内,顶点B、C在x轴上,顶点A、D在抛物线上,且A在D点的右侧, (1)求二次函数的解析式 (2)设点A的坐标为(x?y)试求矩形ABCD的周长L与自变量x的函数关系 (3)周长为10的矩形ABCD是否存在?若存在,请求出顶点A的坐标;若不存在,请说明理由。
解:(1)由题意得-4a=4 ∴a=-1∴二次函数的解析式为y=-x2+4 ?⑵?设点A(x?y)∵点A在抛物线y=-x2+4上∴y=-x2+4则AD=2x,AB=-x2+4 ∴L=2(AD+AB)=2(2x-x2+4)=-2x2+4x+8?0<x<2??⑶?当L=10时 -2x2+4x+8=10x2-2x+1=0 x1=x2=1∴当x=1时,y=-12+4=3∴存在周长为10的矩形ABCD,且点A的坐标为(1,3)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com