
题目列表(包括答案和解析)
4、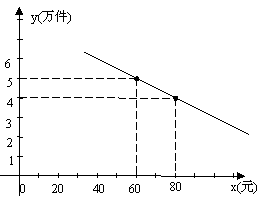 (长沙市 2005)某通讯器材公司销售一种市场需求较大的新型通讯产品.已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120 万元.在销售过程中发现,年销售量y(万件)与销售单价x(元)之问存在着如图所示的一次函数关系.
⑴求y关于x的函数关系式;
⑵试写出该公司销售该种产品的年获利z(万元)关于销售单价x(元)的函数关系式(年获利=年销售额一年销售产品总进价一年总开支).当销售单价x为何值时,年获利最大?并求这个最大值;
⑶若公司希望该种产品一年的销售获利不低于40万元,借助⑵中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
(长沙市 2005)某通讯器材公司销售一种市场需求较大的新型通讯产品.已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120 万元.在销售过程中发现,年销售量y(万件)与销售单价x(元)之问存在着如图所示的一次函数关系.
⑴求y关于x的函数关系式;
⑵试写出该公司销售该种产品的年获利z(万元)关于销售单价x(元)的函数关系式(年获利=年销售额一年销售产品总进价一年总开支).当销售单价x为何值时,年获利最大?并求这个最大值;
⑶若公司希望该种产品一年的销售获利不低于40万元,借助⑵中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
解:⑴设 ,它过点(60,5),(80,4)
,它过点(60,5),(80,4)
∴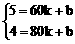 解得
解得 ∴
∴ ⑵
⑵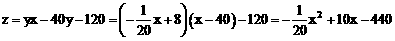
∴当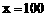 元时,最大年获得为60万元.…(6分)
元时,最大年获得为60万元.…(6分)
⑶令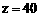 ,得
,得 ,整理得:
,整理得:  解得:
解得: ,
,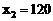 由图象可知,要使年获利不低于40万元,销售单价应在80元到120元之间.又因为销售单价越低,销售量越大所以要使销售量最大,又要使年获利不低于40万元,销售单价应定为80元.
由图象可知,要使年获利不低于40万元,销售单价应在80元到120元之间.又因为销售单价越低,销售量越大所以要使销售量最大,又要使年获利不低于40万元,销售单价应定为80元.
3、(长沙市 2005)已知抛物线 经过点A(
经过点A(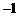 ,0)、B(m,0)(m>0),且与y轴交于点C.
⑴求a、b的值(用含m的式子表示);
⑵如图所示,⊙M过A、B、C三点,求阴影部分扇形的面积S(用含m的式子表示);⑶在x轴上方,若抛物线上存在点P,使得以A、B、P为顶点的三角形与
,0)、B(m,0)(m>0),且与y轴交于点C.
⑴求a、b的值(用含m的式子表示);
⑵如图所示,⊙M过A、B、C三点,求阴影部分扇形的面积S(用含m的式子表示);⑶在x轴上方,若抛物线上存在点P,使得以A、B、P为顶点的三角形与 相似,求m的值.
相似,求m的值.

⑴依题意得有 ,解得
,解得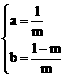
∴抛物线的解析式为: ⑵∵
⑵∵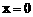 时,
时, ,∴C(0,
,∴C(0,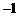 )
∵
)
∵ ,∴
,∴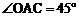 ,∴
,∴
又∵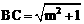 ,∴
,∴
⑶如图,由抛物线的对称性可知,若抛物线上存在点P, 使得以A、B、P为顶点的三角形与△ABC相似,则P关于对称轴的对称点P’也符合题惫,即P、P’对应的m值相同.下面以点P在对称轴右侧进行分析:
情形一:如图,ΔABC∽△APB
则 ,
,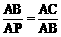 过点P作
过点P作 垂足为D,连PA、PB.在Rt△PDA中,∵
垂足为D,连PA、PB.在Rt△PDA中,∵ ,∴PD=AD,∴可令P(x,x+1)
,∴PD=AD,∴可令P(x,x+1)
若点P在抛物线上,
则有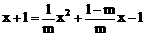
即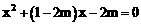 ,解得
,解得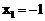 ,
, ∴
∴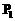 (2m,2m+1),
(2m,2m+1),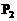 (-1,0).显然
(-1,0).显然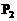 不合题意舍去.
不合题意舍去.
此时
又由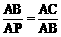 ,得
,得
由①、②有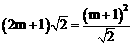
整理得: ,解得:
,解得: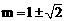 .
.
2、(2005年北京)已知:在平面直角坐标系xOy中,一次函数 的图象与x轴交于点A,抛物线
的图象与x轴交于点A,抛物线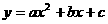 经过O、A两点。
经过O、A两点。
(1)试用含a的代数式表示b;
(2)设抛物线的顶点为D,以D为圆心,DA为半径的圆被x轴分为劣弧和优弧两部分。若将劣弧沿x轴翻折,翻折后的劣弧落在⊙D内,它所在的圆恰与OD相切,求⊙D半径的长及抛物线的解析式;
(3)设点B是满足(2)中条件的优弧上的一个动点,抛物线在x轴上方的部分上是否存在这样的点P,使得 ?若存在,求出点P的坐标;若不存在,请说明理由。
?若存在,求出点P的坐标;若不存在,请说明理由。
(1)解法一:∵一次函数 的图象与x轴交于点A
的图象与x轴交于点A
∴点A的坐标为(4,0) ∵抛物线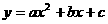 经过O、A两点
经过O、A两点


解法二:∵一次函数 的图象与x轴交于点A
的图象与x轴交于点A
∴点A的坐标为(4,0)
∵抛物线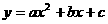 经过O、A两点
经过O、A两点
∴抛物线的对称轴为直线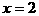

 (2)解:由抛物线的对称性可知,DO=DA ∴点O在⊙D上,且∠DOA=∠DAO 又由(1)知抛物线的解析式为
(2)解:由抛物线的对称性可知,DO=DA ∴点O在⊙D上,且∠DOA=∠DAO 又由(1)知抛物线的解析式为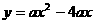 ∴点D的坐标为(
∴点D的坐标为(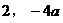 )
)
①当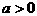 时,
时,

如图1,设⊙D被x轴分得的劣弧为 ,它沿x轴翻折后所得劣弧为
,它沿x轴翻折后所得劣弧为 ,显然
,显然 所在的圆与⊙D关于x轴对称,设它的圆心为D' ∴点D'与点D也关于x轴对称 ∵点O在⊙D'上,且⊙D与⊙D'相切 ∴点O为切点 ∴D'O⊥OD ∴∠DOA=∠D'OA=45° ∴△ADO为等腰直角三角形
所在的圆与⊙D关于x轴对称,设它的圆心为D' ∴点D'与点D也关于x轴对称 ∵点O在⊙D'上,且⊙D与⊙D'相切 ∴点O为切点 ∴D'O⊥OD ∴∠DOA=∠D'OA=45° ∴△ADO为等腰直角三角形
 ∴点D的纵坐标为
∴点D的纵坐标为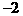
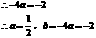
∴抛物线的解析式为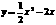 ②当
②当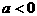 时, 同理可得:
时, 同理可得:
抛物线的解析式为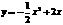 综上,⊙D半径的长为
综上,⊙D半径的长为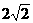 ,抛物线的解析式为
,抛物线的解析式为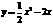 或
或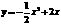
(3)解答:抛物线在x轴上方的部分上存在点P,使得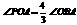
设点P的坐标为(x,y),且y>0
①当点P在抛物线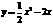 上时(如图2)
上时(如图2)

∵点B是⊙D的优弧上的一点 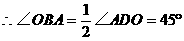
 过点P作PE⊥x轴于点E
过点P作PE⊥x轴于点E 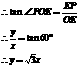
由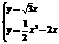 解得:
解得: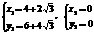 (舍去)
(舍去)
∴点P的坐标为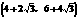
②当点P在抛物线 上时(如图3)
上时(如图3)

同理可得,
由 解得:
解得: (舍去) ∴点P的坐标为
(舍去) ∴点P的坐标为
综上,存在满足条件的点P,点P的坐标为 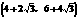 或
或
1、(2005年安徽)一列火车自A城驶往B城,沿途有n 个车站(包括起点站A和终点站B),该列火车挂有一节邮政车厢,运行时需要在每个车站停靠,每停靠一站不仅要卸下已经通过的各车站发给该站的邮包一个,还要装上该站发往下面行程中每个车站的邮包一个.
例如,当列车停靠在第x 个车站时,邮政车厢上需要卸下已经通过的(x-1)个车站发给该站的邮包共(x-1)个,还要装上下面行程中要停靠的(n-x)个车站的邮包共(n-x)个.
(1)根据题意,完成下表:
|
车站序号 |
在第x车站启程时邮政车厢邮包总数 |
|
1 |
n-1 |
|
2 |
(n-1)-1+(n-2)=2(n-2) |
|
3 |
2(n-2)-2+(n-3)=3(n-3) |
|
4 |
|
|
5 |
|
|
… |
…… |
|
n |
|
(2)根据上表,写出列车在第x车站启程时,邮政车厢上共有邮包的个数y(用x、n表示).
(3)当n=18时,列车在第几个车站启程时邮政车厢上邮包的个数最多?
(1)
|
车站序号 |
在第x车站启程时邮政车厢邮包总数 |
|
1 |
n-1 |
|
2 |
(n-1)-1+(n-2)=2(n-2) |
|
3 |
2(n-2)-2+(n-3)=3(n-3) |
|
4 |
3(n-3)-3+(n-4)=4(n-4) |
|
5 |
4(n-4)-4+(n-5)=5(n-5) |
|
… |
…… |
|
n |
0 |
(2)y=x(n-x);(3)当n=18时,y=x(18-x)=-x2+18x=-(x-9)2+81,当x=9时,y 取得最大值.所以列车在第9个车站启程时,邮政车厢上邮包的个数最多.
26、
25、(福州2005)如图2射线OC的端点O在直线AB上,∠AOC的度数比∠BOC的2倍多10°。设∠AOC和∠BOC的度数分别为x、y,则下列正确的方程组为…………( B )
 A、
A、 B、
B、
C、 D、
D、
24、(河南2004)若 与
与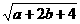 互为相反数,则
互为相反数,则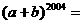 __
__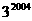 _____。
_____。
23、(安徽2004)某电视台在黄金时段的2分钟广告时间内,计划插播长度为15秒和30秒的两种广告。15秒广告每播1次收费0.6万元,30秒广告每播1次收费1万元。若要求每种广告播放不少于2次。问:
(1)两广告的播放的次数有几种安排方式?
(2)电视台选择哪种方式播放收益较大?
(1)设15秒广告播放x次,30秒广告播放y次,由题意得
15x+30y=120,
解得x=4,y=2或x=2,y=3。
(2)若x=4,y=2时,0.6×4+1×2=4.4万元;
若x=2,y=3时,0.6×2+1×3=4.2万元。
故播放15秒广告4次,30秒广告2次的方式,收益较大。
22、(绍兴市2004)初三(2)班的一个综合实践活动小组去A,B两个超市调查去年和今年“五一节”期间的销售情况,下图是调查后小敏与其他两位同学交流的情况.根据他们的对话,请你分别求出A,B两个超市今年“五一节” 期间的销售额.



设去年A超市销售额为x万元,B 超市销售额为y万元,
由题意得
解得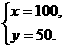
100(1+15%)=115(万元),50(1+10%)=55(万元).
21、(2004年苏州)西部山区某县响应国家“退耕还林”号召,将该县一部分耕地改还林地。改还后,林地面积和耕地面积共有180km2, 耕地面积是林地面积的25%。设改还后耕地面积为x km2 ,林地面积为ykm2,则下列方程组中,正确的是 ( A )

 A
x+y=180
B.
x+y=180
A
x+y=180
B.
x+y=180
x=25%y y=25%x

 C.
x+y=180
D. x+y=180
C.
x+y=180
D. x+y=180
x-y=25% y-x=25%
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com