
题目列表(包括答案和解析)
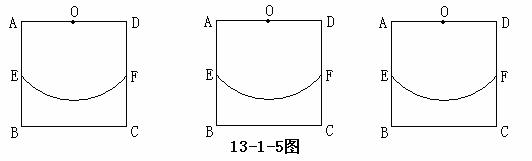
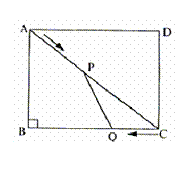
5、如图,在边长为2个单位长度的正方形ABCD中,点O、E分别是AD、AB的中点,点F是以点O为圆心、OE的长为半径的圆弧与DC的交点,点P是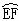 上的动点,连结OP,并延长交直线BC于点
上的动点,连结OP,并延长交直线BC于点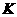 .
.
(1)当点P从点E沿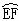 运动到点F时,点
运动到点F时,点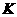 运动了多少个单位长度?
运动了多少个单位长度?
(2)过点P作 所在圆的切线,当该切线不与BC平行时,设它与射线AB、直线BC分别
所在圆的切线,当该切线不与BC平行时,设它与射线AB、直线BC分别
交于点M、G.
①当K与B重合时,BG∶BM的值是多少?
②在点P运动的过程中,是否存在BG∶BM=3的情况?你若认为存在,请求出BK的值;你若认为不存在,试说明其中的理由.
一般地,是否存在BG∶BM=n(n为正整数)的情况?试提出你的猜想(不要求证明).
 例2如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB向点B移动,设P、Q两点移动t秒(0<t<5)后,四边形ABQP的面积为S米2。
例2如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB向点B移动,设P、Q两点移动t秒(0<t<5)后,四边形ABQP的面积为S米2。
(1)求面积S与时间t的关系式;
(2)在P、Q两点移动的过程中,四边形ABQP与△CPQ的面积能否相等?若能,求出此时点P的位置;若不能,请说明理由。
分析:本题是一个动态几何问题,也是一个数形结合的典型问题,综合性较强。
解:(1)过点P作(1) 设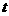 秒后,
秒后, 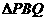 的面积是
的面积是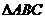 的面积的一半,
的面积的一半,
则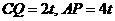 , 根据题意, 列出方程
, 根据题意, 列出方程
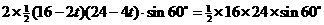 ,
,
化简, 得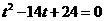 ,
,
解得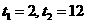 . 所以2秒和12秒均符合题意;
. 所以2秒和12秒均符合题意;
(2) 当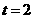 时,
时, 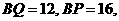 在
在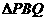 中, 作
中, 作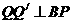 于
于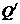 ,
,
在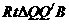 和
和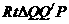 中,
中, 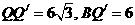 ,
,
所以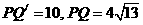 ;
;
当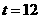 时,
时, 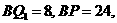 同理可求得
同理可求得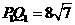 .
.
说明:本题考查的知识点较多,考查了勾股定理、平行线分线段成比例定理,一元二次方程及一元二次方程及根的判别式。
练习二
4、如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21。动点P从点D出发,沿射线DA的方向以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动。设运动的时间为t(秒)。
(1)设△BPQ的面积为S,求S与t之间的函数关系式;
(2)当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?
(3)当线段PQ与线段AB相交于点O,且2AO=OB时,求∠BQP的正切值;
(4)是否存在时刻t,使得PQ⊥BD?若存在,求出t的值;若不存在,请说明理由。
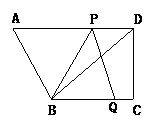
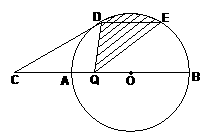
3、如图,AB是⊙O的直径,点C是BA延长线上一点,CD切⊙O于D点,弦DE∥CB,Q是AB上一动点,CA=1,CD是⊙O半径的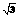 倍。
倍。
(1)求⊙O的半径R。
(2)当Q从A向B运动的过程中,图中阴影部分的面积是否发生变化,若发生变化,请你说明理由;若不发生变化,请你求出阴影部分的面积。
2、已知,如图(甲),正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点, P不运动到M和C,以AB为直径做⊙O,过点P作⊙O的切线交AD于点F,切点为E.
(1)求四边形CDFP的周长;
(2)试探索P在线段MC上运动时,求AF·BP的值;
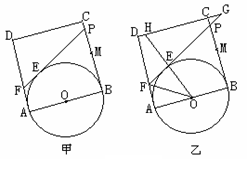 (3)延长DC、FP相交于点G,连结OE并延长交直线DC于H(如图乙),是否存在点P,
(3)延长DC、FP相交于点G,连结OE并延长交直线DC于H(如图乙),是否存在点P,
使△EFO∽△EHG?如果存在,试求此时的BP的长;如果不存在,请说明理由。
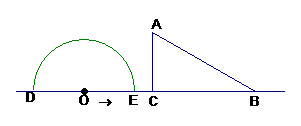
1、如图,形如量角器的半圆O的直径DE=12cm,形如三角板的⊿ABC中,∠ACB=90°,∠ABC=30°,BC=12cm。半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上。设运动时间为t (s),当t=0s时,半圆O在⊿ABC的左侧,OC=8cm。
(1)当t为何值时,⊿ABC的一边所在直线与半圆O所在的圆相切?
(2)当⊿ABC的一边所在直线与半圆O所在的圆相切时,如果半圆O与直线DE围成的区域与⊿ABC三边围成的区域有重叠部分,求重叠部分的面积。
15.(12分) 反比例函数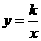 和一次函数y=mx+n的图象的一个交点A(-3,4),且一次函数的图像与x轴的交点到原点的距离为5.
和一次函数y=mx+n的图象的一个交点A(-3,4),且一次函数的图像与x轴的交点到原点的距离为5.
(1)分别确定反比例函数与一次函数的解析式;
(2)设一次函数与反比例函数图像的另一个交点为B ,试判断∠AOB(点O为平面直角坐标系原点)是锐角、直角还是钝角?并简单说明理由.
14. (12分)某蓄水池的排水管每小时排水飞12m3, 8h可将满池水全部排空.
(1)蓄水池的容积是多少?
(2)如果增加排水管,使每小时的排水量达到x(m3),那么将满池水排空所需的时间y(h)将如何变化?
(3)写出y与x之间的关系式;
(4)如果准备在6h内将满池水排空,那么每小时的排水量至少为多少?
(5)已知排水管每小时的最大排水量为24m3,那么最少多长时间可将满池水全部排空?
13.(l0分)在某一电路中,保持电压不变,电流I(安培)与电阻R(欧姆)成反比例.当电阻R=5欧姆时,电流 I=2安培.
(l)求I与R之间的函数关系式;
(2)当电流I= 0.5 安培时,求电阻R的值;
(3)如果电路中用电器的可变电阻逐渐增大,那么电路中的电流将如何变化?
(4)如果电路中用电器限制电流不得超过10安培,那么用电器的可变电阻应控制在什么范围内?
12.(8分)已知圆柱的侧面积是6πm2,若圆柱的底面半径为x(cm),高为ycm ).
(1)写出y关于x的函数解析式;
(2)完成下列表格:
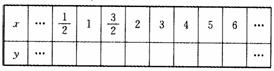
(3)在所给的平面直角坐标系中画出y关于x的函数图像.
11.(8分) 一定质量的氧气,其密度ρ(kg/m,)是它的体积v (m,)的反比例函数.当V=10m3 时甲=1.43kg/m.
(1)求ρ与v的函数关系式;
(2)求当V=2m3时,氧气的密度.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com