18．(6分)若函数y＝kx²+2(k+1)x+k－1与x 轴只有一个交点，求k 的值．

[提示]本题要分k＝0，k≠0两种情况讨论．

[解]当k＝0时，y＝2 x－1，是一次函数，此时，直线与x 轴必有一个交点．

当k≠0时，函数为二次函数，

此时，D ＝4(k+1)²－4 k(k－1)

＝12 k+4＝0．

∴　 k＝－．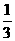

∴　 所求的k 值为0或－．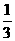

[点评]注意，当问题中未指明函数形式，而最高次项系数含字母时，要注意这个系数是否为0．函数图象与x 轴有一个交点包括两种情形：当函数是一次函数时，直线与x 轴必只有一个交点；当函数是二次函数时，在D ＝0的条件下，图象与x 轴只有一个交点．

17．(6分)已知y＝y₁+y₂，y₁ 与x 成正比例，y₂ 与x 成反比例，并且x＝1时y＝4，x＝2时y＝5，求当x＝4时y 的值．

[解]设y₁＝k₁x，y₂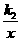＝，则y＝k₁x+．

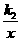把x＝1时y＝4，x＝2时y＝5分别代入上式，得

，

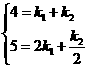解得

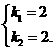
∴　 函数解析式为y＝2 x+．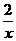

当x＝4时，y＝2×4+＝．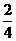

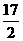∴　 所求的y 值为．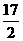

[点评]本题考查用待定系数法求函数解析式．关键在于正确设出y₁，y₂ 与x 的函数解析式．注意两个比例系数应分别用k₁，k₂ 表示出来，而不能仅用一个k 值表示．

16．某种火箭的飞机高度h(米)与发射后飞行的时间t(秒)之间的函数关系式是h＝－10 t²+20 t，经过_________秒，火箭发射后又回到地面．

[提示]火箭返回地面，即指飞行高度为0，则－10 t²+20 t＝0，故t＝0或t＝20．

[答案]20．

[点评]注意：t＝0应舍去的原因是此时火箭虽在地面，但未发射，而不是返回地面．

15．公民的月收入超过800元时，超过部分须依法缴纳个人收入调节税，当超过部分不足500元时，税率(即所纳税款占超过部分的百分数)相同．某人本月收入1260元，纳税23元，由此可得所纳税款y(元)与此人月收入x(元)800＜x＜1300间的函数关系为____________．

[提示]因1260－800＝460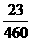，＝5%，故在800＜x＜1300时的税率为5%．

[答案]y＝5%(x－800)．

[点评]本题是与实际问题相关的函数关系式，解题时应注意并不是每个人月收入的全部都必须纳税，而是超过800元的部分才纳税，故列函数式时月收入x须减去800．

14．若一次函数y＝kx+b 的自变量x 的取值范围是－2≤x≤6，相应函数值y 的范围是－11≤y≤9，则函数解析式是___________．

[提示]当k＞0时，有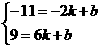，解得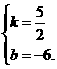

当k＜0时，有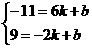，解得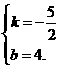

[答案]y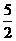＝x－6或y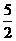＝－x+4．

[点评]因k 是待定字母，而k 的不同取值，导致线段分布象限不一样，自变量的取值与函数取值的对应关系也就不同．故本例要分k＞0时自变量最大值对应函数最大值，与k＜0时自变量最大值对应函数最小值两种情形讨论．

13．反比例函数y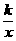＝的图象过点P(m，n)，其中m，n 是一元二次方程x²+kx+4＝0的两个根，那么P 点坐标是_____________．

[提示]P(m，n)在双曲线上，则k＝xy＝mn，又mn＝4，故k＝4．

[答案](－2，－2)．

[点评]本题是反比例函数、一元二次方程知识的综合应用．由题意得出k＝mn＝4是关键．

12．已知函数y＝x²－(2m+4)x+m²－10与x 轴的两个交点间的距离为2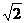，则m＝___________．

[提示]抛物线与x 轴两交点间距离可应用公式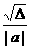来求．本题有

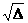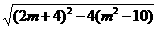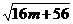＝＝＝2，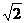

故m＝－3．

[答案]－3．

[点评]抛物线与x 轴两交点间距离的公式为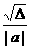，它有着广泛的应用．

11．正比例函数y＝k(k+1)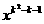的图象过第________象限．

[提示]由题意得k²－k－1＝1，解得k₁＝2，k₂＝－1(舍去)，则函数为y＝6 x．

[答案]一、三．

[点评]注意求出的k＝－1使比例系数为0，应舍去．

10．若点P(a－b，a)位于第二象限，那么点Q(a+3，ab)位于第_______象限．

[提示]由题意得a＞0，a－b＜0，则b＞0．故a+3＞0，ab＞0．

[答案]一．

9．函数y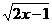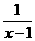＝+的自变量x 的取值范围是____________．

[提示]由2 x－1≥0，得x≥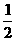；又x－1≠0，x≠1．综合可确定x 的取值范围．

[答案]x≥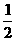，且x≠1．