
题目列表(包括答案和解析)
内容提要
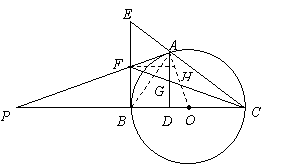
8、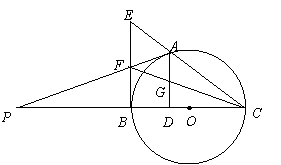 (2007四川成都)如图,
(2007四川成都)如图, 是以
是以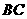 为直径的
为直径的 上一点,
上一点,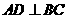 于点
于点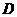 ,过点
,过点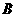 作
作 的切线,与
的切线,与 的延长线相交于点
的延长线相交于点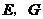 是
是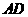 的中点,连结
的中点,连结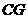 并延长与
并延长与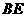 相交于点
相交于点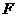 ,延长
,延长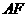 与
与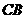 的延长线相交于点
的延长线相交于点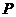 .
.
(1)求证: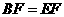 ;
;
(2)求证: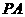 是
是 的切线;
的切线;
(3)若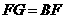 ,且
,且 的半径长为
的半径长为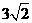 ,求
,求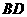 和
和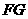 的长度.
的长度.
(1)证明: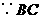 是
是 的直径,
的直径,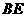 是
是 的切线,
的切线,
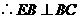 .
.
又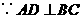 ,
,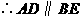 .
.
易证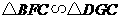 ,
,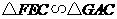 .
.
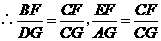 .
.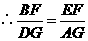 .
.
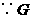 是
是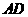 的中点,
的中点,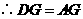 .
.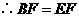 .
.
(2)证明:连结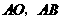 .
.
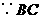 是
是 的直径,
的直径, .
.
在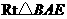 中,由(1),知
中,由(1),知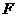 是斜边
是斜边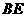 的中点,
的中点,
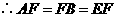 .
.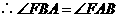 .
.
又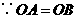 ,
,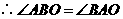 .
.
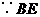 是
是 的切线,
的切线, .
.
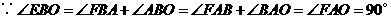 ,
,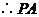 是
是 的切线.
的切线.
(3)解:过点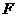 作
作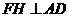 于点
于点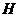 .
.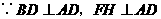 ,
,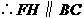 .
.
由(1),知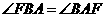 ,
,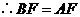 .
.
由已知,有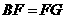 ,
,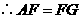 ,即
,即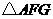 是等腰三角形.
是等腰三角形.
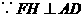 ,
,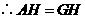 .
.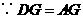 ,
,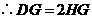 ,即
,即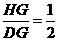 .
.
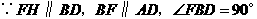 ,
,
 四边形
四边形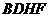 是矩形,
是矩形,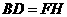 .
.
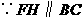 ,易证
,易证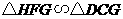 .
.
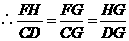 ,即
,即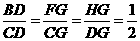 .
.
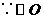 的半径长为
的半径长为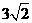 ,
,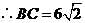 .
.
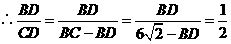 .解得
.解得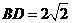 .
.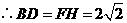 .
.
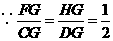 ,
,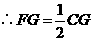 .
.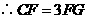 .
.
在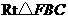 中,
中,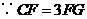 ,
,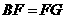 ,由勾股定理,得
,由勾股定理,得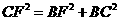 .
.
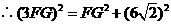 .解得
.解得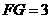 (负值舍去).
(负值舍去).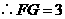 .
.
[或取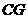 的中点
的中点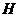 ,连结
,连结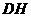 ,则
,则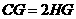 .易证
.易证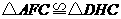 ,
,
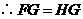 ,故
,故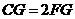 ,
,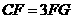 .
.
由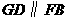 ,易知
,易知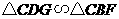 ,
,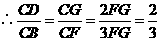 .
.
由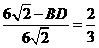 ,解得
,解得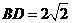 .
.
又在 中,由勾股定理,得
中,由勾股定理,得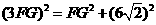 ,
,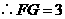 (舍去负值).]
(舍去负值).]
7、 (2007山东德州)如图12,
(2007山东德州)如图12, 是
是 的内接三角形,
的内接三角形,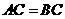 ,
,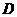 为
为 中
中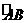 上一点,延长
上一点,延长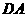 至点
至点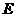 ,使
,使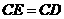 .
.
(1)求证: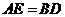 ;
;
(2)若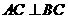 ,求证:
,求证: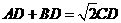 .
.
证明:(1)在 中,
中,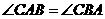 .
.
在 中,
中,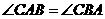 .
.
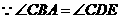 ,(同弧上的圆周角相等),
,(同弧上的圆周角相等),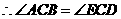 .
.
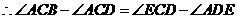 .
.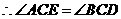 .
.
在 和
和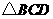 中,
中,

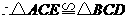 .
.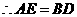 .
.
(2)若 .
.
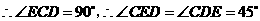 .
.
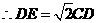 ,又
,又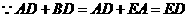
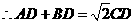
6、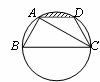 (2007山东临沂)如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10。
(2007山东临沂)如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10。
(1)求此圆的半径;
(2)求图中阴影部分的面积。

5、(2007福建福州)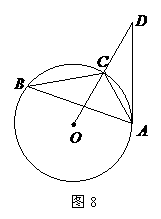 如图8,已知:
如图8,已知: 内接于
内接于 ,点
,点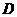 在
在 的延长线上,
的延长线上,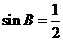 ,
,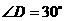 .
.
(1)求证: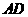 是
是 的切线;
的切线;
(2)若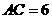 ,求
,求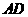 的长.
的长.
(1)证明:如图9,连结 .
.
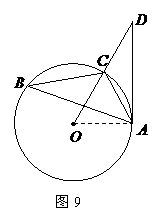
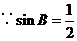 ,
,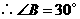 .
.
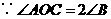 ,
, .
.
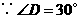 ,
,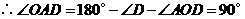 .
.
 是
是 的切线.
的切线.
(2)解: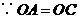 ,
,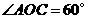 .
.
 是等边三角形,
是等边三角形,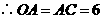 .
.
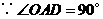 ,
,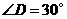 ,
,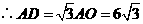 .
.
4、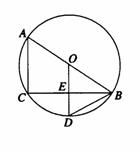 (2007山东枣庄)如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交
(2007山东枣庄)如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交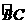 于D.
于D.
(1)请写出五个不同类型的正确结论;
(2)若BC=8,ED=2,求⊙O的半径.
解:(1)不同类型的正确结论有:
①BC=CE ;②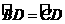 = ③∠BED=90°④∠BOD=∠A;⑤AC∥OD,⑥AC⊥BC;
= ③∠BED=90°④∠BOD=∠A;⑤AC∥OD,⑥AC⊥BC;
⑦OE2+BE2=OB2;⑧S△ABC=BC·OE;⑨△BOD是等腰三角形,⑩△BOE∽△BAC;等
(2)∵OD⊥BC, ∴BE=CE=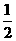 BC=4.
BC=4.
设⊙O的半径为R,则OE=OD-DE=R-2.
在Rt△OEB中,由勾股定理得 OE2+BE2=OB2,即(R-2)2+42=R2.
解得R=5.∴⊙O的半径为5.
3、(2007山东济宁)如图,AB为⊙O的直径,弦CD⊥AB于点M,过点B作BE∥CD,交AC的延长线于点E,连结BC。
(1)求证:BE为⊙O的切线;
(2)如果CD=6,tan∠BCD=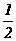 ,求⊙O的直径。
,求⊙O的直径。

2、(2007浙江金华)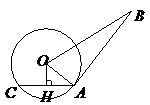 如图,
如图,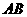 是
是 的切线,
的切线, 为切点,
为切点, 是
是 的弦,过
的弦,过 作
作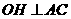 于点
于点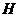 .若
.若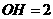 ,
,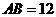 ,
,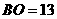 .
.
求:(1) 的半径;
的半径;
(2)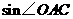 的值;
的值;
(3)弦 的长(结果保留两个有效数字).
的长(结果保留两个有效数字).
解:(1)
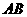 是
是 的切线,
的切线,
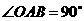 ,
,
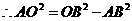 ,
,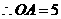 .
.
(2)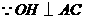 ,
,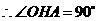 ,
,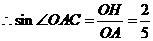 .
.
(3)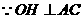 ,
,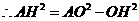 ,
,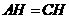 ,
,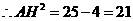 ,
,
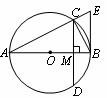
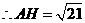 ,
,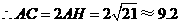 .
.
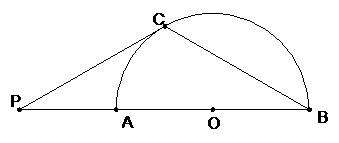
1、(2007浙江温州)如图,点P在 的直径BA的延长线上,AB=2PA,PC切
的直径BA的延长线上,AB=2PA,PC切 于点C,连结BC。
于点C,连结BC。
(1)求 的正弦值;
的正弦值;
 (2)若
(2)若 的半径r=2cm,求BC的长度。
的半径r=2cm,求BC的长度。
解:(1)连结OC,因为PC切 于点C,
于点C,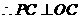
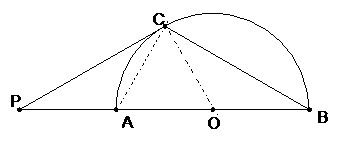
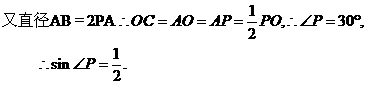
(或:在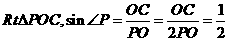 )
)
(2)连结AC,由AB是直
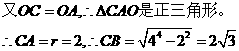
8、 (2007四川成都)如图,已知
(2007四川成都)如图,已知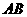 是
是 的直径,弦
的直径,弦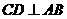 ,
,
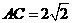 ,
,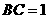 ,那么
,那么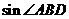 的值是
的值是
.
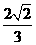
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com