
题目列表(包括答案和解析)
5.已知关于x的一元二次方程2x2+4x+m=0。
(1 )若x=1是方程的一个根,求方程的另一个根;
(2) 若x1、x2是方程的两个不同的实数根,且x1和x2满足:x12+x22+2x1x2―x12x22=0,求m的值。
[解](1)―3 (2)m=±4。
4.已知:关于x的方程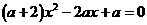 有两个不相等的实数根
有两个不相等的实数根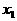 和
和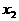 ,并且抛物线
,并且抛物线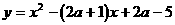 与x轴的两个交点分别位于点(2,0)的两旁。
与x轴的两个交点分别位于点(2,0)的两旁。
(1)求实数a的取值范围;
(2)当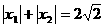 时,求a的值。
时,求a的值。
[解](1)解法一:∵关于x的方程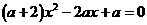 有两个不相等的实数根
有两个不相等的实数根
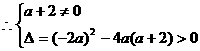
解得: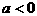 ,且
,且
设抛物线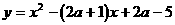 与x轴的两个交点的坐标分别为
与x轴的两个交点的坐标分别为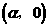 、
、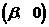 ,且
,且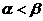
∴α、β是关于x的方程 的两个不相等的实数根
的两个不相等的实数根
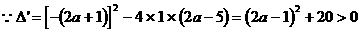
∴a为任意实数 <2>
由根与系数关系得: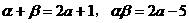
∵抛物线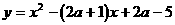 与x轴的两个交点分别位于点(2,0)的两旁
与x轴的两个交点分别位于点(2,0)的两旁
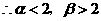
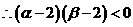
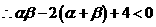
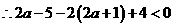
解得:
由<1>、<2>、<3>得 a的取值范围是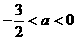
解法二:同解法一,得: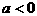 ,且
,且
∵抛物线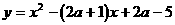 与x轴的两个交点分别位于点(2,0)两旁,且抛物线的开口向上
与x轴的两个交点分别位于点(2,0)两旁,且抛物线的开口向上
∴当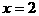 时,
时,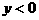
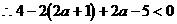
解得: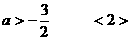
由<1>、<2>得 a的取值范围是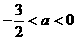
(2)解:∵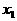 和
和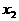 是关于x的方程
是关于x的方程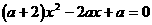 的两个不相等的实数根
的两个不相等的实数根
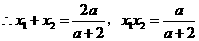
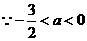

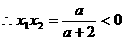 不妨设
不妨设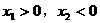
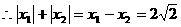
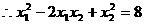 ,即
,即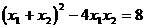
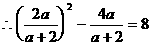
解这个方程,得: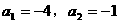
经检验,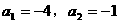 都是方程
都是方程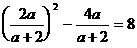 的根
的根
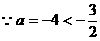 ,舍去
,舍去
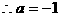 为所求
为所求
3.已知: x1、x2是关于x的方程x2+(2a-1)x+a2=0的两个实数根
且(x1+2)(x2+2)=11,求a的值。
[解]∵x1、x2是方程x2+(2a-1)x+a2=0的两个实数根,
∴x1+x2=1-2a,x1﹒x2=a2
∵(x1+2)(x2+2)=11, ∴x1x2+2(x1+x2)+4=11
∴a2+2(1-2a)-7=0,即a2-4a-5=0。
解得a=-1,或a=5。
又∵Δ=(2a-1)2-4a2=1-4a≥0, ∴a≤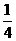 。 ∴a=5不合题意,舍去。
。 ∴a=5不合题意,舍去。
∴a=-1
2.已知关于 的方程
的方程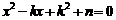 有两个不相等的实数根
有两个不相等的实数根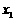 、
、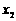 ,且
,且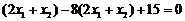 .
.
(1)求证: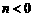 ; (2)试用
; (2)试用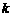 的代数式表示
的代数式表示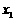 ;
;
(3)当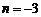 时,求
时,求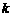 的值.
的值.
[解]⑴证明:∵关于 的方程
的方程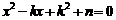 有两个不相等的实数根,
有两个不相等的实数根,
∴△=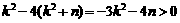 ,∴
,∴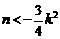 .
.
又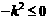 ,∴
,∴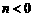 .
.
⑵ 或
或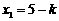
(3)当 时,k=1.当
时,k=1.当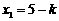 时,k不存在.所求的k的值为1.
时,k不存在.所求的k的值为1.
1.已知关于x的方程 kx2-2 (k+1) x+k-1=0 有两个不相等的实数根,
(1) 求k的取值范围;
(2) 是否存在实数k,使此方程的两个实数根的倒数和等于0 ?若存在,求出k的值;若不存在,说明理由.
[解]. (1) ∵方程有两个不相等的实数根,∴Δ=[-2(k+1)]2-4k(k-1)>0,且k≠0,解得k>-1,且k≠0 .即k的取值范围是k>-1,且k≠0 .
(2) 假设存在实数k,使得方程的两个实数根x1 , x2的倒数和为0.
则x1 ,x2不为0,且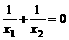 ,即
,即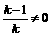 ,且
,且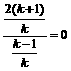 ,解得k=-1 .
,解得k=-1 .
而k=-1 与方程有两个不相等实根的条件k>-1,且k≠0矛盾,
故使方程的两个实数根的倒数和为0的实数k不存在 .
6.解方程,判别方程2y2―8y+5=0的根的情况是___有两个不相等的正实数_________。
5.已知关于x的方程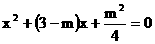 有两个不相等的实数根,那么m的最大整数值是 1 。
有两个不相等的实数根,那么m的最大整数值是 1 。
4.若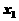 、
、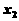 为方程
为方程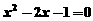 的两根,则
的两根,则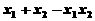 = 3
= 3
3.如果关于x的方程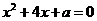 有两个相等的实数根,那么a= 4
有两个相等的实数根,那么a= 4
2.设x1、x2是方程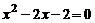 的两个实数根,则x1+x2=__2___;x1·x2=__-2___.
的两个实数根,则x1+x2=__2___;x1·x2=__-2___.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com