
题目列表(包括答案和解析)
3、(2007江苏苏州)方程组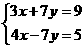 的解是 ( )D
的解是 ( )D
A.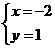 B.
B.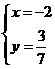 C.
C.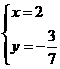 D.
D.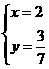
2、(2007浙江丽水)方程组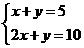 ,由②
,由②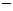 ①,得正确的方程是( )B
①,得正确的方程是( )B
A. 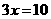 B.
B. 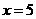 C.
C. 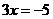 D.
D. 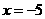
1、(2007陕西课改)中国人民银行宣布,从2007年6月5日起,上调人民币存款利率,一年定期存款利率上调到3.06%.某人于2007年6月5日存入定期为1年的人民币5000元(到期后银行将扣除20%的利息锐).设到期后银行应向储户支付现金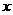 元,则所列方程正确的是( )C
元,则所列方程正确的是( )C
A.
B.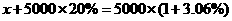
C.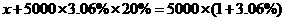
D.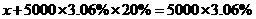
9、(湖北荆门)如图1,在平面直角坐标系中,有一张矩形纸片OABC,已知O(0,0),A(4,0),C(0,3),点P是OA边上的动点(与点O、A不重合).现将△PAB沿PB翻折,得到△PDB;再在OC边上选取适当的点E,将△POE沿PE翻折,得到△PFE,并使直线PD、PF重合.
(1)设P(x,0),E(0,y),求y关于x的函数关系式,并求y的最大值;
(2)如图2,若翻折后点D落在BC边上,求过点P、B、E的抛物线的函数关系式;
(3)在(2)的情况下,在该抛物线上是否存在点Q,使△PEQ是以PE为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q的坐标.
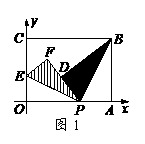
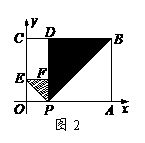
解:(1)由已知PB平分∠APD,PE平分∠OPF,且PD、PF重合,则∠BPE=90°.∴∠OPE+∠APB=90°.又∠APB+∠ABP=90°,∴∠OPE=∠PBA.
∴Rt△POE∽Rt△BPA.……………………………………………………………………2分
∴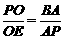 .即
.即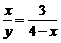 .∴y=
.∴y=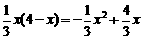 (0<x<4).
(0<x<4).
且当x=2时,y有最大值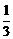 .………………………………………………………………4分
.………………………………………………………………4分
(2)由已知,△PAB、△POE均为等腰三角形,可得P(1,0),E(0,1),B(4,3).……6分
设过此三点的抛物线为y=ax2+bx+c,则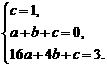 ∴
∴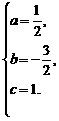
y=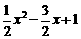 .……………………………………………………………………………8分
.……………………………………………………………………………8分
(3)由(2)知∠EPB=90°,即点Q与点B重合时满足条件.………………………………9分
直线PB为y=x-1,与y轴交于点(0,-1).
将PB向上平移2个单位则过点E(0,1),
∴该直线为y=x+1.………………………………………………………………………10分
由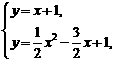 得
得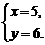 ∴Q(5,6).
∴Q(5,6).
故该抛物线上存在两点Q(4,3)、(5,6)满足条件.……………………………………12分

8、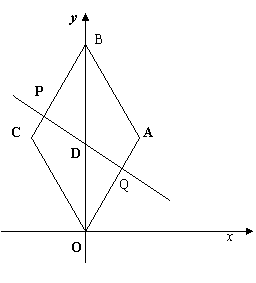 (湖北黄岗)已知:如图,在平面直角坐标系中,四边形ABCO是菱形,且∠AOC=60°,点B的坐标是
(湖北黄岗)已知:如图,在平面直角坐标系中,四边形ABCO是菱形,且∠AOC=60°,点B的坐标是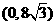 ,点P从点C开始以每秒1个单位长度的速度在线段CB上向点B移动,设
,点P从点C开始以每秒1个单位长度的速度在线段CB上向点B移动,设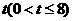 秒后,直线PQ交OB于点D.
秒后,直线PQ交OB于点D.
(1)求∠AOB的度数及线段OA的长;
(2)求经过A,B,C三点的抛物线的解析式;
(3)当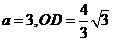 时,求t的值及此时直线PQ的解析式;
时,求t的值及此时直线PQ的解析式;
(4)当a为何值时,以O,P,Q,D为顶点的三角形与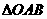 相似?当a 为何值时,以O,P,Q,D为顶点的三角形与
相似?当a 为何值时,以O,P,Q,D为顶点的三角形与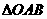 不相似?请给出你的结论,并加以证明.
不相似?请给出你的结论,并加以证明.
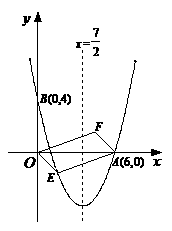
7、(河南)如图,对称轴为直线x=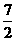 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).
(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形,求四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)①当四边形OEAF的面积为24时,请判断OEAF是否为菱形?
②是否存在点E,使四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
6、(贵阳)如图14,从一个直径是2的圆形铁皮中剪下一个圆心角为 的扇形.
的扇形.
(1)求这个扇形的面积(结果保留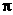 ).(3分)
).(3分)
(2)在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由.(4分)
(3)当 的半径
的半径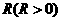 为任意值时,(2)中的结论是否仍然成立?请说明理由.(5分)
为任意值时,(2)中的结论是否仍然成立?请说明理由.(5分)
解:(1)连接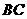 ,由勾股定理求得:
,由勾股定理求得:
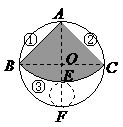
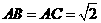 ·································································· 1分
·································································· 1分
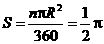 ································································· 2分
································································· 2分
(2)连接 并延长,与弧
并延长,与弧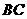 和
和 交于
交于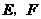 ,
,
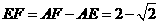 ····························································································· 1分
····························································································· 1分
弧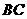 的长:
的长: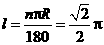 ······················································································ 2分
······················································································ 2分
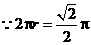
 圆锥的底面直径为:
圆锥的底面直径为: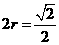 ··················································································· 3分
··················································································· 3分
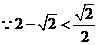 ,
, 不能在余料③中剪出一个圆作为底面与此扇形围成圆锥.·············· 4分
不能在余料③中剪出一个圆作为底面与此扇形围成圆锥.·············· 4分
(3)由勾股定理求得: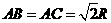
弧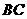 的长:
的长: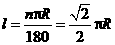 ···················································································· 1分
···················································································· 1分
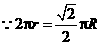
 圆锥的底面直径为:
圆锥的底面直径为: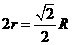 ················································································ 2分
················································································ 2分
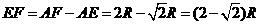
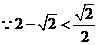 且
且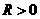
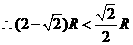 ···································································································· 3分
···································································································· 3分
即无论半径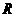 为何值,
为何值,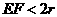 ··················································································· 4分
··················································································· 4分
 不能在余料③中剪出一个圆作为底面与此扇形围成圆锥.
不能在余料③中剪出一个圆作为底面与此扇形围成圆锥.
5、(甘肃陇南)如图,抛物线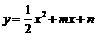 交
交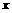 轴于A、B两点,交
轴于A、B两点,交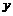 轴于点C,点P是它的
轴于点C,点P是它的
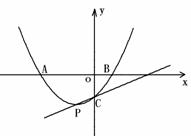 顶点,点A的横坐标是
顶点,点A的横坐标是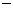 3,点B的横坐标是1.
3,点B的横坐标是1.
(1)求 、
、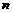 的值;
的值;
(2)求直线PC的解析式;
(3)请探究以点A为圆心、直径为5的圆与直线
PC的位置关系,并说明理由.(参考数: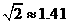 ,
,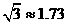 ,
,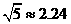 )
)
解: (1)由已知条件可知: 抛物线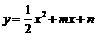 经过A(-3,0)、B(1,0)两点.
经过A(-3,0)、B(1,0)两点.
∴ 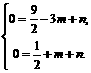 ……………………………………2分
……………………………………2分
解得 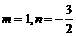 .
………………………3分
.
………………………3分
(2) ∵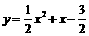 , ∴ P(-1,-2),C
, ∴ P(-1,-2),C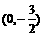 . …………………4分
. …………………4分
设直线PC的解析式是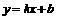 ,则
,则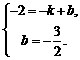 解得
解得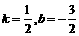 .
.
∴ 直线PC的解析式是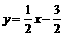 .
…………………………6分
.
…………………………6分
说明:只要求对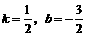 ,不写最后一步,不扣分.
,不写最后一步,不扣分.
(3) 如图,过点A作AE⊥PC,垂足为E.
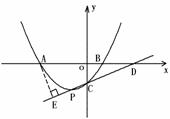 设直线PC与
设直线PC与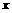 轴交于点D,则点D的坐标为(3,0). ………………………7分
轴交于点D,则点D的坐标为(3,0). ………………………7分
在Rt△OCD中,∵ OC=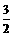 ,
,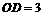 ,
,
∴ 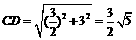 .
…………8分
.
…………8分
∵ OA=3,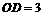 ,∴AD=6. …………9分
,∴AD=6. …………9分
∵ ∠COD=∠AED=90o,∠CDO公用,
∴ △COD∽△AED. ……………10分
∴ 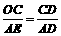 , 即
, 即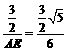 . ∴
. ∴ 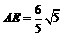 . …………………11分
. …………………11分
∵ 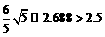 ,
,
∴ 以点A为圆心、直径为5的圆与直线PC相离. …………12分
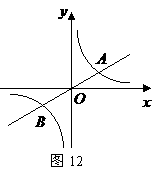
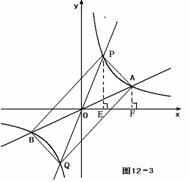
4、(福州)如图12,已知直线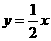 与双曲线
与双曲线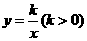 交于
交于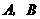 两点,且点
两点,且点 的横坐标为
的横坐标为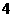 .
.
(1)求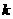 的值;
的值;
(2)若双曲线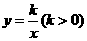 上一点
上一点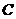 的纵坐标为8,求
的纵坐标为8,求 的面积;
的面积;
 (3)过原点
(3)过原点 的另一条直线
的另一条直线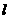 交双曲线
交双曲线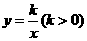 于
于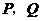 两点(
两点(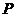 点在第一象限),若由点
点在第一象限),若由点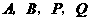 为顶点组成的四边形面积为
为顶点组成的四边形面积为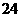 ,求点
,求点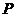 的坐标.
的坐标.
解:(1)∵点A横坐标为4 , ∴当 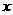 = 4时,
= 4时,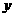 = 2 .
= 2 .
∴ 点A的坐标为( 4,2 ).
∵ 点A是直线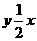 与双曲线
与双曲线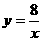 (k>0)的交点 ,
(k>0)的交点 ,
∴ k = 4 ×2 = 8 .
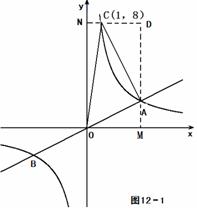 (2) 解法一:如图12-1,
(2) 解法一:如图12-1,
∵ 点C在双曲线 上,当
上,当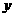 = 8时,
= 8时,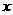 = 1
= 1
∴ 点C的坐标为 ( 1, 8 ) .
过点A、C分别做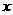 轴、
轴、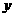 轴的垂线,垂足为M、N,得矩形DMON .
轴的垂线,垂足为M、N,得矩形DMON .
S矩形ONDM= 32 , S△ONC = 4 , S△CDA = 9, S△OAM = 4 .
S△AOC= S矩形ONDM - S△ONC - S△CDA - S△OAM = 32 - 4 - 9 - 4 = 15 .
解法二:如图12-2,
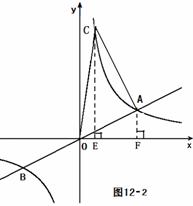 过点
C、A分别做
过点
C、A分别做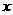 轴的垂线,垂足为E、F,
轴的垂线,垂足为E、F,
∵ 点C在双曲线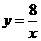 上,当
上,当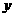 = 8时,
= 8时,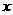 = 1 .
= 1 .
∴ 点C的坐标为 ( 1, 8 ).
∵ 点C、A都在双曲线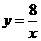 上 ,
上 ,
∴ S△COE = S△AOF = 4 。
∴ S△COE + S梯形CEFA = S△COA + S△AOF .
∴ S△COA = S梯形CEFA .
∵ S梯形CEFA = 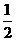 ×(2+8)×3 = 15 ,
×(2+8)×3 = 15 ,
∴ S△COA = 15 .
(3)∵ 反比例函数图象是关于原点O的中心对称图形 ,
∴ OP=OQ,OA=OB .
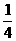 ∴ 四边形APBQ是平行四边形 .
∴ 四边形APBQ是平行四边形 .
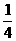 ∴ S△POA = S平行四边形APBQ = ×24 = 6 .
∴ S△POA = S平行四边形APBQ = ×24 = 6 .
设点P的横坐标为 (
( > 0且
> 0且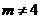 ),
),
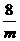 得P (
得P (  , ) .
, ) .
过点P、A分别做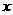 轴的垂线,垂足为E、F,
轴的垂线,垂足为E、F,
∵ 点P、A在双曲线上,∴S△POE = S△AOF = 4 .
若0< <4,如图12-3,
<4,如图12-3,
∵ S△POE + S梯形PEFA = S△POA + S△AOF,
∴ S梯形PEFA = S△POA = 6 .
∴ 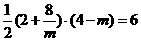 .
.
解得 = 2,
= 2, = - 8(舍去) .
= - 8(舍去) .
 ∴ P(2,4).
∴ P(2,4).
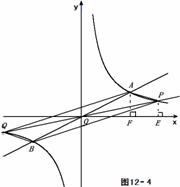
若  > 4,如图12-4,
> 4,如图12-4,
∵ S△AOF+ S梯形AFEP = S△AOP + S△POE,
∴ S梯形PEFA = S△POA = 6 .
∴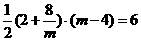 ,
,
解得 = 8,
= 8, = - 2 (舍去) .
= - 2 (舍去) .
∴ P(8,1).
∴ 点P的坐标是P(2,4)或P(8,1).
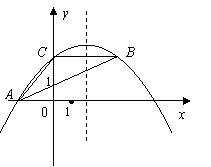
3、(福建龙岩)如图,抛物线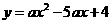 经过
经过 的三个顶点,已知
的三个顶点,已知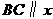 轴,点
轴,点 在
在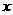 轴上,点
轴上,点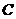 在
在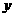 轴上,且
轴上,且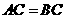 .
.
(1)求抛物线的对称轴;
(2)写出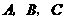 三点的坐标并求抛物线的解析式;
三点的坐标并求抛物线的解析式;
(3)探究:若点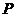 是抛物线对称轴上且在
是抛物线对称轴上且在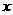 轴下方的动点,是否存在
轴下方的动点,是否存在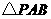 是等腰三角形.若存在,求出所有符合条件的点
是等腰三角形.若存在,求出所有符合条件的点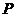 坐标;不存在,请说明理由.
坐标;不存在,请说明理由.
解:(1)抛物线的对称轴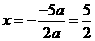 ………2分
………2分
(2)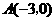
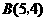
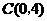 …………5分
…………5分
把点 坐标代入
坐标代入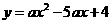 中,解得
中,解得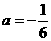 ………6分
………6分
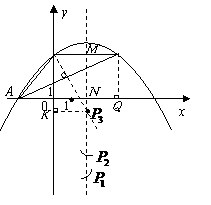
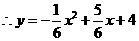 …………………………………………7分
…………………………………………7分
(3)存在符合条件的点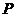 共有3个.以下分三类情形探索.
共有3个.以下分三类情形探索.
设抛物线对称轴与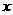 轴交于
轴交于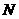 ,与
,与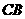 交于
交于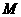 .
.
过点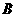 作
作 轴于
轴于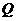 ,易得
,易得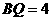 ,
,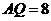 ,
,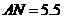 ,
,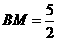
①
以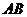 为腰且顶角为角
为腰且顶角为角 的
的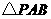 有1个:
有1个: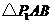 .
.
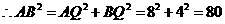 ······································································ 8分
······································································ 8分
在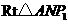 中,
中,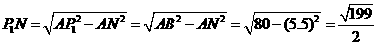
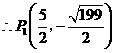 ································································································· 9分
································································································· 9分
②以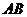 为腰且顶角为角
为腰且顶角为角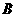 的
的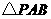 有1个:
有1个: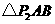 .
.
在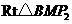 中,
中,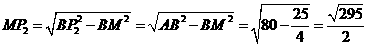 ···· 10分
···· 10分
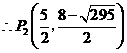 ····························································································· 11分
····························································································· 11分
③以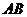 为底,顶角为角
为底,顶角为角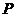 的
的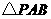 有1个,即
有1个,即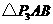 .
.
画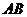 的垂直平分线交抛物线对称轴于
的垂直平分线交抛物线对称轴于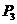 ,此时平分线必过等腰
,此时平分线必过等腰 的顶点
的顶点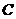 .
.
过点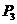 作
作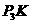 垂直
垂直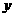 轴,垂足为
轴,垂足为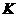 ,显然
,显然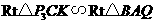 .
.
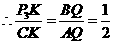 .
.
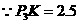
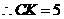 于是
于是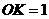 ······························································ 13分
······························································ 13分
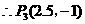 ······································································································· 14分
······································································································· 14分
注:第(3)小题中,只写出点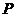 的坐标,无任何说明者不得分.
的坐标,无任何说明者不得分.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com