
题目列表(包括答案和解析)
10. 解答: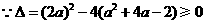
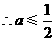 又
又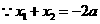 ,
,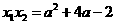
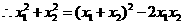
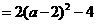
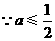
 当
当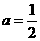 时,
时,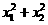 的值最小
的值最小
此时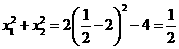 ,即最小值为
,即最小值为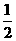 .
.
9. 解法一:设矩形温室的宽为xm,则长为2xm.根据题意,得
(x-2)·(2x-4)=288. …………………………………………………4分
解这个方程,得
x1=-10(不合题意,舍去),x2=14……………………………………6分
所以x=14,2x=2×14=28.
答:当矩形温室的长为28m,宽为14m时,蔬菜种植区域的面积是288m2.
……………………………………………………………………………7分
解法二:设矩形温室的长为xm,则宽为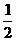 xm,根据题意,得
xm,根据题意,得
(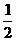 x-2)·(x-4)=288.
………………………………………………4分
x-2)·(x-4)=288.
………………………………………………4分
解这个方程,得
x1=-20(不合题意,舍去),x2=28. ……………………………………6分
所以x=28, 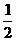 x=
x=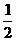 ×28=14.
×28=14.
答:当矩形温室的长为28m,宽为14m时,蔬菜种植区域的面积是288m2.
……………………………………………………………………………7分
8. 解:⑴设所围矩形ABCD的长AB为x米,则宽AD为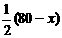 米.
米.
依题意,得 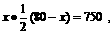
即,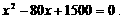
解此方程,得 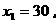
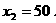
∵墙的长度不超过45m,∴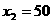 不合题意,应舍去.
不合题意,应舍去.
当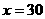 时,
时,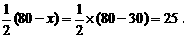
所以,当所围矩形的长为30m、宽为25m时,能使矩形的面积为750m2.
⑵不能.因为由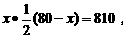 得
得
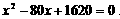
又∵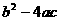 =(-80)2-4×1×1620=-80<0,
=(-80)2-4×1×1620=-80<0,
∴上述方程没有实数根.
因此,不能使所围矩形场地的面积为810m2
7. 解:由题意,△=(-4)2-4(m-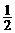 )=0
)=0
即16-4m+2=0,m=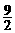 .
.
当m=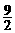 时,方程有两个相等的实数根x1=x2=2.
时,方程有两个相等的实数根x1=x2=2.
6. 解: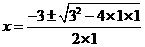
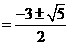
5. 解:(1)设A市投资“改水工程”年平均增长率是x,则
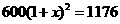
解之,得x=0.4或x=-2.4(不合题意,舍去)
所以,A市三年共投资“改水工程”2616万元.
4. 解法一:因为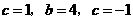 ,所以
,所以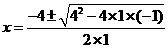 .·················· 3分
.·················· 3分
即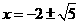 .所以,原方程的根为
.所以,原方程的根为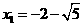 ,
,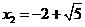 .························· 6分
.························· 6分
解法二:配方,得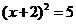 .··················································································· 2分
.··················································································· 2分
直接开平方,得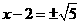 .····················································································· 4分
.····················································································· 4分
所以,原方程的根为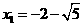 ,
,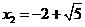 . 6分
. 6分
3. 解: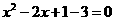 ………………1分
………………1分
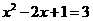 ………………2分
………………2分
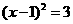 ………………3分
………………3分
∴x-1=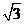 或x-1=-
或x-1=-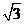 ………………4分
………………4分
∴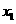 =1+
=1+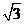 ,
,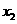 =1-
=1-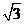 ………………6分
………………6分
2. x1=2 x2=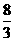
1. 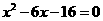
解: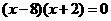 ·································································································· 3分
·································································································· 3分
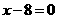 或
或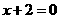 ····································································································· 5分
····································································································· 5分
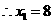 ,
,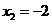 ······································································································· 6分
······································································································· 6分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com