
题目列表(包括答案和解析)
14.  解:(1)由题意可知,
解:(1)由题意可知,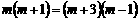 .
.
解,得 m=3. ………………………………3分
∴ A(3,4),B(6,2);
∴ k=4×3=12. ……………………………4分
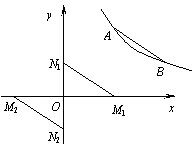
(2)存在两种情况,如图:
①当M点在x轴的正半轴上,N点在y轴的正半轴
上时,设M1点坐标为(x1,0),N1点坐标为(0,y1).
∵ 四边形AN1M1B为平行四边形,
∴ 线段N1M1可看作由线段AB向左平移3个单位,
再向下平移2个单位得到的(也可看作向下平移2个单位,再向左平移3个单位得到的).
由(1)知A点坐标为(3,4),B点坐标为(6,2),
∴ N1点坐标为(0,4-2),即N1(0,2); ………………………………5分
M1点坐标为(6-3,0),即M1(3,0). ………………………………6分
设直线M1N1的函数表达式为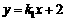 ,把x=3,y=0代入,解得
,把x=3,y=0代入,解得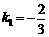 .
.
∴ 直线M1N1的函数表达式为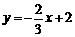 . ……………………………………8分
. ……………………………………8分
②当M点在x轴的负半轴上,N点在y轴的负半轴上时,设M2点坐标为(x2,0),N2点坐标为(0,y2).
∵ AB∥N1M1,AB∥M2N2,AB=N1M1,AB=M2N2,
∴ N1M1∥M2N2,N1M1=M2N2.
∴ 线段M2N2与线段N1M1关于原点O成中心对称.
∴ M2点坐标为(-3,0),N2点坐标为(0,-2). ………………………9分
设直线M2N2的函数表达式为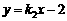 ,把x=-3,y=0代入,解得
,把x=-3,y=0代入,解得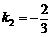 ,
,
∴ 直线M2N2的函数表达式为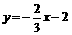 .
.
所以,直线MN的函数表达式为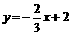 或
或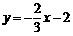 . ………………11分
. ………………11分
(3)选做题:(9,2),(4,5). ………………………………………………2分
13. 解:(1)分别过D,C两点作DG⊥AB于点G,CH⊥AB于点H. ……………1分
∵ AB∥CD,
∴ DG=CH,DG∥CH.
∴ 四边形DGHC为矩形,GH=CD=1.
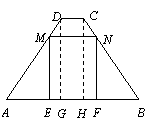 ∵ DG=CH,AD=BC,∠AGD=∠BHC=90°,
∵ DG=CH,AD=BC,∠AGD=∠BHC=90°,
∴ △AGD≌△BHC(HL).
∴ AG=BH=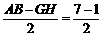 =3. ………2分
=3. ………2分
∵ 在Rt△AGD中,AG=3,AD=5,
∴ DG=4.
∴ 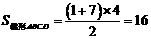 . ………………………………………………3分
. ………………………………………………3分
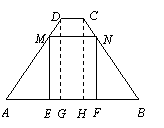 (2)∵ MN∥AB,ME⊥AB,NF⊥AB,
(2)∵ MN∥AB,ME⊥AB,NF⊥AB,
∴ ME=NF,ME∥NF.
∴ 四边形MEFN为矩形.
∵ AB∥CD,AD=BC,
∴ ∠A=∠B.
∵ ME=NF,∠MEA=∠NFB=90°,
∴ △MEA≌△NFB(AAS).
∴ AE=BF. ……………………4分
设AE=x,则EF=7-2x. ……………5分
∵ ∠A=∠A,∠MEA=∠DGA=90°,
∴ △MEA∽△DGA.
∴ 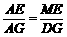 .
.
∴ ME=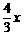 .
…………………………………………………………6分
.
…………………………………………………………6分
∴ 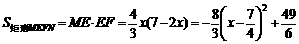 . ……………………8分
. ……………………8分
当x=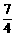 时,ME=
时,ME=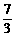 <4,∴四边形MEFN面积的最大值为
<4,∴四边形MEFN面积的最大值为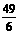 .……………9分
.……………9分
(3)能. ……………………………………………………………………10分
由(2)可知,设AE=x,则EF=7-2x,ME=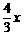 .
.
若四边形MEFN为正方形,则ME=EF.
即 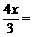 7-2x.解,得
7-2x.解,得 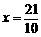 . ……………………………………………11分
. ……………………………………………11分
∴ EF=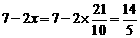 <4.
<4.
∴ 四边形MEFN能为正方形,其面积为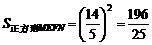 .
.
12. 解:(1)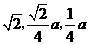 .····················································································· 3分
.····················································································· 3分
(2)相等,比值为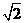 .················· 5分(无“相等”不扣分有“相等”,比值错给1分)
.················· 5分(无“相等”不扣分有“相等”,比值错给1分)
(3)设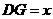 ,
,
在矩形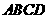 中,
中,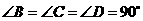 ,
,
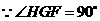 ,
,
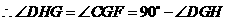 ,
,
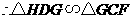 ,
,
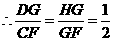 ,
,
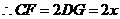 .···································································································· 6分
.···································································································· 6分
同理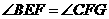 .
.
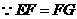 ,
,
 ,
,
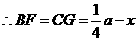 .······························································································· 7分
.······························································································· 7分
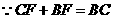 ,
,
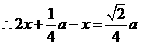 ,······························································································ 8分
,······························································································ 8分
解得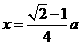 .
.
即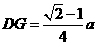 .······································································································ 9分
.······································································································ 9分
(4)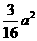 ,·············································································································· 10分
,·············································································································· 10分
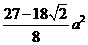 . 12分
. 12分
11. 解:(1)设 地经杭州湾跨海大桥到宁波港的路程为
地经杭州湾跨海大桥到宁波港的路程为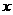 千米,
千米,
由题意得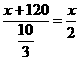 ,································································································ 2分
,································································································ 2分
解得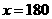 .
.
 地经杭州湾跨海大桥到宁波港的路程为180千米.················································· 4分
地经杭州湾跨海大桥到宁波港的路程为180千米.················································· 4分
(2)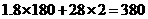 (元),
(元),
 该车货物从
该车货物从 地经杭州湾跨海大桥到宁波港的运输费用为380元.···························· 6分
地经杭州湾跨海大桥到宁波港的运输费用为380元.···························· 6分
(3)设这批货物有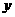 车,
车,
由题意得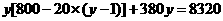 ,···························································· 8分
,···························································· 8分
整理得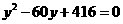 ,
,
解得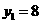 ,
,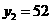 (不合题意,舍去),································································ 9分
(不合题意,舍去),································································ 9分
 这批货物有8车.···································································································· 10分
这批货物有8车.···································································································· 10分
10.



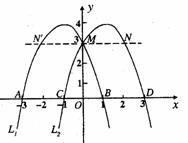
9.


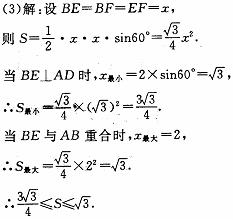
8. 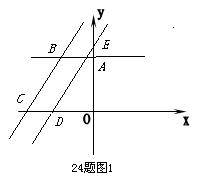
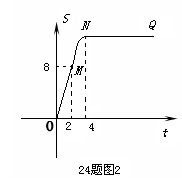 解:
解:
(1)①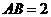 ……………………………………………………………………………2分
……………………………………………………………………………2分
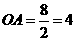 ,
,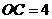 ,S梯形OABC=12 ……………………………………………2分
,S梯形OABC=12 ……………………………………………2分
②当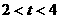 时,
时,
直角梯形OABC被直线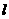 扫过的面积=直角梯形OABC面积-直角三角开DOE面积
扫过的面积=直角梯形OABC面积-直角三角开DOE面积
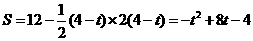 …………………………………………4分
…………………………………………4分
(2) 存在 ……………………………………………………………………………………1分
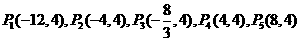 …(每个点对各得1分)……5分
…(每个点对各得1分)……5分
对于第(2)题我们提供如下详细解答(评分无此要求).下面提供参考解法二:
①
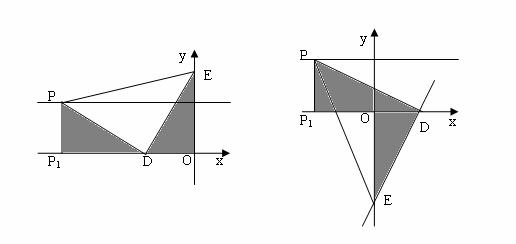 以点D为直角顶点,作
以点D为直角顶点,作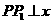 轴
轴

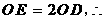 设
设 .
.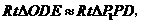 (图示阴影)
(图示阴影)

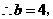
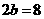 ,在上面二图中分别可得到
,在上面二图中分别可得到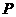 点的生标为P(-12,4)、P(-4,4)
点的生标为P(-12,4)、P(-4,4)
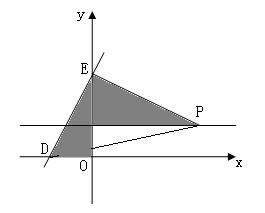
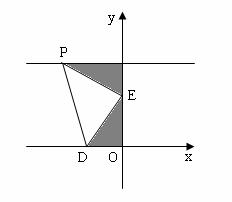 E点在0点与A点之间不可能;
E点在0点与A点之间不可能;
② 以点E为直角顶点
同理在②二图中分别可得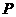 点的生标为P(-
点的生标为P(-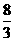 ,4)、P(8,4)E点在0点下方不可能.
,4)、P(8,4)E点在0点下方不可能.
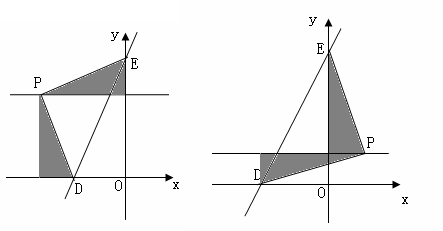 以点P为直角顶点
以点P为直角顶点
同理在③二图中分别可得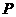 点的生标为P(-4,4)(与①情形二重合舍去)、P(4,4),
点的生标为P(-4,4)(与①情形二重合舍去)、P(4,4),
E点在A点下方不可能.
综上可得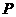 点的生标共5个解,分别为P(-12,4)、P(-4,4)、P(-
点的生标共5个解,分别为P(-12,4)、P(-4,4)、P(-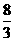 ,4)、
,4)、
P(8,4)、P(4,4).
下面提供参考解法二:
以直角进行分类进行讨论(分三类):
第一类如上解法⑴中所示图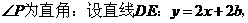
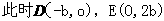
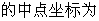
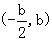 ,直线
,直线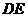 的中垂线方程:
的中垂线方程: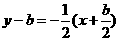 ,令
,令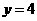 得
得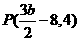 .由已知可得
.由已知可得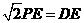 即
即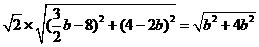 化简得
化简得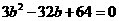 解得
解得 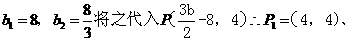
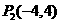 ;
;
第二类如上解法②中所示图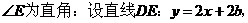
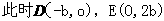
,直线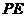 的方程:
的方程: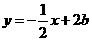 ,令
,令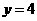 得
得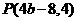 .由已知可得
.由已知可得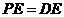 即
即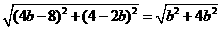 化简得
化简得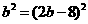 解之得 ,
解之得 ,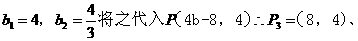
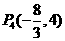
第三类如上解法③中所示图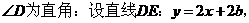
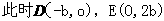
,直线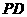 的方程:
的方程: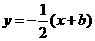 ,令
,令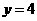 得
得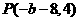 .由已知可得
.由已知可得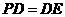 即
即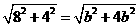 解得
解得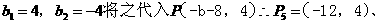
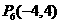 (
(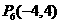 与
与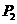 重合舍去).
重合舍去).
综上可得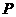 点的生标共5个解,分别为P(-12,4)、P(-4,4)、P(-
点的生标共5个解,分别为P(-12,4)、P(-4,4)、P(-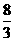 ,4)、
,4)、
P(8,4)、P(4,4).
事实上,我们可以得到更一般的结论:
如果得出
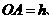 设
设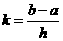 ,则P点的情形如下
,则P点的情形如下
|
直角分类情形 |
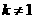 |
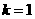 |
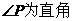 |
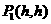 |
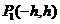 |
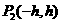 |
||
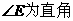 |
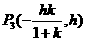 |
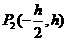 |
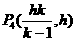 |
||
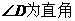 |
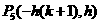 |
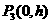 |
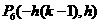 |
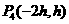 |
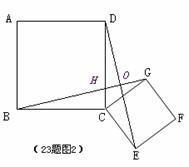
7. 解:
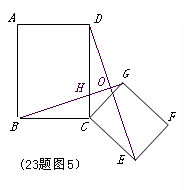
(1)①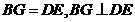 ………………………………………………………………2分
………………………………………………………………2分
② 仍然成立 ……………………………………………………1分
仍然成立 ……………………………………………………1分
在图(2)中证明如下
∵四边形 、四边形
、四边形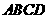 都是正方形
都是正方形
∴ 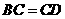 ,
,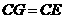 ,
, 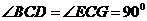
∴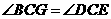 …………………………………………………………………1分
…………………………………………………………………1分
∴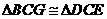 (SAS)………………………………………………………1分
(SAS)………………………………………………………1分
∴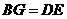
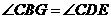
又∵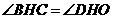
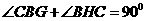
∴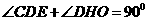 ∴
∴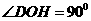
∴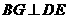 …………………………………………………………………………1分
…………………………………………………………………………1分
(2)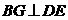 成立,
成立,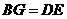 不成立 …………………………………………………2分
不成立 …………………………………………………2分
简要说明如下
∵四边形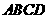 、四边形
、四边形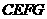 都是矩形,
都是矩形,
且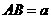 ,
,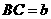 ,
,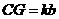 ,
,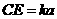 (
(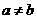 ,
,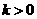 )
)
∴ 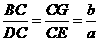 ,
,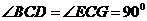
∴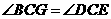
∴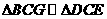 ………………………………………………………………………1分
………………………………………………………………………1分
∴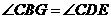
又∵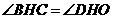
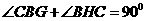
∴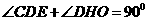 ∴
∴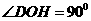
∴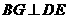 ……………………………………………………………………………1分
……………………………………………………………………………1分
(3)∵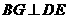 ∴
∴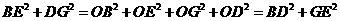
又∵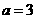 ,
,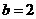 ,
,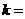
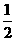
∴ 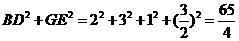 ………………………………………………1分
………………………………………………1分
∴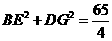 ………………………………………………………………………1分
………………………………………………………………………1分
6. 解:(1)作BE⊥OA,∴ΔAOB是等边三角形∴BE=OB·sin60o=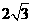 ,∴B(
,∴B(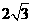 ,2)
,2)
∵A(0,4),设AB的解析式为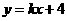 ,所以
,所以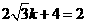 ,解得
,解得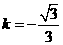 ,
,
以直线AB的解析式为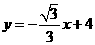
(2)由旋转知,AP=AD, ∠PAD=60o,
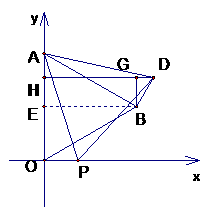 ∴ΔAPD是等边三角形,PD=PA=
∴ΔAPD是等边三角形,PD=PA=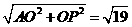
如图,作BE⊥AO,DH⊥OA,GB⊥DH,显然ΔGBD中∠GBD=30°
∴GD=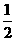 BD=
BD=
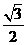 ,DH=GH+GD=
,DH=GH+GD=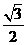 +
+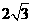 =
=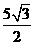 ,
,
∴GB=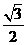 BD=
BD=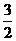 ,OH=OE+HE=OE+BG=
,OH=OE+HE=OE+BG=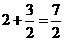
∴D(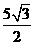 ,
,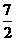 )
)
(3)设OP=x,则由(2)可得D(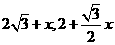 )若ΔOPD的面积为:
)若ΔOPD的面积为: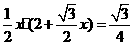
解得: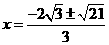 所以P(
所以P(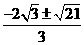 ,0)
,0)
5. 解:(1)(-4,-2);(-m,-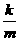 )
)
(2) ①由于双曲线是关于原点成中心对称的,所以OP=OQ,OA=OB,所以四边形APBQ一定是平行四边形
②可能是矩形,mn=k即可
不可能是正方形,因为Op不能与OA垂直.
解:(1)作BE⊥OA,
∴ΔAOB是等边三角形
∴BE=OB·sin60o=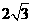 ,
,
∴B(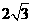 ,2)
,2)
∵A(0,4),设AB的解析式为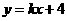 ,所以
,所以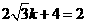 ,解得
,解得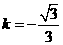 ,的以直线AB的解析式为
,的以直线AB的解析式为
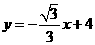
(2)由旋转知,AP=AD, ∠PAD=60o,
∴ΔAPD是等边三角形,PD=PA=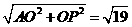
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com