
题目列表(包括答案和解析)
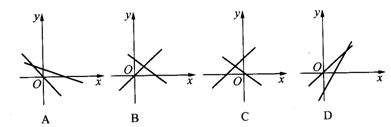
5.图8-4所示图形中,表示函数y=mx+n与正比例函数y=mnx(mn≠0)图象的是( )
4.已知直线y=ax+b经过一、二、四象限,则下列结论正确的是( )
A.a>0,b>0;B.a>0,b<0; C.a<0,b>0;D.a<0,b<0
3.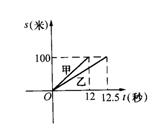 甲、乙二人在一次赛跑中,路程s与时间t的关系如图所示,从图中可以看出,下列结论错误的是( )
甲、乙二人在一次赛跑中,路程s与时间t的关系如图所示,从图中可以看出,下列结论错误的是( )
A.这是一次100米赛跑; B.甲比乙先到达终点
C.乙跑完全程需12.5秒; D.甲的速度是8米/秒
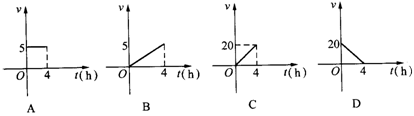
2.一根蜡烛原长20cm,点燃后每小时燃烧5cm,则燃烧的速度v(cm/h)与燃烧的时间t(h)的关系用图象表示为( )
1.如图是某市一天的气温随时间变化的图象,那么这天( )
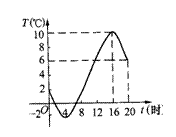 A.最高气温是10℃,最低气温是2℃;
A.最高气温是10℃,最低气温是2℃;
B.最高气温是6℃,最低气温是2℃
C.最高气温是10℃,最低气温是-2℃;
D.最高气温是6℃,最低气温是-2℃
25.现计划把甲种货物1 240吨和乙种货物880吨用一列货车运往某地,已知这列货车挂A、B两种不同规格的车厢共40节,使用A型车厢每节费用为6 000元,使用B型车厢,费用为每节8 000元.
(1)设运送这批货物的总费用为y万元,这列货车挂A型车厢x节,试写出y与x之间的函数关系式.
(2)如果每节A型车厢最多装甲种货物35吨和乙种货物15吨,每节B型车厢最多可装甲种货物25吨和乙种货物35吨,装货时按此要求安排A、B两种车厢的节数,那么共有哪几种安排车厢方案?
24.某公司到果园基地购买某种优质水果,慰问医务工作者,果园基地对购买3000千克以上(含3 000千克)的有两种销售方案.甲方案:每千克9元,由基地送货上门.乙方案:每千克8元,由顾客自己租车运回.已知该公司租车从基地到公司的运输费为5 000元.
(1)分别写出该公司的两种购买方案的付款y(元)与所购买的水果量x(千克)之间的函数关系式.
(2)当购买量在什么范围内时,选择哪种方案付款较少?说明理由.
23.如图,公园要建造圆形的喷水池,在水池中央垂直水面处安装一个柱子OA,O恰好在水面中心,OA=12.5米,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流离OA距离为1米处达到距水面最大高度2.25米,如果不计其他因素,那么水池半径至少要多少米?
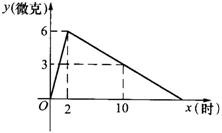
22.某医院研发了一种新药,试验药效时发现,如果成人按规定剂量服用,那么服药2小时后,血液中含药量最高,达每毫升6微克,接着逐渐衰减,10小时后血液中含药量用每毫升3微克,每毫升血液中含药y(微克)随时间x(时)的变化如图9-3所示,当成人按规定剂量服药后.
(1)分别求出x≤2和x≥2时,y与x之间的关系式.
(2)如果每毫升血液中含药量为4微克和4微克以上时治疗疾病是有效的,那么这个有效时间有多长?
21.学生甲每小时走3千米,出发1.5小时后,学生乙以每小时4.5千米的速度追赶甲,设乙行走的时间为t小时.
(1)写出甲、乙两学生走的路程s1、s2与时间t的关系式;
(2)求出直线s1与直线s2的交点坐标,并解释该坐标的实际意义.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com