
题目列表(包括答案和解析)
5、猜想变化情况
随着数字或图形的变化,它原先的一些性质有的不会改变,有的则发生了变化,而且这种变化是有一定规律的。比如,在几何图形按特定要求变化后,只要本质不变,通常的规律是“位置关系不改变,乘除乘方不改变,减变加法加变减,正号负号要互换”。这种规律可以作为猜想的一个参考依据。
例5(山东青岛)四边形是大家最熟悉的图形之一,我们已经发现了它的许多性质.只要善于观察、乐于探索,我们还会发现更多的结论.
(1)四边形一条对角线上任意一点与另外两个顶点的连线,将四边形分成四个三角形(如图7),其中相对的两对三角形的面积之积相等.你能证明这个结论吗?试试看.
已知:在四边形ABCD中,O是对角线BD上任意一点(如图7);
求证:S△OBC·S△OAD=S△OAB·S△OCD.
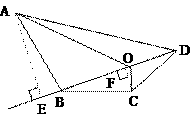
图7
(2)在三角形中(如图8),你能否归纳出类似的结论?若能,写出你猜想的结论,并证明:若不能,说明理由.
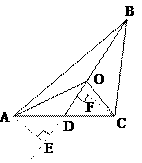
图8
分析:(1)分别过点A、C,做AE⊥DB,交DB的延长线于E,CF⊥BD于F,
则有:S△AOB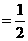 BO·AE
BO·AE
S△COD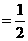 DO·CF
DO·CF
S△AOD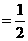 DO·AE
DO·AE
S△BOC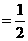 BO·CF
BO·CF
∴S△AOB ·S△COD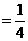 BO·DO·AE·CF
BO·DO·AE·CF
S△AOD·S△BOC 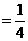 BO·DO·CF·AE
BO·DO·CF·AE
∴S△AOB ·S△COD =S△AOD·S△BOC.
(2)根据“乘除乘方不改变”能猜想到:从三角形的一个顶点与对边上任意一点的连线上任取一点,与三角形的另外两个顶点连线,将三角形分成四个小三角形,其中相对的两对三角形的面积之积相等. 或S△AOD·S△BOC=S△AOB ·S△DOC
已知:在△ABC中,D为AC上一点,O为BD上一点
求证:S△AOD·S△BOC=S△AOB ·S△DOC
证明:分别过点A、C,作AE⊥BD,交BD的延长线于E,作CF⊥BD于F,
则有:S△AOD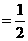 DO·AE,S△BOC
DO·AE,S△BOC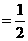 BO·CF
BO·CF
S△OAB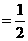 OB·AE,S△DOC
OB·AE,S△DOC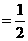 OD·CF
OD·CF
∴S△AOD·S△BOC 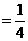 OB·OD·AE·CF
OB·OD·AE·CF
S△OAB ·S△DOC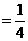 BO·OD·AE·CF
BO·OD·AE·CF
∴S△AOD·S△BOC=S△OAB ·S△DOC
4、猜想数量关系
数量关系的表现形式多种多样,这些关系不一定就是我们目前所学习的函数关系式。在猜想这种问题时,通常也是根据题目给出的关系式进行类比,仿照猜想数式规律的方法解答。
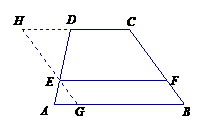 例4(江苏连云港)(1)如图5,在梯形ABCD中,AB∥CD,
例4(江苏连云港)(1)如图5,在梯形ABCD中,AB∥CD,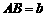 ,
,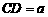 ,E为AD边上的任意一点,EF∥AB,且EF交BC于点F,某学生在研究这一问题时,发现如下事实:
,E为AD边上的任意一点,EF∥AB,且EF交BC于点F,某学生在研究这一问题时,发现如下事实:
图5
①当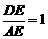 时,有
时,有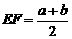 ;
;
②当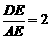 时,有
时,有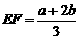 ;
;
③当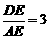 时,有
时,有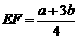 .
.
当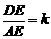 时,参照上述研究结论,请你猜想用k表示DE的一般结论,并给出证明;
时,参照上述研究结论,请你猜想用k表示DE的一般结论,并给出证明;
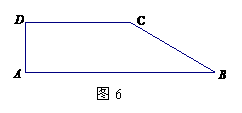 (2)现有一块直角梯形田地
(2)现有一块直角梯形田地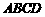 (如图6所示),其中AB∥CD,
(如图6所示),其中AB∥CD,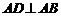 ,
,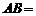 310米,
310米,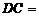 170米,
170米,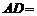 70米.若要将这块地分割成两块,由两农户来承包,要求这两块地均为直角梯形,且它们的面积相等.请你给出具体分割方案.
70米.若要将这块地分割成两块,由两农户来承包,要求这两块地均为直角梯形,且它们的面积相等.请你给出具体分割方案.
分析:猜想的东西未必完全正确,鉴于此,本题按照“猜想--证明--应用”的思路设计题目,体现了知识的产生过程、科学论证和应用价值。
(1)仿照例1、例2的解题思路,不难猜想出关系式:EF =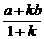 .
.
证明:过点E作BC的平行线交AB于G,交CD的延长线于H.
∵AB∥CD,∴ ∽
∽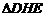 ,∴
,∴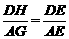 ,
,
又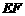 //
// //
// ,∴
,∴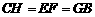 ,
,
∵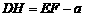 ,
,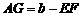 ,
,
∴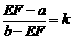 ,可得
,可得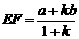 .
.
(2)在 上取一点E,作EF∥AB交BC于点F,设
上取一点E,作EF∥AB交BC于点F,设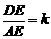 ,
,
则EF=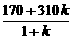 ,
,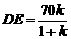 ,
,
若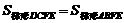 ,则
,则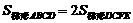 ,
,
∵梯形ABCD、DCFE为直角梯形,
∴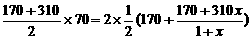
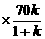 ,
,
化简得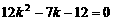 解得:
解得: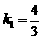 ,
,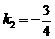 (舍去),
(舍去),
∴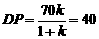 ,
,
所以只需在AD上取点E,使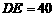 米,作EF∥AB(或
米,作EF∥AB(或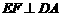 ),
),
即可将梯形分成两个直角梯形,且它们的面积相等.
2、猜想图形规律
根据一组相关图形的变化规律,从中总结通过图形的变化所反映的规律。其中,以图形为载体的数字规律最为常见。猜想这种规律,需要把图形中的有关数量关系列式表达出来,再对所列式进行对照,仿照猜想数式规律的方法得到最终结论。
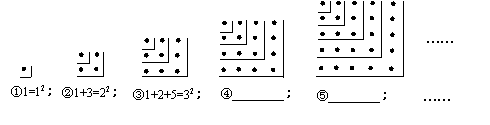 例2(河北课改实验区)观察图2所示的点阵图和相应的等式,探究其中的规律:
例2(河北课改实验区)观察图2所示的点阵图和相应的等式,探究其中的规律:
图2
(1)在④和⑤后面的横线上分别写出相应的等式;
(2)通过猜想写出与第n个点阵相对应的等式.
分析:(1)本题图形中所反映出来的数字关系已经列出三个,下面就以它们为例,填写后两个。易得④1+3+5+7=42;⑤1+3+5+7+9=52.
(2)仿照例1的思路可以猜想:1+3+5+…+(2n-1)=n2 .
1、猜想数式规律
通常给定一些数字、代数式、等式或者不等式,然后猜想其中蕴含的规律。一般解法是先写出数式的基本结构,然后通过横比(比较同一等式中不同部分的数量关系)或纵比(比较不同等式间相同位置的数量关系)找出各部分的特征,改写成要求的格式。
例1(云南)观察按下列顺序排列的等式:
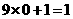 ;
;
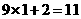 ;
;
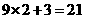 ;
;
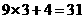 ;
;
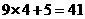 ;
;
……
猜想:第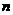 个等式(
个等式(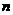 为正整数)用
为正整数)用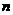 表示,可以表示成________________.
表示,可以表示成________________.
分析:根据以上各等式所呈现出来的特征,可以猜想这个等式的基本结构形式为
9 × 一个数 + 另一个数 = 结果
其中,“另一个数”就是等式的序号n;“一个数”比它小1,即为n-1;结果的个位为1,个位以前的数字等于“一个数”n-1,所以结果表示为10(n-1)+1. 因此,这个等式为
9(n-1) + n = 10(n-1) + 1.
这个猜想的结果是否正确,还可以用整式运算的知识加以验证。
等式的左边 = 9n - 9 + n = 10n – 9;等式的右边 = 10n – 10 + 1 = 10n – 9 .
所以,等式的左边 = 等式的右边。
说明所列等式成立。
猜想规律型的问题难度相对较小,经常以填空等形式出现,解题时要善于从所提供的数字或图形信息中,寻找其共同之处,这个存在于个例中的共性,就是规律。其中蕴含着“特殊--一般--特殊”的常用模式,体现了总结归纳的数学思想,这也正是人类认识新生事物的一般过程。
相对而言,猜想结论型问题的难度较大些,具体题目往往是直观猜想与科学论证、具体应用的结合,解题的方法也更为灵活多样:计算、验证、类比、比较、测量、绘图、移动等等,都能用到。
由于猜想本身就是一种重要的数学方法,也是人们探索发现新知的重要手段,非常有利于培养创造性思维能力,所以备受命题专家的青睐,逐步成为中考的又一热点。
如图1所示:

图1
能够根据题目中的图形或者数字直观地发现共同特征,或者发展变化的趋势,据此去预测估计它的规律或者其他相关结论,使带有猜想性质的推断尽可能与现实情况相吻合,必要时可以进行验证或者证明,依此体现出猜想的实际意义。
2、如图6,在平面直角坐标系内,Rt△ABC的直角顶点C(0,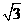 )在
)在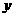 轴的正半轴上,A、B是
轴的正半轴上,A、B是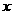 轴上是两点,且OA∶OB=3∶1,以OA、OB为直径的圆分别交AC于点E,交BC于点F.直线EF交OC于点Q.
轴上是两点,且OA∶OB=3∶1,以OA、OB为直径的圆分别交AC于点E,交BC于点F.直线EF交OC于点Q.
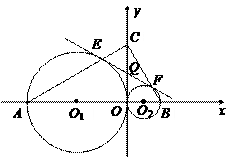
图6
求过A、B、C三点的抛物线的解析式;
请猜想:直线EF与两圆有怎样的位置关系?并证明你的猜想.
在△AOC中,设点M是AC边上的一个动点,过M作MN∥AB交OC于点N.试问:在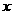 轴上是否存在点P,使得△PMN是一个以MN为一直角边的等腰直角三角形?若存在,求出P点坐标;若不存在,请说明理由.
轴上是否存在点P,使得△PMN是一个以MN为一直角边的等腰直角三角形?若存在,求出P点坐标;若不存在,请说明理由.
1、如图5-1,边长为2的正方形ABCD中,顶点A的坐标是(0,2),一次函数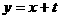 的图象
的图象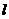 随
随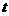 的不同取值变化时,位于
的不同取值变化时,位于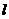 的右下方由
的右下方由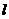 和正方形的边围成的图形面积为
和正方形的边围成的图形面积为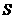 (阴影部分).
(阴影部分).
⑴当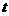 何值时,
何值时,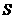 =3?
=3?
⑵在平面直角坐标系下(图5-2),画出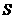 与
与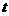 的函数图象.
的函数图象.
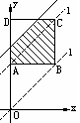

图5-1 图5-2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com