
题目列表(包括答案和解析)
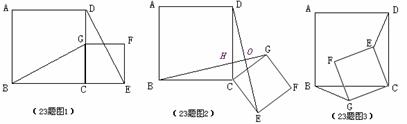
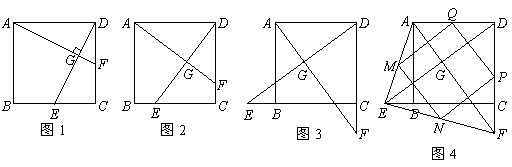
18、(义乌市08)如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系:
(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系;
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度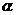 ,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
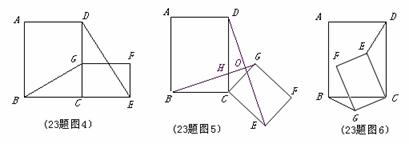 (2)将原题中正方形改为矩形(如图4-6),且AB=a,BC=b,CE=ka, CG=kb (a
(2)将原题中正方形改为矩形(如图4-6),且AB=a,BC=b,CE=ka, CG=kb (a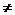 b,k
b,k 0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.
0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.
17、如图,先把一张矩形纸片ABCD对折,折痕为MN,再把B点叠在折痕线上,得到△ABE,过点B折纸片使点D叠在直线AD上,得折痕为PQ.
(1)求证:△PBE∽△QAB.
(1)你认为△PBE和△BAE相似吗?如果相似,给出证明。如果不相似,请说明理由。
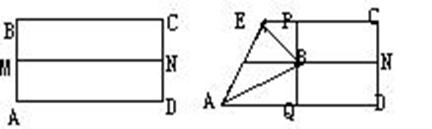 (2)若沿直线EB折叠纸片,则点A是否能叠在直线EC上?为什么?
(2)若沿直线EB折叠纸片,则点A是否能叠在直线EC上?为什么?
16、(咸宁市08)如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
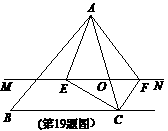 (1)求证:EO=FO;
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?
并证明你的结论.
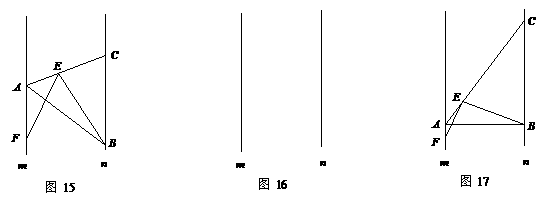
(08大连)点A、B分别是两条平行线m、n上任意两点,在直线n上找一点C,使BC = kAB,连结AC,在直线AC上任取一点E,作∠BEF =∠ABC,EF交直线m于点F.
⑴如图15,当k = 1时,探究线段EF与EB的关系,并中以说明;
说明:①如果你经过反复探索没有解决问题,请写出探索过程(要求至少写三步);
②在完成①之后,可以自己添加条件(添加的条件限定为∠ABC为特殊角),在图16中补全图形,完成证明(选择添加条件比原题少得3分).
⑵如图17,若∠ABC = 90°,k≠1,探究线段EF与EB的关系,并说明理由.
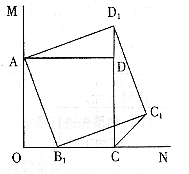
15、(眉山市06)如图:∠MON = 90°,在∠MON的内部有一个正方形AOCD,点A、C分别在射线OM、ON上,点B1是ON上的任意一点,在∠MON的内部作正方形AB1C1D1。
(1)连续D1D,求证:∠ADD1 = 90°;
(2)连结CC1,猜一猜,∠C1CN的度数是多少?并证明你的结论;
(3)在ON上再任取一点B2,以AB2为边,在∠MON的内部作正方形AB2C2D2,观察图形,并结合(1)、(2)的结论,请你再做出一个合理的判断。
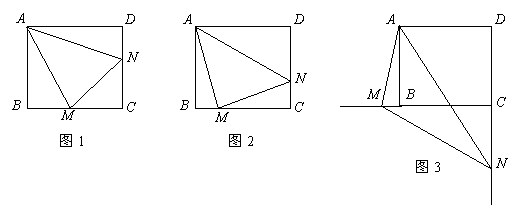
14、(08齐齐哈尔)已知:正方形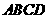 中,
中,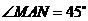 ,
,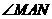 绕点
绕点 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交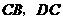 (或它们的延长线)于点
(或它们的延长线)于点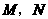 .
.
当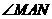 绕点
绕点 旋转到
旋转到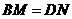 时(如图1),易证
时(如图1),易证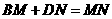 .
.
(1)当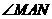 绕点
绕点 旋转到
旋转到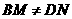 时(如图2),线段
时(如图2),线段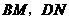 和
和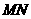 之间有怎样的数量关系?写出猜想,并加以证明.
之间有怎样的数量关系?写出猜想,并加以证明.
 (2)当
(2)当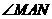 绕点
绕点 旋转到如图3的位置时,线段
旋转到如图3的位置时,线段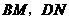 和
和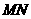 之间又有怎样的数量关系?请直接写出你的猜想.
之间又有怎样的数量关系?请直接写出你的猜想.
13、(07资阳)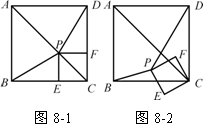 如图8-1,已知P为正方形ABCD的对角线AC上一点(不与A、C重合),PE⊥BC于点E,PF⊥CD于点F.
如图8-1,已知P为正方形ABCD的对角线AC上一点(不与A、C重合),PE⊥BC于点E,PF⊥CD于点F.
(1) 求证:BP=DP;
(2) 如图8-2,若四边形PECF绕点C按逆时针方向旋转,在旋转过程中是否总有BP=DP?若是,请给予证明;若不是,请用反例加以说明;
(3) 试选取正方形ABCD的两个顶点,分别与四边形PECF的两个顶点连结,使得到的两条线段在四边形PECF绕点C按逆时针方向旋转的过程中长度始终相等,并证明你的结论 .
12、(06 沈阳)如图1,在正方形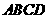 中,点
中,点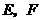 分别为边
分别为边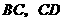 的中点,
的中点,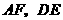 相交于点
相交于点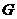 ,则可得结论:①
,则可得结论:①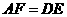 ;②
;②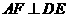 .(不需要证明)
.(不需要证明)
(1)如图2,若点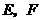 不是正方形
不是正方形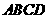 的边
的边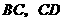 的中点,但满足
的中点,但满足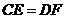 ,则上面的结论①,②是否仍然成立?(请直接回答“成立”或“不成立”)
,则上面的结论①,②是否仍然成立?(请直接回答“成立”或“不成立”)
(2)如图3,若点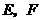 分别在正方形
分别在正方形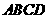 的边
的边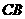 的延长线和
的延长线和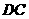 的延长线上,且
的延长线上,且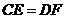 ,此时上面的结论1,2是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由.
,此时上面的结论1,2是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由.
(3)如图4,在(2)的基础上,连接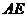 和
和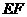 ,若点
,若点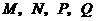 分别为
分别为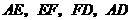 的中点,请判断四边形
的中点,请判断四边形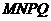 是“矩形、菱形、正方形、等腰梯形”中的哪一种?并写出证明过程.
是“矩形、菱形、正方形、等腰梯形”中的哪一种?并写出证明过程.
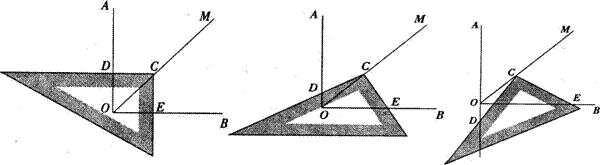
11、(06年鸡西)已知∠AOB=900,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA、OB(或它们的反向延长线)相交于点D、E.
当三角板绕点C旋转到CD与OA垂直时(如图1),易证:OD+OE=OC.
当三角板绕点C旋转到CD与OA不垂直时,在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段OD、OE、OC之间又有怎样的数量关系?请写出你的猜想,不需证明。
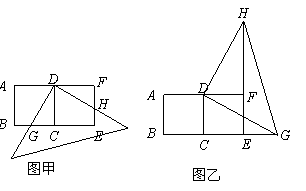
(08枣庄)把一副三角板如图甲放置,其中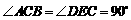 ,
,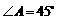 ,
,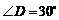 ,斜边
,斜边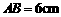 ,
,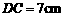 .把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点
.把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点 ,与D1E1相交于点F.
,与D1E1相交于点F.
(1)求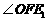 的度数;
的度数;
(2)求线段AD1的长;
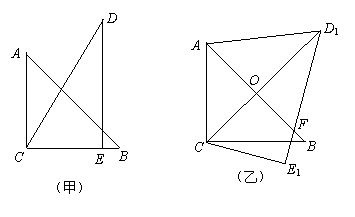 (3)若把三角形D1CE1绕着点
(3)若把三角形D1CE1绕着点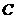 顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?说明理由.
顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?说明理由.
10、(2006 梅州)用两个全等的正方形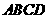 和
和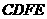 拼成一个矩形
拼成一个矩形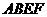 ,把一个足够大的直角三角尺的直角顶点与这个矩形的边
,把一个足够大的直角三角尺的直角顶点与这个矩形的边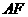 的中点
的中点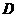 重合,且将直角三角尺绕点
重合,且将直角三角尺绕点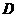 按逆时针方向旋转.
按逆时针方向旋转.
(1)当直角三角尺的两直角边分别与矩形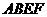 的两边
的两边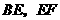 相交于点
相交于点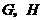 时,如图甲,通过观察或测量
时,如图甲,通过观察或测量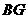 与
与 的长度,你能得到什么结论?并证明你的结论.
的长度,你能得到什么结论?并证明你的结论.
(2)当直角三角尺的两直角边分别与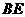 的延长线,
的延长线,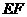 的延长线相交于点
的延长线相交于点 时(如图乙),你在图甲中得到的结论还成立吗?简要说明理由.
时(如图乙),你在图甲中得到的结论还成立吗?简要说明理由.
9、(台州08) 经过
经过 顶点
顶点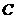 的一条直线,
的一条直线,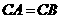 .
.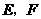 分别是直线
分别是直线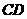 上两点,且
上两点,且 .
.
(1)若直线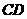 经过
经过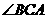 的内部,且
的内部,且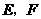 在射线
在射线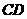 上,请解决下面两个问题:
上,请解决下面两个问题:
①如图1,若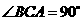 ,
,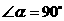 ,
,
则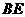
 ;
;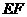
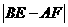 (填“
(填“ ”,“
”,“ ”或“
”或“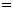 ”);
”);
②如图2,若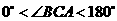 ,请添加一个关于
,请添加一个关于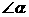 与
与 关系的条件
,使①中的两个结论仍然成立,并证明两个结论成立.
关系的条件
,使①中的两个结论仍然成立,并证明两个结论成立.
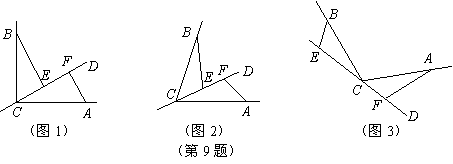 (2)如图3,若直线
(2)如图3,若直线 经过
经过 的外部,
的外部,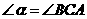 ,请提出
,请提出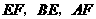 三条线段数量关系的合理猜想(不要求证明).
三条线段数量关系的合理猜想(不要求证明).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com