
题目列表(包括答案和解析)
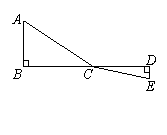
10、如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC已知AB=5,DE=1,BD=8,设CD=x.
(1)用含x的代数式表示AC+CE的长;
(2)请问点C满足什么条件时,AC+CE的值最小?
(3)根据(2)中的规律和结论,请构图求出代数式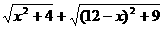 的最小值.
的最小值.
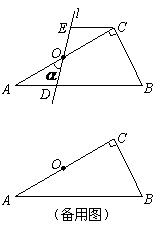
9、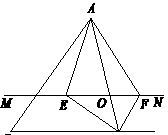 如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?
并证明你的结论.
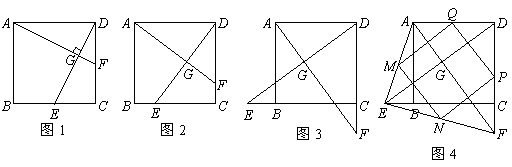
8、如图1,在正方形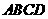 中,点
中,点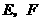 分别为边
分别为边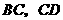 的中点,
的中点,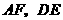 相交于点
相交于点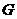 ,则可得结论:①
,则可得结论:①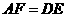 ;②
;②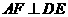 .(不需要证明)
.(不需要证明)
(1)如图2,若点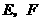 不是正方形
不是正方形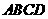 的边
的边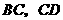 的中点,但满足
的中点,但满足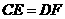 ,则上面的结论①,②是否仍然成立?(请直接回答“成立”或“不成立”)
,则上面的结论①,②是否仍然成立?(请直接回答“成立”或“不成立”)
(2)如图3,若点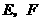 分别在正方形
分别在正方形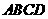 的边
的边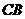 的延长线和
的延长线和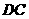 的延长线上,且
的延长线上,且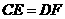 ,此时上面的结论1,2是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由.
,此时上面的结论1,2是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由.
(3)如图4,在(2)的基础上,连接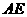 和
和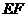 ,若点
,若点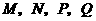 分别为
分别为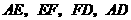 的中点,请判断四边形
的中点,请判断四边形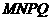 是“矩形、菱形、正方形、等腰梯形”中的哪一种?并写出证明过程.
是“矩形、菱形、正方形、等腰梯形”中的哪一种?并写出证明过程.
7、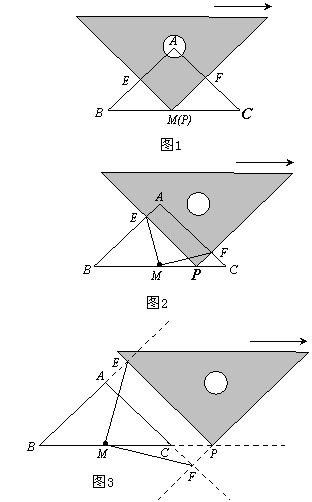 在△ABC中,AB=AC,AC⊥BA,M为BC边中点,一等腰直角三角尺的直角顶点P在BC边上移动,两直角边分别与AB,AC交于E,F两点且斜边与BC平行.
在△ABC中,AB=AC,AC⊥BA,M为BC边中点,一等腰直角三角尺的直角顶点P在BC边上移动,两直角边分别与AB,AC交于E,F两点且斜边与BC平行.
(1)在图1中,当三角尺的直角顶点P恰好移动到M点时,请你通过观察、测量,猜想并写出ME与M F满足的数量关系及位置关系,然后证明你的猜想;
(2)当三角尺的直角顶点P沿BC方向移动到图2所示的位置时,请你通过观察、测量、猜想并写出ME与MF满足的数量关系及位置关系,然后证明你的猜想;
(3)当三角尺在(2)的基础上沿BC方向继续向右平移到图3所示的位置(点P在线段BC的延长线上,三角尺两直角边所在直线与△ABC的两边BA,AC的延长线分别交于点E,F,且点P与点C不重合)时,(2)中的猜想是否仍然成立?(不用说明理由)
6、如图,在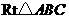 中,
中,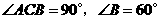 ,
,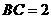 .点
.点 是
是 的中点,过点
的中点,过点 的直线
的直线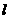 从与
从与 重合的位置开始,绕点
重合的位置开始,绕点 作逆时针旋转,交
作逆时针旋转,交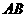 边于点
边于点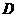 .过点
.过点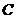 作
作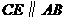 交直线
交直线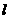 于点
于点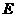 ,设直线
,设直线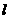 的旋转角为
的旋转角为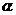 .
.
(1)①当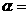 度时,四边形
度时,四边形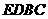 是等腰梯形,此时
是等腰梯形,此时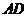 的长为 ;
的长为 ;
②当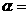 度时,四边形
度时,四边形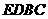 是直角梯形,此时
是直角梯形,此时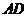 的长为 ;
的长为 ;
(2)当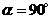 时,判断四边形
时,判断四边形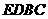 是否为菱形,并说明理由.
是否为菱形,并说明理由.
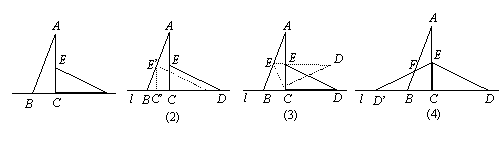
5、将两块全等的含30°角的三角尺如图(1)摆放在一起,它们的较短直角边长为3.(1) 将△ECD沿直线l向左平移到图(2)的位置,使E点落在AB上,则CC′=______;
(2) 将△ECD绕点C逆时针旋转到图(3)的位置,使点E落在AB上,则△ECD绕点C旋转的度数=______;
(3) 将△ECD沿直线AC翻折到图(4)的位置,ED′与AB相交于点F,求证AF=FD′
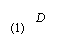
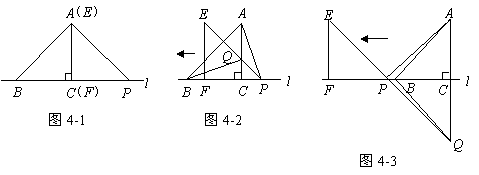
4、如图4-1, 的边
的边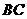 在直线
在直线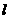 上,
上,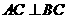 ,且
,且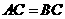 ;
;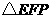 的边
的边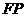 也在直线
也在直线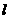 上,边
上,边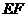 与边
与边 重合,且
重合,且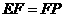 .
.
(1)在图4-1中,请你通过观察、测量,猜想并写出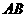 与
与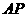 所满足的数量关系和位置关系;
所满足的数量关系和位置关系;
(2)将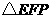 沿直线
沿直线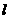 向左平移到图4-2的位置时,
向左平移到图4-2的位置时,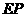 交
交 于点
于点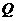 ,连结
,连结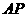 ,
,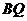 .猜想并写出
.猜想并写出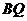 与
与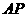 所满足的数量关系和位置关系,请证明你的猜想;
所满足的数量关系和位置关系,请证明你的猜想;
(3)将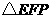 沿直线
沿直线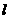 向左平移到图4-3的位置时,
向左平移到图4-3的位置时,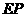 的延长线交
的延长线交 的延长线于点
的延长线于点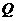 ,连结
,连结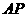 ,
,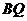 .你认为(2)中所猜想的
.你认为(2)中所猜想的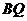 与
与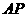 的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.
的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.

1、用两个全等的正方形 和
和 拼成一个矩
拼成一个矩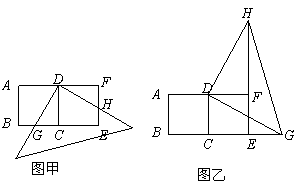 形
形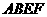 ,把一个足够大的直角三角尺的直角顶点与这个矩形的边
,把一个足够大的直角三角尺的直角顶点与这个矩形的边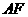 的中点
的中点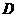 重合,且将直角三角尺绕点
重合,且将直角三角尺绕点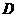 按逆时针方向旋转.
按逆时针方向旋转.
(1)当直角三角尺的两直角边分别与矩形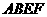 的两边
的两边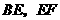 相交于点
相交于点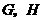 时,如图甲,通过观察或测量
时,如图甲,通过观察或测量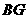 与
与 的长度,你能得到什么结论?并证明你的结论.
的长度,你能得到什么结论?并证明你的结论.
(2)当直角三角尺的两直角边分别与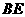 的延长线,
的延长线,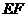 的延长线相交于点
的延长线相交于点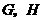 时(如图乙),你在图甲中得到的结论还成立吗?简要说明理由.
时(如图乙),你在图甲中得到的结论还成立吗?简要说明理由.

7.解:(1)设高级教师招聘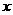 人,则中级教师招聘
人,则中级教师招聘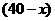 人
人
依题意得: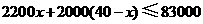
解此不等式得: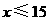
又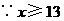
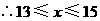
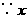 是正整数,
是正整数,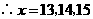
 学校对高级教师,中级教师有三种招聘方案
学校对高级教师,中级教师有三种招聘方案

(2)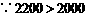 ,即高级教师的月薪大于中级教师的月薪.
,即高级教师的月薪大于中级教师的月薪.
 高级教师的招聘人数越小,学校所支付的月工资越少.
高级教师的招聘人数越小,学校所支付的月工资越少.
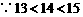
 当高级教师招聘13人,中级教师招聘27人时,学校所支付的月工资最少.
当高级教师招聘13人,中级教师招聘27人时,学校所支付的月工资最少.
(3)补表:13、27
在学校所支付的月工资最少时,中位数是2100元,众数是2000元
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com