
题目列表(包括答案和解析)
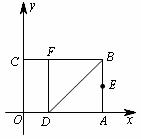
8.(·福州市)如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
(1)直接写出点E、F的坐标;
(2)设顶点为F的抛物线交y轴正半轴于点P,且以点E、F、P为顶点的三角形是等腰三角形,求该抛物线的解析式;
(3)在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.
第8课时 分类讨论题 答案
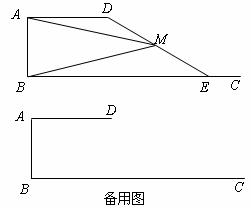
7.(·上海市)已知AB=2,AD=4,∠DAB=90°,AD∥BC(如图).E是射线BC上的动点(点E与点B不重合),M是线段DE的中点.
(1)设BE=x,△ABM的面积为y,求y关于x的函数解析式,并写出函数的定义域;
(2)如果以线段AB为直径的圆与以线段DE为直径的圆外切,求线段BE的长;
(3)联结BD,交线段AM于点N,如果以A、N、D为顶点的三角形与△BME相似,求线段BE的长.












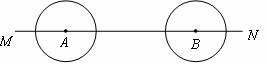
6.(•威海市)如图,点A,B在直线MN上,AB=11厘米,⊙A,⊙B的半径均为1厘米.⊙A以每秒2厘米的速度自左向右运动,与此同时,⊙B的半径也不断增大,其半径r(厘米)与时间t(秒)之间的关系式为r=1+t(t≥0). 
(1)试写出点A,B之间的距离d(厘米)与时间t(秒)之间的函数表达式; 
(2)问点A出发后多少秒两圆相切? 






类型之三 方程、函数中的分类讨论
方程、函数的分类讨论主要是通过变量之间的关系建立函数关系式,然后根据实际情况进行分类讨论或在有实际意义的情况下的讨论,在讨论问题的时候要注意特殊点的情况.
5.(上海市)在△ABC中,AB=AC=5,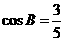 .如果圆O的半径为
.如果圆O的半径为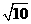 ,且经过点B、C,那么线段AO的长等于
.
,且经过点B、C,那么线段AO的长等于
.

4.(•湖北罗田)在Rt△ABC中,∠C=900,AC=3,BC=4.若以C点为圆心, r为半径 所作的圆与斜边AB只有一个公共点,则r的取值范围是___ __.
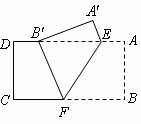
3. (·江西省)如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,(1)求证:B′E=BF;(2)设AE=a,AB=b, BF=c,试猜想a、b、c之间有何等量关系,并给予证明.











类型之二 圆中的分类讨论
圆既是轴对称图形,又是中心对称图形,在解决圆的有关问题时,特别是无图的情况下,有时会以偏盖全、造成漏解,其主要原因是对问题思考不周、思维定势、忽视了分类讨论等.
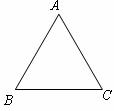
2.(•乌鲁木齐)某等腰三角形的两条边长分别为3cm和6cm,则它的周长为( )
A.9cm B.12cm C.15cm D.12cm或15cm
1.(·沈阳市)若等腰三角形中有一个角等于50°,则这个等腰三角形的顶角的度数为( )
A.50° B.80° C.65°或50° D.50°或80°
8.[解析]这是一道坐标几何题,中考中的坐标几何题,融丰富的几何图象于一题,包含的知识点较多;代数变换(包括数式变换、方程变换、不等式变换)与几何推理巧妙融合,交相辉映,数形结合思想和方法得到充分运用.本题(2)中的面积的计算是根据旋转不变性,构造全等三角形,将四边形的面积进行转化,这是一种重要的数学思想方法.
[答案]:证明:(1)3.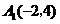 ,
,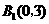
(2)作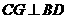 于
于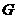 ,
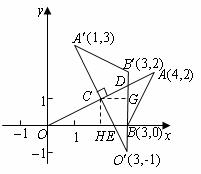
,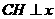 轴于
轴于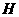 ,
,
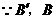 的横坐标相等,
的横坐标相等,
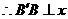 轴,
轴, 四边形
四边形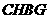 为矩形.
为矩形.
又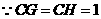 ,
, 矩形
矩形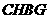 为正方形.
为正方形.
 .
.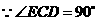 ,
,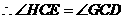 .
.
在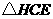 和
和 中,
中,
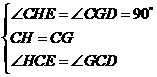
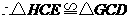 .
.
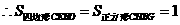 .
.
(3)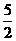 .
.
7.[解析]解决运动型的问题,关键是将其运用过程在头脑当中预演一遍,找准其运用时各个量的变化规律,再动中取静,得到相关量之间的关系.
[答案]解:(1)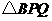 是等边三角形.
是等边三角形.
当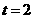 时.
时.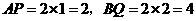 .
.
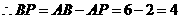 .
.
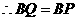 .
.
又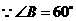 ,
,
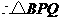 是等边三角形.
是等边三角形.
(2)过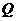 作
作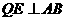 ,垂足为
,垂足为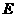 .
.
由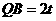 ,得
,得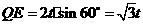 .
.
由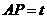 ,得
,得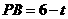 .
.
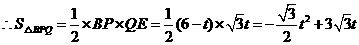 .
.
(3)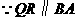 ,
,
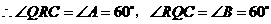 .
.
又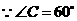 ,
, 是等边三角形.
是等边三角形.
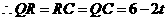 .
.
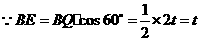 ,
,
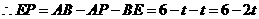 ,
,
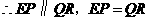 .
.
 四边形
四边形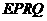 是平行四边形.
是平行四边形.
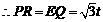 .
.
又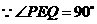 ,
,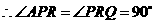 .
.
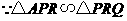 ,
,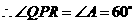 .
.
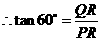 ,即
,即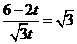 .
.
解得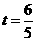 .
.
 当
当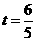 时,
时,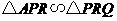
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com