
题目列表(包括答案和解析)
24、(08孝感)锐角 中,
中,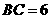 ,
,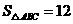 ,两动点
,两动点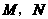 分别在边
分别在边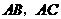 上滑动,且
上滑动,且 ,以
,以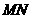 为边向下作正方形
为边向下作正方形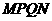 ,设其边长为
,设其边长为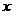 ,正方形
,正方形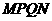 与
与 公共部分的面积为
公共部分的面积为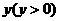 .
.
(1) 中边
中边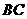 上高
上高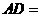 ;
;
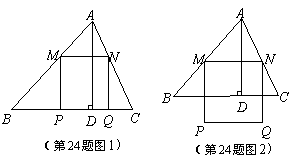 (2)当
(2)当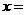 时,
时,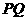 恰好落在边
恰好落在边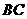 上(如图1);
上(如图1);
(3)当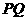 在
在 外部时(如图2),求y关于x的
外部时(如图2),求y关于x的
函数关系式(注明x的取值范围),并求出x为何值时
y最大,最大值是多少?
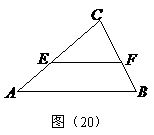
23、(07年南宁)如图,在锐角 中,
中,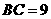 ,
,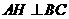 于点
于点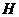 ,且
,且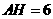 ,点
,点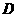 为
为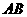 边上的任意一点,过点
边上的任意一点,过点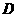 作
作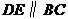 ,交
,交 于点
于点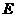 .设
.设 的高
的高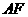 为
为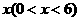 ,以
,以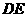 为折线将
为折线将 翻折,所得的
翻折,所得的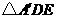 与梯形
与梯形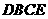 重叠部分的面积记为
重叠部分的面积记为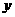 (点
(点 关于
关于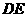 的对称点
的对称点 落在
落在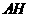 所在的直线上).
所在的直线上).
(1)分别求出当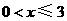 与
与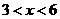 时,
时,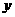 与
与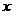 的函数关系式;
的函数关系式;
(2)当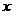 取何值时,
取何值时,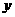 的值最大?最大值是多少?
的值最大?最大值是多少?

22、(06锦州)如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方).
(1)求A、B两点的坐标;
(2)设△OMN的面积为S,直线l运动时间为t秒(0≤t≤6),试求S与t的函数表达式;
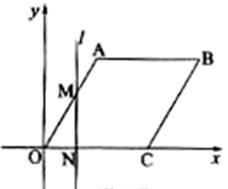 (3)在题(2)的条件下,t为何值时,S的面积最大?
(3)在题(2)的条件下,t为何值时,S的面积最大?
最大面积是多少?
21、(07吉林)如图①,在边长为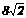 cm的正方形ABCD中,E、F是对角线AC上的两个
cm的正方形ABCD中,E、F是对角线AC上的两个
动点,它们分别从点A、点C同时出发,沿对角线以1cm/s的相同速度运动,过E作EH垂
直AC交Rt△ACD的直角边于H;过F作FG垂直AC交Rt△ACD的直角边于G,连接HG、
EB.设HE、EF、FG、GH围成的图形面积为S1,AE、EB、BA围成的图形面积为S2(这里
规定:线段的面积为0).E到达C,F到达A停止.若E的运动时间为xs,解答下列问题:
(1)当0<x<8时,直接写出以E、F、G、H为顶点的四边形是什么四边形,并求出x为何值时,S1=S2;
(2)①若y是S1与S2的和,求y与x之间的函数关系式; (图②为备用图)
②求y的最大值.

20、(内江07)在 中,
中,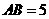 ,
, ,
,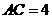 ,动点
,动点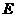 (与点
(与点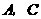 不重合)在
不重合)在 边上,
边上,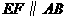 交
交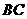 于
于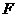 点.
点.
(1)当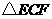 的面积与四边形
的面积与四边形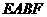 的面积相等时,求
的面积相等时,求 的长;
的长;
(2)当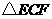 的周长与四边形
的周长与四边形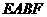 的周长相等时,求
的周长相等时,求 的长;
的长;
(3)试问在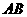 上是否存在点
上是否存在点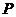 ,使得
,使得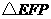 为等腰直角三角形?若不存在,请简要理由;若存在,请求出
为等腰直角三角形?若不存在,请简要理由;若存在,请求出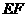 的长.
的长.

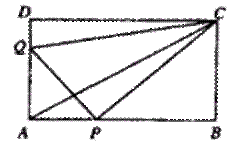
19、(02河北)如图,在矩形ABCD中,AB=12厘米,BC=6厘米,点P沿AB边从点A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D开始向点A以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么:
(1)当t为何值时,△QAP为等腰直角三角形?
(2)求四边形QAPC的面积;提出一个与计算结果有关的结论;
(3)当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似?
17、(06临沂)如图,在矩形ABCD中,AB=3cm,BC=4cm。设P、Q分别为BD、BC上的动点,在点P自点D沿DB方向作匀速移动的同时,点Q自点B沿BC方向向点C作匀速移动,移动的速度均为1cm/s,设P、Q移动的时间为t(0<t≤4)。
(1)当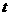 为何值时,PQ⊥BC?
为何值时,PQ⊥BC?
(2)写出△PBQ的面积S(cm2)与时间t(s)之间的函数表达式,当t为何值时,S有最大值?最大值是多少?
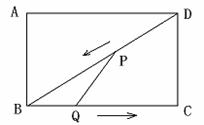 (3)是否存在某一时刻,使PQ平分△BDC的面积.
(3)是否存在某一时刻,使PQ平分△BDC的面积.
(4)△PBQ能否成为等腰三角形?若能,求t的值;若不能,说明理由。
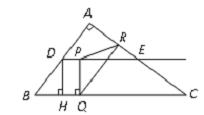 (08温州)如图,在Rt△ABC中,∠A=90º,AB=6,AC=8,D,E分别是边AB,AC的中点,点P从点D出发沿DE方向运动,过点P作PQ⊥BC于Q,过点Q作QR∥BA交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,QR=y.(1)求点D到BC的距离DH的长;(2)求y关于x的函数关系式(不要求写出自变量的取值范围);(3)是否存在点P,使△PQR为等腰三角形?若存在,请求出所有满足要求的x的值;若不存在,请说明理由.
(08温州)如图,在Rt△ABC中,∠A=90º,AB=6,AC=8,D,E分别是边AB,AC的中点,点P从点D出发沿DE方向运动,过点P作PQ⊥BC于Q,过点Q作QR∥BA交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,QR=y.(1)求点D到BC的距离DH的长;(2)求y关于x的函数关系式(不要求写出自变量的取值范围);(3)是否存在点P,使△PQR为等腰三角形?若存在,请求出所有满足要求的x的值;若不存在,请说明理由.
如图13,已知在矩形ABCD中,AD=8,CD=4,点E从点D出发,沿线段DA以每秒1个单位长的速度向点A方向移动,同时点F从点C出发,沿射线CD方向以每秒2个单位长的速度移动,当B,E,F三点共线时,两点同时停止运动.设点E移动的时间为t(秒).
(1)求当t为何值时,两点同时停止运动;
(2)设四边形BCFE的面积为S,求S与t之间的函数关系式,并写出t的取值范围;
(3)求当t为何值时,以E,F,C三点为顶点的三角形是等腰三角形;
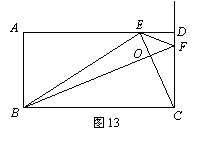 (4)求当t为何值时,∠BEC=∠BFC.
(4)求当t为何值时,∠BEC=∠BFC.
16、(07河池)如图, 四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4). 点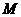 从
从 出发以每秒2个单位长度的速度向
出发以每秒2个单位长度的速度向 运动;点
运动;点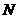 从
从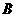 同时出发,以每秒1个单位长度的速度向
同时出发,以每秒1个单位长度的速度向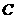 运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点
运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点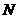 作
作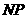 垂直
垂直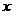 轴于点
轴于点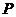 ,连结AC交NP于Q,连结MQ.
,连结AC交NP于Q,连结MQ.
(1)点 (填M或N)能到达终点;
(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;
 (3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标,若不存在,说明理由.
(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标,若不存在,说明理由.


15、已知:如图,Rt△ABC中,∠C=90°,AC=6,BC=12.点P从点A出发沿AC向点C以每秒1个单位长度的速度移动,点Q从点C出发沿CB向点B以每秒1个单位长度的速度移动,点P、Q同时出发,设移动的时间为t秒(t>0).
⑴设△PCQ的面积为y, 求y关于t的函数关系式;
⑵设点C关于直线PQ的对称点为D,问:t为何值时四边形PCQD是正方形?
⑶当得到正方形PCQD后,点P不再移动,但正方形PCQD继续沿CB边向B点以每秒1个单位长度的速度移动,当点Q与点B重合时,停止移动.设运动中的正方形为MNQD,正方形MNQD与Rt△ABC重合部分的面积为S,求:
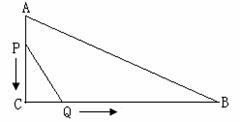 ①当3≤t≤6时,S关于t的函数关系式;
①当3≤t≤6时,S关于t的函数关系式;
②当6<t≤9时,S关于t的函数关系式;
③当9<t≤12时,S关于t的函数关系式.
(08苏州)如图,在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12.动点P从D点出发沿DC以每秒1个单位的速度向终点C运动,动点Q从C点出发沿CB以每秒2个单位的速度向B点运动.两点同时出发,当P点到达C点时,Q点随之停止运动.
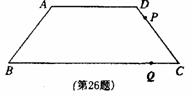 (1)梯形ABCD的面积等于 ;
(1)梯形ABCD的面积等于 ;
(2)当PQ//AB时,P点离开D点的时间等于
秒;
(3)当P、Q、C三点构成直角三角形时,P点离开
D点多少时间?
14、(05河北)如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21. 动点P从点D出发,沿射线DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动. 点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动. 设运动的时间为t(秒).
(1)设△B P Q的面积为S,求S与t之间的函数关系式;
(2)当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?
(3)当线段PQ与线段AB相交于点O,且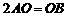 时,求∠BQP的正切值;
时,求∠BQP的正切值;
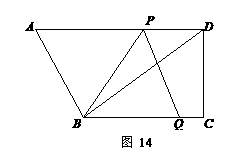 (4)是否存在时刻t,使得PQ⊥BD?若存在,求出t的值;若不存在,请说明理由.
(4)是否存在时刻t,使得PQ⊥BD?若存在,求出t的值;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com