
题目列表(包括答案和解析)
21、(08凉山)我州有一种可食用的野生菌,上市时,外商李经理按市场价格20元/千克收购了这种野生菌1000千克存放入冷库中,据预测,该野生菌的市场价格将以每天每千克上涨1元;但冷冻存放这批野生菌时每天需要支出各种费用合计310元,而且这类野生菌在冷库中最多保存160天,同时,平均每天有3千克的野生菌损坏不能出售.
(1)设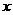 天后每千克该野生菌的市场价格为
天后每千克该野生菌的市场价格为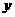 元,试写出
元,试写出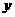 与
与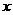 之间的函数关系式.
之间的函数关系式.
(2)若存放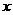 天后,将这批野生菌一次性出售,设这批野生菌的销售总额为
天后,将这批野生菌一次性出售,设这批野生菌的销售总额为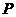 元,试写出
元,试写出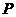 与
与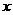 之间的函数关系式.
之间的函数关系式.
(3)李经理将这批野生菌存放多少天后出售可获得最大利润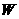 元?
元?
(利润=销售总额-收购成本-各种费用)
20、(河北02)某商店经销一种销售成本为每千克40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨1元,月销售量就减少10千克.针对这种水产品的销售情况,请售答以下问题:
(1)当销售单价定为每千克55元时,计算月销售量和月销售利润;
(2)设销售单价为每千克x元,月销售利润为y元,求y与x函数关系式(不必写出x的取值范围);
(3)商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
19、(天门07)某瓜果基地市场部为指导该基地某种蔬菜的生产销售,在对历年市场行情和生产情况进行调查的基础上,对今年这种蔬菜上市后的市场售价和生产成本进行了预测,提供了两个方面的信息,如图所示。注:两图中的每个实心点所对应的纵坐标分别指相应月份的售价和成本,生产成本6月份最低,图甲的图像是线段,图乙的图像是抛物线。
请你根据图像提供的信息说明:
(1)在3月份出售这种蔬菜,每千克的收益是多少元?(收益=售价-成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?说明理由;
(3)已知市场部销售该种蔬菜,4、5两个月的总收益为48万元,且5月份的销量比4月份的销量多2万公斤,求4、5两个月销量各多少万公斤?
18、(南宁08)随着绿城南宁近几年城市建设的快速发展,对花木的需求量逐年提高. 某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润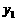 与投资量x成正比例关系,如图12-①所示;种植花卉的利润
与投资量x成正比例关系,如图12-①所示;种植花卉的利润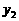 与投资量x成二次函数关系,如图12-②所示(注:利润与投资量的单位:万元).
与投资量x成二次函数关系,如图12-②所示(注:利润与投资量的单位:万元).
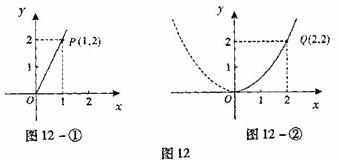
(1)分别求出利润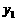 与
与 关于投资量x的函数关系式;
关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获得的最大利润是多少?
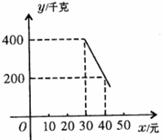
17、(十堰06)“健益”超市购进一批 元/千克的绿色食品,如果以
元/千克的绿色食品,如果以 元/千克销售,那么每天可售出
元/千克销售,那么每天可售出 千克.由销售经验知,每天销售量
千克.由销售经验知,每天销售量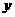 (千克)与销售单价
(千克)与销售单价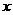 (元)(
(元)(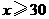 )存在如下图所示的一次函数关系.
)存在如下图所示的一次函数关系.
(1)试求出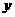 与
与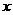 的函数关系式;
的函数关系式;
(2)设“健益”超市销售该绿色食品每天获得利润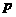 元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
(3)根据市场调查,该绿色食品每天可获利润不超过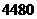 元,现该超市经理要求每天利润不得低于
元,现该超市经理要求每天利润不得低于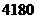 元,请你帮助该超市确定绿色食品销售单价
元,请你帮助该超市确定绿色食品销售单价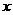 的范围(直接写出).
的范围(直接写出).
16、(07龙岩)如图,抛物线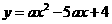 经过
经过 的三个顶点,已知
的三个顶点,已知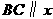 轴,点
轴,点 在
在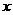 轴上,点
轴上,点 在
在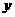 轴上,且
轴上,且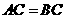 .
.
(1)求抛物线的对称轴;
(2)写出 三点的坐标并求抛物线的解析式;
三点的坐标并求抛物线的解析式;
(3)探究:若点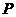 是抛物线对称轴上且在
是抛物线对称轴上且在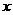 轴下方的动点,是否存在
轴下方的动点,是否存在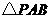 是等腰三角形.若存在,求出所有符合条件的点
是等腰三角形.若存在,求出所有符合条件的点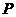 坐标;不存在,请说明理由.
坐标;不存在,请说明理由.
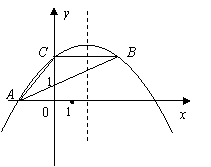
15、(08云南)如图,已知二次函数图象的顶点坐标为C(1,0),直线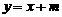 与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴
与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴 上.
上.
(1)求 的值及这个二次函数的关系式;
的值及这个二次函数的关系式;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作 轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为
轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为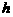 ,点P的横坐标为
,点P的横坐标为 ,求
,求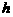 与
与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围;
的取值范围;
(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
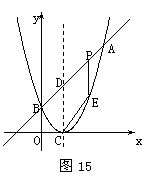
14、(海南08)如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2 与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E.(1)求m的值及该抛物线对应的函数关系式;
(2)求证:① CB=CE ;② D是BE的中点;
(3)若P(x,y)是该抛物线上的一个动点,是否存在这样的点P,使得PB=PE,若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由.
13、(海南05)如图,抛物线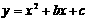 与
与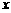 轴交于A(-1,0),B(3,0) 两点.
轴交于A(-1,0),B(3,0) 两点.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标;
(3)设(1)中抛物线交y 轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
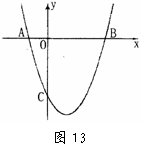
12、(08宁波)如图,□ABCD中,AB=4,点D的坐标是(0,8),以点C为顶点的抛物线y=ax2+bx+c经过x轴上的点A、B.
(1)求点A、B、C的坐标.
(2)若抛物线向上平移后恰好经过点D,求平移后抛物线的解析式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com