
题目列表(包括答案和解析)
2.(•赣州市)用“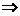 ”与“
”与“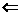 ”表示一种法则:(a
”表示一种法则:(a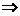 b)= -b,(a
b)= -b,(a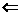 b)= -a,如(2
b)= -a,如(2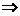 3)= -3,
3)= -3,
则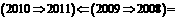 .
.
1.(•泰州市)让我们轻松一下,做一个数字游戏:
第一步:取一个自然数n1=5 ,计算n12+1得a1;
第二步:算出a1的各位数字之和得n2,计算n22+1得a2;
第三步:算出a2的各位数字之和得n3,再计算n23+1得a3;
…………
依此类推,则a=____________.
4.[答案]观察计算
(1)a+2;(2)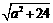 .
.
探索归纳
(1)① ;②
;② ;
;
(2)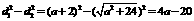 .
.
①当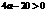 ,即
,即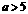 时,
时,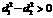 ,
,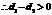 .
.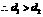 ;
;
②当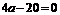 ,即
,即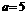 时,
时,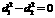 ,
,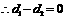 .
.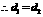 ;
;
③当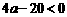 ,即
,即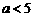 时,
时,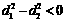 ,
,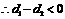 .
.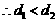 .
.
综上可知:当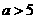 时,选方案二;
时,选方案二;
当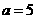 时,选方案一或方案二;
时,选方案一或方案二;
当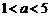 时,选方案一.
时,选方案一.
3.[解析]根据题目中存在的等量关系,容易填写出未知的量,然后建立w与x之间的函数关系式.
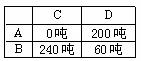
[答案]解:(1)填表

依题意得: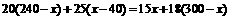 .
.
解得: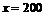 .
.
(2) w与x之间的函数关系为: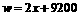 .
.
依题意得: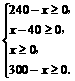 ,∴40≤
,∴40≤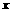 ≤240
≤240
在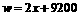 中,∵2>0,∴
中,∵2>0,∴ 随
随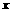 的增大而增大,
的增大而增大,
故当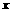 =40时,总运费最小,
=40时,总运费最小,
此时调运方案为如下表.
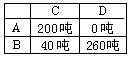
(3)由题意知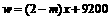
∴0< <2时,(2)中调运方案总运费最小;
<2时,(2)中调运方案总运费最小;
 =2时,在40≤
=2时,在40≤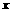 ≤240的前提下调运,方案的总运费不变;
≤240的前提下调运,方案的总运费不变;
2< <15时,
<15时,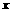 =240总运费最小,
=240总运费最小,
其调运方案如下表
2.[答案]解:(1) 四边形EFGH是正方形.
图(2)可以看作是由四块图(1)所示地砖绕C点按顺(逆)时针方向旋转90°后得到的,故CE=CF =CG.∴△CEF是等腰直角三角形.因此四边形EFGH是正方形.
(2)设CE=x, 则BE=0.4-x,每块地砖的费用为y,那么
y=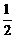 x
x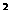 ×30+
×30+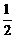 ×0.4×(0.4-x)×20+[0.16-
×0.4×(0.4-x)×20+[0.16-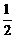 x
x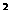 -
-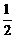 ×0.4×(0.4-x)×10] =10(x
×0.4×(0.4-x)×10] =10(x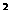 -0.2x+0.24)
=10[(x-0.1)2+0.23] (0<x<0.4) .
-0.2x+0.24)
=10[(x-0.1)2+0.23] (0<x<0.4) .
当x=0.1时,y有最小值,即费用为最省,此时CE=CF=0.1.
答:当CE=CF=0.1米时,总费用最省.
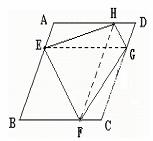
1.[答案]解:方案(1)
画法1:(1)过F作FH∥AD交AD于点H;(2)在DC上任取一点G连接EF、FG、GH、HE,则四边形EFGH就是所要画的四边形;
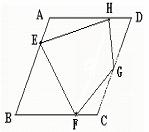
画法2:(1)过F作FH∥AB交AD于点H;(2)过E作EG∥AD交DC于点G连接EF、FG、GH、HE,则四边形EFGH就是所要画的四边形
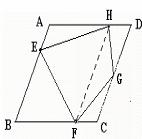
画法3:(1)在AD上取一点H,使DH=CF;(2)在CD上任取一点G连接EF、FG、GH、HE,则四边形EFGH就是所要画的四边形
方案(2)画法:(1)过M点作MP∥AB交AD于点P,
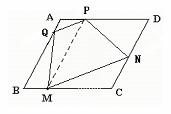
(2)在AB上取一点Q,连接PQ,
(3)过M作MN∥PQ交DC于点N,连接QM、PN、MN则四边形QMNP就是所要画的四边形
(本题答案不唯一,符合要求即可)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com