
题目列表(包括答案和解析)
9.已知抛物线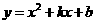 经过点
经过点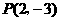 ,
,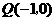 .
.
(1)求抛物线的解析式.
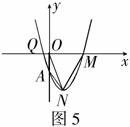
(2)设抛物线顶点为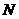 (如图5),与y轴交点为A.求
(如图5),与y轴交点为A.求 的值.
的值.
(3)设抛物线与x轴的另一个交点为M,求四边形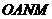 的面积.
的面积.
8.市政公司为绿化一段沿江风光带,计划购买甲、乙两种树苗共500株,甲种树苗每株50元,乙种树苗每株80元.有关统计表明:甲、乙两种树苗的成活率分别为90%和95%.
(1)若购买树苗共用了28 000元,求甲、乙两种树苗各多少株?
(2)若购买树苗的钱不超过34 000元,应如何选购树苗?
(3)若希望这批树苗的成活率不低于92%,且购买树苗的费用最低,应如何选购树苗.
7.某商场用36万元购进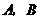 两种商品,销售完后共获利6万元,其进价和售价如下表:
两种商品,销售完后共获利6万元,其进价和售价如下表:
|
|
 |
 |
|
进价(元/件) |
1200 |
1000 |
|
售价(元/件) |
1380 |
1200 |
(注:获利=售价-进价)
(1)该商场购进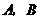 两种商品各多少件;
两种商品各多少件;
(2)商场第二次以原进价购进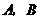 两种商品.购进
两种商品.购进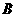 种商品的件数不变,而购进A种商品的件数是第一次的2倍,
种商品的件数不变,而购进A种商品的件数是第一次的2倍, 种商品按原售价出售,而
种商品按原售价出售,而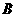 种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81 600元,
种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81 600元,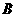 种商品最低售价为每件多少元?
种商品最低售价为每件多少元?
6.为净化空气,美化环境,市冷水滩区在许多街道和居民小区都种上了玉兰和樟树,冷水滩区新建的某住宅区内,计划投资1.8万元种玉兰树和樟树共80棵,已知某苗圃负责种活以上两种树苗的价格分别为:玉兰树300元/棵,樟树200元/棵,问可种玉兰树和樟树各多少棵?
5. 已知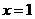 是一元二次方程
是一元二次方程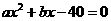 的一个解,且
的一个解,且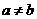 ,求
,求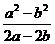 的值.
的值.
4.中国人民银行宣布,从2007年6月5日起,上调人民币存款利率,一年定期存款利率上调到3.06%.某人于2007年6月5日存入定期为1年的人民币5000元(到期后银行将扣除20%的利息锐).设到期后银行应向储户支付现金x元,则所列方程正确的是( )
(A)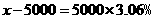
(B)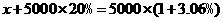
(C)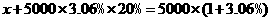
(D)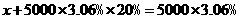
3.不等式组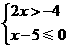 的解集是( )
的解集是( )
(A)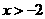 (B)
(B)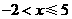
(C)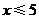 (D)无解
(D)无解
2.分式方程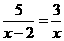 的解为
的解为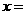 ____________.
____________.
1.方程组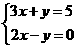 的解是____________.
的解是____________.
例19、(2004 重庆)如图,AB、CD是两个过江电缆的铁塔,塔AB高40米,AB的中点为P,塔底B距江面的垂直高度为6米。跨江电缆因重力自然下垂近似成抛物线形,为了保证过往船只的安全,电缆下垂的最低点距江面的高度不得少于30米。已知:人在距塔底B点西50米的地面E点恰好看到点E、P、C在一直线上;再向西前进150米后从地面F点恰好看到点F、A、C在一直线上。
 (1)求两铁塔轴线间的距离(即直线AB、CD间的距离);
(1)求两铁塔轴线间的距离(即直线AB、CD间的距离);
(2)若以点A为坐标原点,向东的水平方向为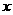 轴,取单位长度为1米,BA的延长方向为
轴,取单位长度为1米,BA的延长方向为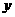 轴建立坐标系。求刚好满足最低高度要求的这个抛物线的解析式。
轴建立坐标系。求刚好满足最低高度要求的这个抛物线的解析式。
解:如图,AB=40米,BP=20米,BE=50米,BF=50+150=200(米)。
设CD的延长线交地平面于点H。
(1)设CH=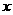 ,BH=
,BH=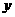
由△EBP∽△EHC得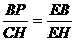 ,即
,即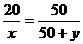 ………①
………①
由△FBA∽△FHC得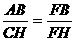 ,即
,即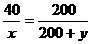 ……②
……②
由①②解得: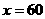 ,
,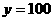
答:两铁塔轴线间的距离为100米。

(2)依题意建立坐标系如图,由(1)得CH=60米,C点比A点高20米,这时A、C两点的坐标为:A(0,0),C(100,20),设抛物线顶点为P(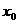 ,
,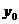 ),因为要求最低点高于地面为30-6=24(米),点A高度为40米,所以
),因为要求最低点高于地面为30-6=24(米),点A高度为40米,所以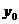 =-16。设过点A的抛物线解析式为
=-16。设过点A的抛物线解析式为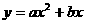 (
(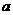 >0),则该抛物线满足
>0),则该抛物线满足
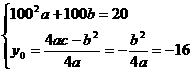
化简得: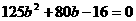
解得: ,
,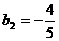
∵抛物线的对称轴在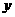 轴的右侧,有
轴的右侧,有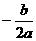 >0,而
>0,而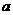 >0
>0
∴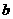 <0,故
<0,故 舍去
舍去
把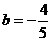 代入前式得:
代入前式得: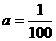
∴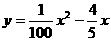
答:所求抛物线的解析式为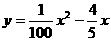 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com