
题目列表(包括答案和解析)
7.⑴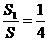 ;⑵
;⑵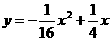 (0<
(0< <4);⑶不存在点D,使得S1>
<4);⑶不存在点D,使得S1>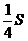 成立。
成立。
6.⑴证△ABE∽△ACD;⑵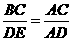 (或
(或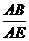 )。先证△ABE∽△ACD,再证△BAC∽△EAD。
)。先证△ABE∽△ACD,再证△BAC∽△EAD。
5.⑴画图(要求对应点在水平位置上,宽度保持一致)。
⑵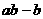 ,
,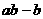 ,
,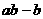 。
。


⑶猜想:依据前面的有关计算,可以猜想草地的面积仍然是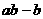 。方案:①将“小路”
。方案:①将“小路”
沿着左右两个边界“剪去”;②将左侧的草地向右平移一个单位;③得到一个新的矩形(如图)。理由略。
3.△OAB在变换中,A、B点的纵坐标保持不变,横坐标按2倍递增,∴A4 (16,3),
B4(32,0)。按此规律,显然An (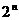 ,
,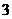 ),Bn(
),Bn(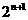 ,
, )。
)。
4.依题意可猜想:当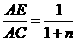 时,有
时,有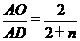 成立。
成立。
过点D作DF∥BC交AC于点F,∵D为BC边的中点,∴F是EC的中点
由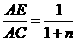 ,可知
,可知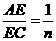 。
。
∴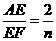 ,
,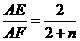 ,∴
,∴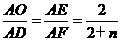 。
。
2.①、②、④;
1.AB=CD或AB=CD;
13.(山西省中考题)如图,已知圆心A(0,3),⊙A与 轴相切,⊙B的圆心在
轴相切,⊙B的圆心在 轴
轴
的正半轴上,且⊙B与⊙A外切于点P,两圆的公切线MP交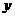 轴于点M,交
轴于点M,交 轴于点N。
轴于点N。
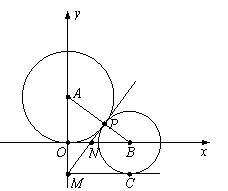 ⑴若
⑴若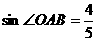 ,求直线MP的解析式及经过
,求直线MP的解析式及经过
M、N、B三点的抛物线的解析式。
⑵若⊙A的位置大小不变,⊙B的圆心在 轴的正
轴的正
半轴上移动,并使⊙B与⊙A始终外切,过M作⊙B的
切线MC,切点为C。在此变化过程中探究:
①四边形OMCB是什么四边形,对你的结论加以
证明;
②经过M、N、B三点的抛物线内是否存在以BN为腰的等腰三角形?若存在,表示出
来;若不存在,说明理由。
|
|
12.(江苏无锡市中考题)已知抛物线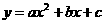 (
(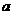 <0)
<0) 轴交于A、B两点,点A在
轴交于A、B两点,点A在 轴的负半轴上,点B在
轴的负半轴上,点B在 轴的正半轴上,又此抛物线交
轴的正半轴上,又此抛物线交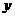 轴于点C,连AC、BC,且满足△OAC的面积与△OBC的面积之差等于两线段OA与OB的积(即S△OAC-S△OBC=
轴于点C,连AC、BC,且满足△OAC的面积与△OBC的面积之差等于两线段OA与OB的积(即S△OAC-S△OBC=
OA·OB)。
⑴求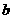 的值;
的值;
⑵若tan∠CAB=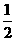 ,抛物线的顶点为点P,是否存在这样的抛物线,使得△PAB的外接圆半径为
,抛物线的顶点为点P,是否存在这样的抛物线,使得△PAB的外接圆半径为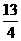 ?若存在,求出这样的抛物线的解析式;若不存在,请说明理由。
?若存在,求出这样的抛物线的解析式;若不存在,请说明理由。
11.(北京市中考题)已知:抛物线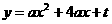 与
与 轴的一个交点为A(
轴的一个交点为A(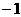 ,
, )。
)。
⑴求抛物线与 轴的另一个交点B的坐标;
轴的另一个交点B的坐标;
⑵D是抛物线与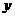 轴的交点,C是抛物线上的一点,且以AB为一底的梯形ABCD的
轴的交点,C是抛物线上的一点,且以AB为一底的梯形ABCD的
面积为9,求此抛物线的解析式;
⑶E是第二象限内到 轴、
轴、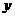 轴的距离的比为5∶2的点,如果点E在⑵中的抛物线上,
轴的距离的比为5∶2的点,如果点E在⑵中的抛物线上,
且它与点A在此抛物线对称轴的同侧,问:在抛物线的对称轴上是否存在点P,使△APE的周长最小?若存在,求出点P的坐标;若不存在,请说明理由。
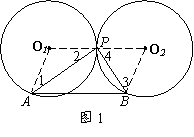
10.(山西太原中考题)⑴操作并观察:如图1,两个半径为 的等圆⊙O1与⊙O2外切于点P。将三角板的直角顶点放在点P,再将三角形绕点P旋转,使三角板的两直角边中的一边PA与⊙O1相交于A,另一边PB与⊙O2相交于点B(转动中直角边与两圆都不相切)。在转动过程中,线段AB的长与半径
的等圆⊙O1与⊙O2外切于点P。将三角板的直角顶点放在点P,再将三角形绕点P旋转,使三角板的两直角边中的一边PA与⊙O1相交于A,另一边PB与⊙O2相交于点B(转动中直角边与两圆都不相切)。在转动过程中,线段AB的长与半径 之间有什么关系?请回答并证明你得到的结论;
之间有什么关系?请回答并证明你得到的结论;
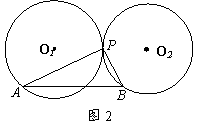
⑵如图2,设⊙O1与⊙O2外切于点P,半径分别为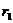 、
、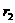 (
(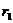 >
>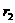 ),重复⑴中的操作过程,观察线段AB的长度与
),重复⑴中的操作过程,观察线段AB的长度与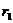 、
、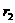 之间有怎样的关系,并说明理由。
之间有怎样的关系,并说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com