
题目列表(包括答案和解析)
20.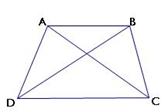 (10分)如图,AD=BC,∠ADC=∠BCD;
(10分)如图,AD=BC,∠ADC=∠BCD;
求证:∠BDC=∠ACD
19.(8分)化简求值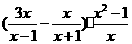 其中
其中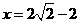
18.(8分)解分式方程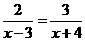
26.(本题满分13分)
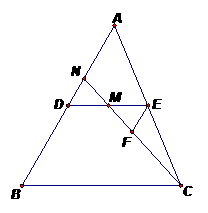
解:(1)过E点作EF∥AB交CN于F,
由△CEF-△CAN知:
2EF=AN - 1分-
又由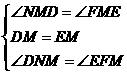
知△EFM≌△DNM(ASA)
所以EF=DN - 2分-
所以AN=2DN - 3分-
设△DNM DM边上的高为h,则△ADE DE边上的高为3h
DM=ME=x
则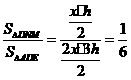
故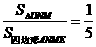 - 4分-
- 4分-
(2)由于该同学设计制作均属同一材料,且厚度不计
故等腰梯形ABCD的面积与(1)中△ABC的面积相等
 则:
则: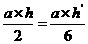
故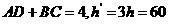 - 5分-
- 5分-
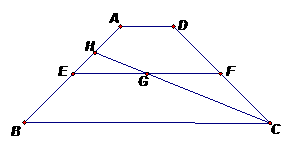
设等腰梯形ABCD中AD=x
则BC=4-x
由△HEG-△HBC
设EG边上的高为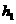
则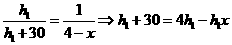
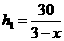 - 6分-
- 6分-
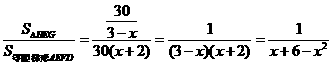 - 7分-
- 7分-
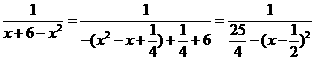 - 8分-
- 8分-
故当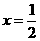 时,
时,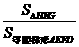 的比值最大,为
的比值最大,为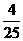
即当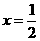 时,
时,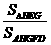 的比值最大,为
的比值最大,为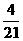 - 9分-
- 9分-
(3)过E点作EI∥AB交NG于I,过C点作CQ∥AB交NG延长线于Q,
设BC=2,ND=x
由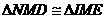 得:
得:
IE=ND
又△DCG-△IEM
知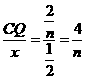
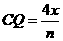 - 10分-
- 10分-
又由梯形中位线性质:
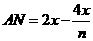
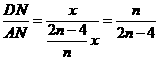
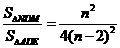
故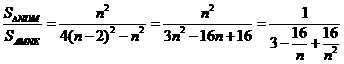 - 11分-
- 11分-
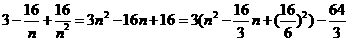
故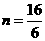 时, 为函数
时, 为函数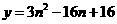 的对称轴,
的对称轴,
故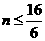 时,函数单调递减,故此时
时,函数单调递减,故此时
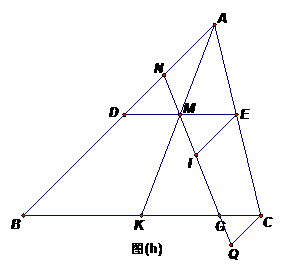
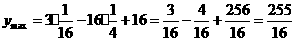 - 12分-
- 12分-
故存在,此时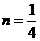 ,
,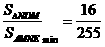 - 13分-
- 13分-
(训练二)2005年厦门质检
25.(本题满分12分)
解:(1)共2对相似三角形
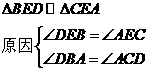 -1分-
-1分-

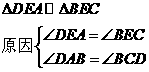 -2分-
-2分-
(2)①AD>AC
AD>AE>AC -3分-
②AD<AC
AD<AE<AC -4分-
(3)①证明: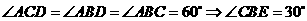
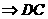 ∥
∥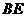
又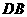 ∥
∥
∴四边形CDBE为平行四边形 -5分-
②∵ PA⊥OP, PQ⊥OA
∴ △OPQ∽△OAP
设:△OPQ的面积为s1,则
= - 6分-
即: =
化简得:2n4+2k2-k n4-4k=0 -7分-
(k-2)(2k-n4)=0
∴k=2或k=(舍去) -8分-
∴当n是小于20的整数时,k=2.
∵ BC2=n2+m2=n2+
又m>0,k=2,
∴ n是大于0且小于20的整数
当n=1时,OP2=5
当n=2时,OP2=5
当n=3时,BC2=32+=9+= -10分-
当n是大于3且小于20的整数时,
即当n=4、5、6、…、19时,OP2得值分别是:
42+、52+、62+、…、192+
∵192+>182+>…>32+>5 - 11分-
 ∴ BC2的最小值是5. - 12分-
∴ BC2的最小值是5. - 12分-
24.(本题满分12分)
解:(1)表中空白处填写项目依次为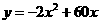 ;15;450.
-6分-
;15;450.
-6分-
表中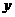 取最大值时的设计示意图分别为:
取最大值时的设计示意图分别为:
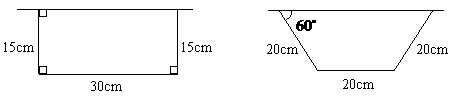
-8分-
(2)小华的说法不正确. -10分-
因为腰长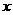 大于30cm时,符合题意的等腰梯形不存在,所以
大于30cm时,符合题意的等腰梯形不存在,所以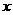 的取值范围不能超过30cm,因此研究性学习小组画出的图象是正确的.
-12分-
的取值范围不能超过30cm,因此研究性学习小组画出的图象是正确的.
-12分-
23.(本题满分10分)
解:(1)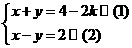 ,(1)+(2)得:
,(1)+(2)得:
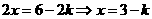 -2分-
-2分-
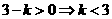 -3分-
-3分-
(2)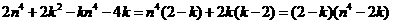 -4分-
-4分-
∵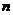 是正整数
是正整数
∴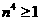
∴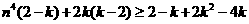 -5分-
-5分-
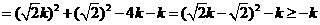
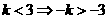 -6分-
-6分-
(Ⅰ)当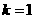 时,
时,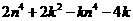
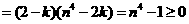
当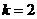 时,
时,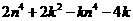
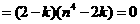 -7分-
-7分-
(Ⅱ)当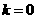 时,
时,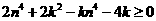 -8分-
-8分-
(Ⅲ)当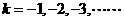 时,
时,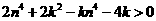 -9分-
-9分-
∴综上有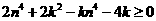 -10分-
-10分-
22.(本题满分10分)
解:(1)当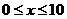 时,
时,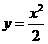 -1分-
-1分-
当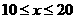 时,
时,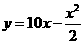 -2分-
-2分-
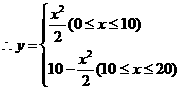 -3分-
-3分-
(2)如下图所示:(图示2分)
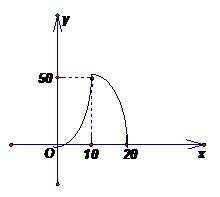
(3)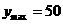 -7分-
-7分-
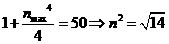 -9分-
-9分-
又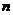 为正整数
为正整数
∴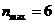 -10分-
-10分-
21.(本题满分10分)
(1)
|
|
第1次 |
第2次 |
第3次 |
第4次 |
………… |
第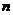 次 次 |
 |
 |
 |
 |
 |
………… |
|
|
1 |
5 |
17 |
53 |
161 |
………… |
|
(前四空每空各0.5 分,第五空1分)
(2)
后一个三角形的个数为前一个三角形个数的3倍加2
(答案允许不同,言之成立即可,满分2分)
(3)根据你的判断,经过第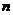 次变换后,三角形的个数是
次变换后,三角形的个数是 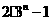 .
.
(第三小题满分3分)
20.(本题满分8分)
解:(1)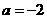 ,则
,则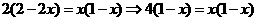 -1分-
-1分-
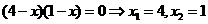 -2分-
-2分-
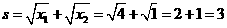 -3分-
-3分-
(2)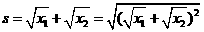 -4分-
-4分-
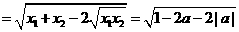 -5分-
-5分-
又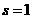
∴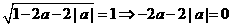
∴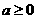 -6分-
-6分-
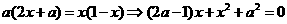
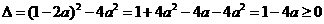
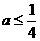 -7分-
-7分-
∴综上有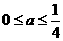 -8分-
-8分-
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com