
题目列表(包括答案和解析)
例3 已知抛物线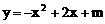 交x轴于两点
交x轴于两点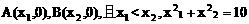 .
.
又点P(4,n)在该抛物线上,设抛物线的顶点是C,求 的面积S。
的面积S。
分析:将 分成两个
分成两个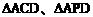 ,需求底边AD的长及相应的高,即点C、点P的纵坐标。为此,首先需确定抛物线的解析式。
,需求底边AD的长及相应的高,即点C、点P的纵坐标。为此,首先需确定抛物线的解析式。
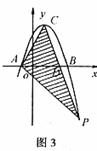
解: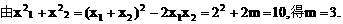
所以抛物线是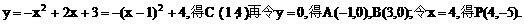
又由顶点C(1,4),P(4,-5)可得直线PC:y=-3x+7.再令y=0,得PC与x轴交点为
D(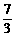 ,0).
,0).
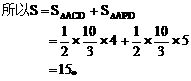
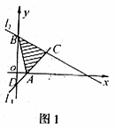
例4 设直线l:y=2x+2交x轴于点A、交y轴于点B,一条抛物线过点A、点B及点(2,2),且与x轴的另一交点为D,顶点为C。求四边形ABCD的面积。
简解:将四边形分成三个三角形: 易由直线l:y=2x+2,得A(-1,0),B(0,2).
易由直线l:y=2x+2,得A(-1,0),B(0,2).
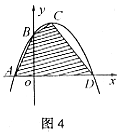
又过A、B及(2,2)的抛物线为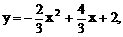 则顶点为
则顶点为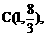 与x轴的另一交点为D(3,0)。
与x轴的另一交点为D(3,0)。
所以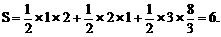
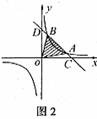
解:画出示意图,直接求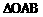 的底边AB长和相应的高,比较困难。现割补法进行转化,记直线交x轴于点C,交y轴于点D,则所求面积
的底边AB长和相应的高,比较困难。现割补法进行转化,记直线交x轴于点C,交y轴于点D,则所求面积 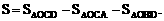
在y=-x+5中,分别令y=0,x=0,得C(5,0),D(0,5)。又由 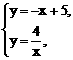
得A(4,1),B(1,4)
从而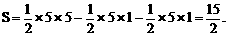
解:画出略图.可见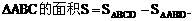 只要求出底边长和高(点C、A的横坐标).
只要求出底边长和高(点C、A的横坐标).
在
得C(3,2)
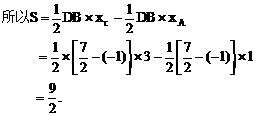
3.(08贵阳)如图,已知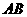 是⊙O的直径,点
是⊙O的直径,点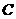 在⊙O上,且
在⊙O上,且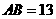 ,
,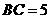 .
.
(1)求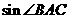 的值;
的值;
 (2)如果
(2)如果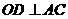 ,垂足为
,垂足为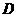 ,求
,求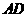 的长;
的长;
(3)求图中阴影部分的面积(精确到0.1).
﹡
﹡4.(07贵阳)如图,从一个直径是2的圆形铁皮中剪下一个圆心角为 的扇形.
的扇形.
(1)求这个扇形的面积(结果保留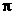 );
);
(2)在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由.
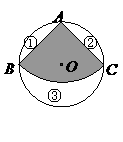 (3)当⊙O的半径
(3)当⊙O的半径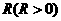 为任意值时,(2)中的结论是否仍然成立?请说明理由.
为任意值时,(2)中的结论是否仍然成立?请说明理由.
2. (08厦门)如图,在矩形空地上铺4块扇形草地.若扇形的半径均为 米,圆心角均为
米,圆心角均为 ,则铺上的草地共有
平方米.
,则铺上的草地共有
平方米.


1. (08孝感) 中,
中,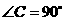 ,
,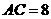 ,
,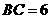 ,两等圆⊙A,⊙B外切,那么图中两个扇形(即阴影部分)的面积之和为( )
,两等圆⊙A,⊙B外切,那么图中两个扇形(即阴影部分)的面积之和为( )
A.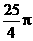 B.
B.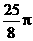 C.
C.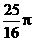 D.
D.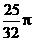
4. 圆锥的侧面积公式:S=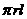 .(其中
.(其中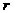 为
的半径,
为
的半径,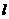 为 的长)
为 的长)
[典例精析]
例1 (08金华)如图,CD切⊙O于点D,连结OC,交⊙O于点B,过点B作弦AB⊥OD,
点E为垂足,已知⊙O的半径为10,sin∠COD =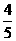 .(1)求弦AB的长;(2)CD的长;
.(1)求弦AB的长;(2)CD的长;
(3)劣弧AB的长.(结果保留三个有效数字,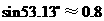 ,
,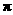 ≈3.142)
≈3.142)
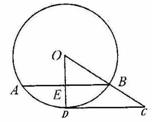
例2 (08南昌)如图,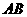 为⊙O的直径,
为⊙O的直径,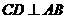 于点
于点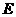 ,交⊙O于点
,交⊙O于点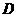 ,
,
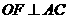 于点
于点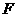 .
.
(1)请写出三条与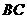 有关的正确结论;
有关的正确结论;
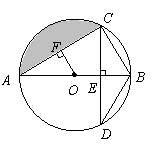 (2)当
(2)当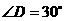 ,
,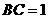 时,求圆中阴影部分的面积.
时,求圆中阴影部分的面积.
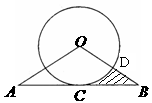
例3 (08庆阳)如图,线段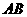 与⊙O相切于点
与⊙O相切于点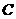 ,连结
,连结 、
、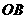 ,
,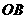 交⊙O于点D,已知
交⊙O于点D,已知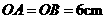 ,
,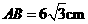 .
.
求(1)⊙O的半径; (2)图中阴影部分的面积.
[中考演练]
3. 圆柱的侧面积公式:S=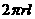 .(其中
.(其中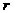 为
的半径,
为
的半径,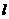 为 的高)
为 的高)
2. 圆的面积为
,1°的圆心角所在的扇形面积为
,n°的圆心角所在的扇形面积为S= 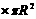 = = .
= = .
1. 圆的周长为 ,1°的圆心角所对的弧长为 ,n°的圆心角所对
的弧长为 ,弧长公式为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com