
题目列表(包括答案和解析)
3、已知a、b、c成等比数列,a、x、b和b、y、c都成等差数列,且xy≠0,那么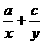 的值为( )。
的值为( )。
(A)1 (B)2 (C)3 (D)4
2、已知l、m、n为两两垂直且异面的三条直线,过l作平面α与m垂直,则直线n与平面α的关系是( )。
(A)n//α (B)n//α或n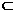 α
α
(C)n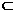 α或n不平行于α (D)n
α或n不平行于α (D)n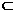 α
α
1、函数y=cos4x-sin4x图象的一条对称轴方程是( )。
(A)x=-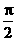 (B)x=-
(B)x=-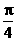 (C)x=
(C)x=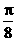 (D)x=
(D)x=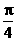
22.(本小题满分14分)
[理]已知函数f(x)对任意的x∈R都有f(x)=1-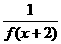 ,且f(0)=m(m>0,且m≠1)。
,且f(0)=m(m>0,且m≠1)。
(Ⅰ)求f(2)及f(4)的值;
(Ⅱ)求证:f(x)是周期函数,并求出它的一个周期;
(Ⅲ)若f(1)=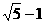 ,求f(22n+7)的值(n∈N)。
,求f(22n+7)的值(n∈N)。
[文]已知函数f(x)=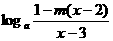 (a>0,a≠1),对定义域内的任意x都有f(2-x)+f(2+x)=0。
(a>0,a≠1),对定义域内的任意x都有f(2-x)+f(2+x)=0。
(Ⅰ)求实数m的值;
(Ⅱ)若当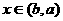 时,f(x)的取值范围恰为
时,f(x)的取值范围恰为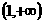 ,求实数a、b的值。
,求实数a、b的值。
21.(本小题满分12分)
[理]已知数列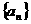 的前三项依次为
的前三项依次为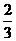 ,
,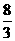 ,
,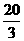 ,前n项和为S n,且Sn=an3+bn2+cn(a、b、c∈R)。
,前n项和为S n,且Sn=an3+bn2+cn(a、b、c∈R)。
(Ⅰ)求S n的表达式;
(Ⅱ)若数列 满足b n=an+1-an,
满足b n=an+1-an,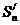 为数列
为数列 的前n项和,试求使得|
的前n项和,试求使得|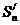 -2003|取得最小值的n的值;
-2003|取得最小值的n的值;
 (Ⅲ)若Tn=
(Ⅲ)若Tn=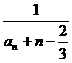 ,求证:
,求证: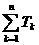 <
<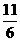 (n≥2)。
(n≥2)。
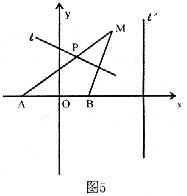
[文]如图5,A、B是两个定点,且|AB|=4。动点M到
A点的距离是6,线段MB的垂直平分线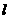 交MA于点P。
交MA于点P。
直线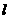 ′垂直于直线AB,且B点到
′垂直于直线AB,且B点到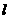 ′的距离为
′的距离为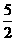 。若以
。若以
AB所在直线为x轴,AB的垂直平分线为y轴建立直角坐标系。
(Ⅰ)求证:点P点到点B的距离与到直线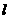 ′的距离之比为定值;
′的距离之比为定值;
(Ⅱ)若点P到A、B两点的距离之积为m,当m取最大值时,求P点的坐标。
20.(本小题满分12分)
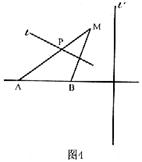 [理]如图4,A、B是两个定点,且|AB|=4。动点M到
[理]如图4,A、B是两个定点,且|AB|=4。动点M到
A点的距离是6,线段MB的垂直平分线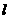 交MA于点P
交MA于点P
,直线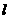 ′垂直于直线AB,且B点到
′垂直于直线AB,且B点到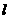 ′的距离为
′的距离为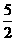 。若
。若
以AB所在直线为x轴,AB的垂平分线为y轴建直角坐标系。
(Ⅰ)求证:点P到点B的距离与到直线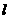 ′的距离之比为定值;
′的距离之比为定值;
(Ⅱ)若点P到A、B两点的距离之积为m,当m取最大值时,
求P点的坐标。
[文]设各项均为正数的数列的前n项和为S n,且存在正数t,使得对所有正整数n,都有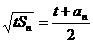 。
。
(Ⅰ)求数列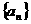 的通项公式;
的通项公式;
(Ⅱ)如果
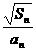 <t,求t的取值范围。
<t,求t的取值范围。
19.(本小题满分12分)
一艘轮船在航行过程中的燃料费与它的速度立方成正比例关系,其它与速度无关的费用为每小时96元。已知在速度为每小时10千米时,每小时的燃料费是6元。要使行驶1千米所需的费用总和最小,这艘轮船的速度应确定为每小时多少千米?
18.(本小题满分12分)
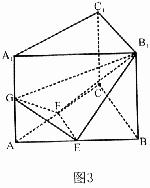 如图3,在直三棱柱ABC-A 1B 1C
1中,AC=BC=A 1A=2,∠ACB=90°,E、F、G分别是AB、AC、AA1的中点。
如图3,在直三棱柱ABC-A 1B 1C
1中,AC=BC=A 1A=2,∠ACB=90°,E、F、G分别是AB、AC、AA1的中点。
(Ⅰ)求证:B 1C1∥平面EFG;
(Ⅱ)求三棱锥B1-EFG的体积。
17.(本小题满分12分)
在复平面上复数z1=2+i对应的点Z1,将向量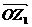 沿顺时针方向旋转锐角
沿顺时针方向旋转锐角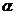 所得向量
所得向量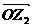 对应的复数z2,且tg
对应的复数z2,且tg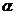 =
=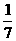 。若△ABC的内角A=argz1,B=argz2最长边为1。
。若△ABC的内角A=argz1,B=argz2最长边为1。
(Ⅰ)求角C的大小;
(Ⅱ)求△ABC的最短边的长。
16.设双曲线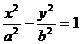 (a>0,b>0)的右准线与两条渐近线相交于A、B两点,F为右焦点,以AB为直径的圆恰过点F,则双曲线的离心率为_________。
(a>0,b>0)的右准线与两条渐近线相交于A、B两点,F为右焦点,以AB为直径的圆恰过点F,则双曲线的离心率为_________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com