
题目列表(包括答案和解析)
42、按复利计算利息的一种储蓄,本金为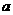 元,每期利率为
元,每期利率为 ,设本利和为
,设本利和为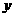 ,存期为
,存期为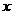 ,写出本利和
,写出本利和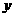 随存期
随存期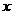 变化的函数式,如果存入本金1000元,每期利率2.25%,试计算5期后的本利和是多少?
变化的函数式,如果存入本金1000元,每期利率2.25%,试计算5期后的本利和是多少?
解:已知本金为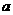 元
元
1期后的本利和为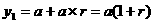 ;
;
2期后的本利和为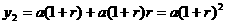 ;
;
3期后的本利和为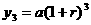 ;……
;……
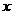 期后的本利和为
期后的本利和为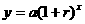
将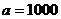 (元),
(元), =2.25%,
=2.25%, 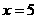 代入上式得
代入上式得
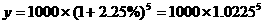
由计算器算得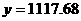 (元) 答:复利函数式为
(元) 答:复利函数式为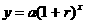 ,
,
5期后的本利和为1117.68元
评述:此题解答的过程体现了解题的思路,再现了探究问题的过程,容易被学生接受。
41、已知椭圆C: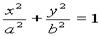 (a>b>0)的长轴两端点为A、B,
(1)过焦点F作垂直于长轴的弦PP′,当tg∠APB=
(a>b>0)的长轴两端点为A、B,
(1)过焦点F作垂直于长轴的弦PP′,当tg∠APB=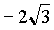 时,求C的离心率;
(2)如果C上存在一点Q,且∠AQB=1200,求C的离心率的范围。
解:(1)设F为右焦点;P在x轴下方,横坐标为c,则纵坐标为
时,求C的离心率;
(2)如果C上存在一点Q,且∠AQB=1200,求C的离心率的范围。
解:(1)设F为右焦点;P在x轴下方,横坐标为c,则纵坐标为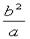 .
kPA=
.
kPA=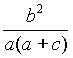 ,kPB=
,kPB=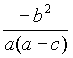 .
∴tg∠APB=
.
∴tg∠APB=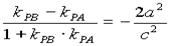 ,∴
,∴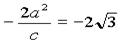 ,∴e=
,∴e=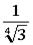 .
(2)设θ(x,y),由对称性,不妨设θ在x轴上方,即y>0.
kAQ=
.
(2)设θ(x,y),由对称性,不妨设θ在x轴上方,即y>0.
kAQ=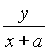 ,kBQ=
,kBQ=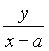 ,∴
,∴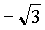 =tg∠AQB=
=tg∠AQB=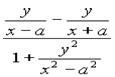 .
∴
.
∴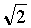 =(x2+y2-a2)+2ay=0.
此方程与椭圆方程联立,可求出y=0或
=(x2+y2-a2)+2ay=0.
此方程与椭圆方程联立,可求出y=0或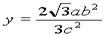 .由y=0,得Q与A或B重合,舍去.当
.由y=0,得Q与A或B重合,舍去.当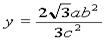 时,由Q在椭圆上半部.
∴
时,由Q在椭圆上半部.
∴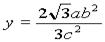 ≤b,∴
≤b,∴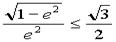 ,∴e∈
,∴e∈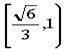 .
.
40、过椭圆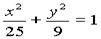 的左焦点F1的弦AB,过A,B分别向左准线引垂线,垂足分别为M,N,当线段MN最大时,求直线AB的方程。
解:由已知方程得F1(-4,0),设直线AB方程:y = tg
的左焦点F1的弦AB,过A,B分别向左准线引垂线,垂足分别为M,N,当线段MN最大时,求直线AB的方程。
解:由已知方程得F1(-4,0),设直线AB方程:y = tg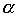 (x+4),代入椭圆方程
(x+4),代入椭圆方程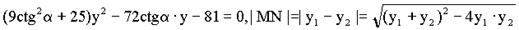 =
=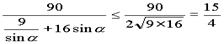 ,当sin
,当sin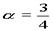 时,|MN|最大
时,|MN|最大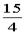 ,
,
此时 ∴直线方程为:
∴直线方程为: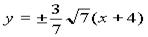 .
.
39、某渔场养鱼,鱼的重量增长率第一年为400%,以后每年重量增长率都是前一年的三分之一。同时鱼每年要损失预计重量的10%。预计养鱼的费用第一年是鱼苗成本的20%,以后每年的费用M(t)与年数t满足关系式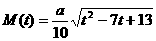 (其中
(其中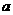 为鱼苗成本,
为鱼苗成本,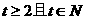 )。问该渔场的鱼养几年后全部捕捞,鱼的产值高且费用较少(设鱼苗价30元/斤,成鱼市场价7元/斤)。
)。问该渔场的鱼养几年后全部捕捞,鱼的产值高且费用较少(设鱼苗价30元/斤,成鱼市场价7元/斤)。
解:设第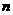 年鱼的产值
年鱼的产值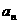 为最高。p为鱼苗总重量,则
为最高。p为鱼苗总重量,则
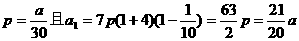 ,
,
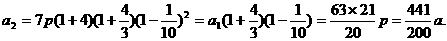
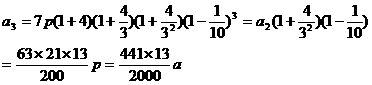
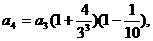 ……,
……,
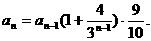
当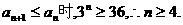
即第4年鱼的产值最高;另一方面,
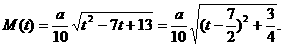
当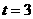 或4时,
或4时,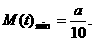
下面比较第4年比第3年增加的产值G与该年投入的费用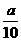 的大小。
的大小。
若G≠0则取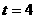 ;
;
若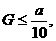 则取
则取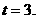
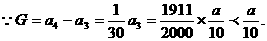
∴取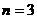 ,即该渔场三年后捕捞,鱼的总产值高且费用较少。
,即该渔场三年后捕捞,鱼的总产值高且费用较少。
38、铁道机车运行1小时所需的成本由两部分组成,固定部分为 元,变动部分与运行速度V(千米/小时)的平方成正比。比例系数为k(k≠0)。如果机车匀速从甲站开往乙站,为使成本最省应以怎样的速度运行?
元,变动部分与运行速度V(千米/小时)的平方成正比。比例系数为k(k≠0)。如果机车匀速从甲站开往乙站,为使成本最省应以怎样的速度运行?
解:设以速度V匀速运行成本最省,甲、乙两站相距S千米,则机车匀速从甲站到乙站所需时间为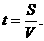 总成本为
总成本为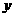 元。
元。
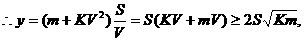
仅当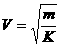 时,
时,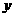 有最小值,
有最小值,
故机车以速度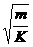 千米/小时匀速运行时,成本最省。
千米/小时匀速运行时,成本最省。
37、某市1994年底人口为20万,人均住房面积为8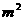 ,计划1998年底人均住房面积达10
,计划1998年底人均住房面积达10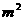 。如果该市每年人口平均增长率控制在1%,要实现上述计划,这个城市每年平均至少要新增住房面积多少万
。如果该市每年人口平均增长率控制在1%,要实现上述计划,这个城市每年平均至少要新增住房面积多少万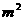 (结果以万
(结果以万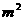 为单位,保留两位小数)。
为单位,保留两位小数)。
解:设平均每年至少要新增住房面积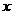 万
万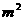 。四年共新增住房面积4
。四年共新增住房面积4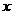 万
万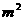 。此时住房总面积应为
。此时住房总面积应为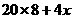 万
万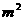 。另一方面,到1998年底总人口为20(1+1%)4万。按人均10
。另一方面,到1998年底总人口为20(1+1%)4万。按人均10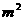 计,1998年底应有住房面积为20×10×(1+1%)4万
计,1998年底应有住房面积为20×10×(1+1%)4万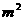 。据题意有:
。据题意有:
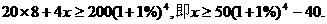
因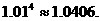 故
故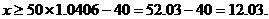 即
即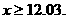
故该城市每年至少要新增住房面积12、03万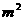 ,才可达人均住房面积10
,才可达人均住房面积10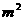 的目标。
的目标。
36、某企业在今年年初向银行贷款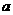 万元,年利率为
万元,年利率为 ;从今年年末开始,每年末向银行偿还一定的金额,预计五年内还清,问每年末平均偿还的金额应是多少?
;从今年年末开始,每年末向银行偿还一定的金额,预计五年内还清,问每年末平均偿还的金额应是多少?
解:设平均每年末应向银行偿还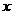 万元,则每年尚欠银行款依次为:
万元,则每年尚欠银行款依次为:
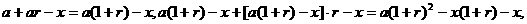
……
第五年欠款应等于零,即:
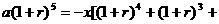 …
…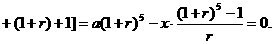
∴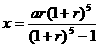 故平均每年末向银行偿还金额
故平均每年末向银行偿还金额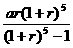 万元。
万元。
35、20个劳动力种50亩地,这些地可种蔬菜、棉花、水稻。这些作物每亩地所需劳力和预计产值如下表。应怎样计划才能使每亩地都能种上作物(水稻必种),所有劳力都有工作且作物预计总产值达最高?
|
作物 |
劳力/亩 |
产值/亩 |
|
蔬菜 |
1/2 |
0.6万元 |
|
棉花 |
1/3 |
0.5万元 |
|
水稻 |
1/4 |
0.3万元 |
解:设种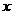 亩水稻(0<x≤50),
亩水稻(0<x≤50),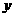 亩棉花(0<x≤50)时,总产值为
亩棉花(0<x≤50)时,总产值为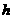 且每个劳力都有工作。
且每个劳力都有工作。
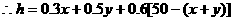 且
且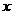 、
、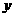 满足
满足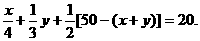
即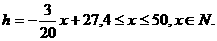
欲使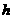 为最大,则
为最大,则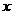 应为最小,故当
应为最小,故当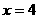 (亩)时,
(亩)时,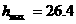 万元,此时
万元,此时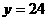 (亩)。
(亩)。
故安排1人种4亩水稻,8人种24亩棉花,11人种22亩蔬菜时农作物总产值最高且每个劳力都有工作。
34、进货原价为80元的商品400个,按90元一个售出时,可全部卖出。已知这种商品每个涨价一元,其销售数就减少20个,问售价应为多少时所获得利润最大?
解:设售价为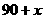 元时利润为
元时利润为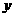 ,此时售量为
,此时售量为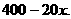
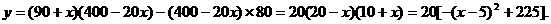
当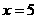 时,
时,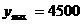 (元)。
(元)。
答:售价为95元时获利最大,其最大值为4500元。
33、在一个每边长均为1的正三棱锥内部有13个点,其中任三点不共线,任四点不共面,试证:其中至少有一个以这些点中的四个点为顶点的三棱锥,其体积V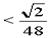
证明:设棱长均为1的正三棱锥为A-BCD,AO是它的高,今在AO上取一点O1,使O1A=O1B=O1C=O1D,可求得OB=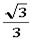 ,AO=
,AO=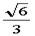 ,
,
进而求得O1A=O1B=O1C=O1D=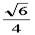 ;
;
以O1为点,以A-BCD得四个面为底面的四个三棱锥显然等积,且V'=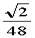 ;
;
在三棱锥内部的13个点,因为其中任三点不共线,任四点不共面,由抽屉原理,至少有四点落在以O1为顶点的四个小三棱锥的同一个三棱锥内,那幺这四点为顶点的三棱锥的体积V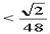 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com