
题目列表(包括答案和解析)
[例题示范]
1、成等差数列的四个数之和为26,第二数和第三数之积为40,求这四个数.
解:设四个数为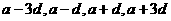
则: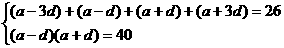
由①: 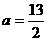 代入②得:
代入②得: 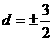
∴ 四个数为2,5,8,11或11,8,5,2.
22.(本题满分18分)本题共有3个小题,第1小题满分5分,
第2小题满分5分,第3小题满分8分.
已知函数 ,
,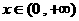 .
.
(1)作出函数 的大致图象并根据图象写出函数
的大致图象并根据图象写出函数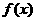 的单调区间;
的单调区间;
(2)(理)证明:当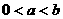 且
且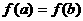 时,
时, ;
;
(2)(文)设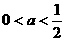 ,
,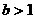 ,试比较
,试比较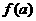 与
与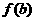 的大小;
的大小;
(3)(理)若存在实数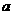 ,
,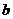 (
(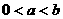 ),使得函数
),使得函数 在
在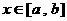 上的函数的值域为
上的函数的值域为 (
(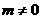 ),求实数
),求实数 的取值范围;
的取值范围;
(3)(文)是否存在实数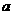 ,
,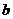 (
(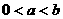 ),使得函数
),使得函数 在
在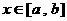 上的值域也是
上的值域也是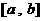 .若存在,求出
.若存在,求出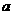 ,
,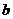 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
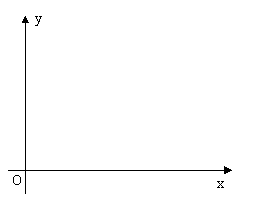
20.(本题满分14分)本题共有2个小题,第1题满分6分,
第2小题满分8分.
如图,已知点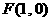 ,点
,点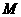 在
在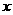 轴上,点
轴上,点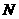 在
在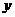 轴上,且
轴上,且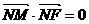 ,点
,点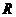 满足
满足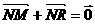 .
.
(1)求动点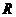 的轨迹
的轨迹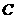 的方程;
的方程;
(2)(理)过点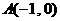 作斜率为
作斜率为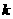 的直线
的直线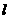 交轨迹
交轨迹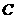 于
于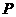 、
、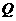 两点,且
两点,且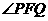 为钝角,求直线
为钝角,求直线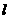 的斜率
的斜率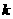 的取值范围.
的取值范围.
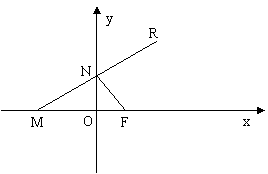 (2)(文)过
(2)(文)过 作直线
作直线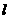 交轨迹
交轨迹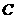 于
于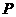 、
、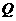 两点,求
两点,求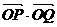 的值.
的值.
21.(本题满分16分)本题共有3个小题,第1小题满分4
分,第2小题满分5分 , 第3小题满分7分.
用 表示数列
表示数列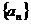 从第
从第 项到第
项到第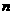 项(共
项(共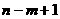 项)之和.
项)之和.
(1)在递增数列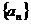 中,
中,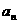 与
与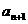 是关于
是关于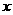 的方程
的方程 (
(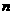 为正整数)的两个根.求
为正整数)的两个根.求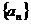 的通项公式并证明
的通项公式并证明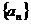 是等差数列;
是等差数列;
(2)对(1)中的数列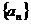 ,判断数列
,判断数列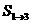 ,
,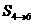 ,
,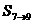 ,…,
,…,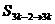 的类型;
的类型;
(3)(理)对一般的首项为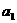 ,公差为
,公差为 的等差数列,提出与(2)类似的问题,你可以得到怎样的结论,证明你的结论.
的等差数列,提出与(2)类似的问题,你可以得到怎样的结论,证明你的结论.
(3)(文)对(1)中的数列作进一步研究,提出与(2)类似的问题,你可以得到怎样的结论,证明你的结论.
19.(本题满分14分)本题共有2个小题,第1小题满分6
分,第2小题满分8分.
 某种商品在
某种商品在 天内每件的销售价格
天内每件的销售价格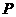 (元)与时间
(元)与时间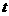 (天)的函数关系用下图中的两条线段表示;该商品在
(天)的函数关系用下图中的两条线段表示;该商品在 天内的日销售量
天内的日销售量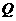 (件)与时间
(件)与时间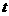 (天)之间的关系如下表所示:
(天)之间的关系如下表所示:
第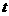 天 天 |
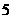 |
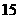 |
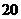 |
 |
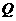 (件) (件) |
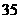 |
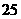 |
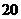 |
 |
(1)根据提供的图象,写出该种商品每件的
销售价格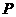 与时间
与时间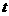 的函数关系式,并根据表中数
的函数关系式,并根据表中数
据确定日销售量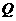 与时间
与时间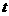 的一个函数式;
的一个函数式;
(2)用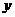 表示该商品的日销售金额,写出
表示该商品的日销售金额,写出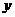
关于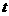 的函数关系式,求该商品的日销售金额的最
的函数关系式,求该商品的日销售金额的最
大值,并指出日销售金额最大的一天是 天中的第几天?
天中的第几天?
18.(本题满分12分)
(理)在四面体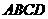 中,
中,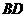 、
、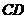 、
、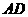 两两互相垂直,且
两两互相垂直,且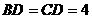 ,
,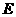 是
是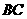 中点,异面直线
中点,异面直线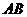 与
与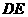 所成角的大小是
所成角的大小是 ,求四面体
,求四面体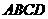 的体积.
的体积.
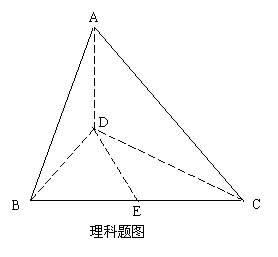
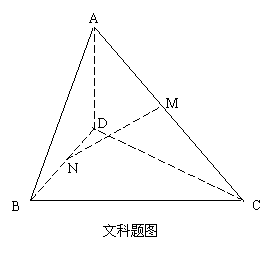 (文)如图,在四面体
(文)如图,在四面体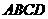 中,
中,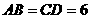 ,异面直线
,异面直线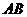 、
、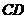 所成角的大小是
所成角的大小是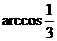 ,
,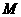 、
、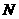 分别是
分别是 、
、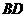 的中点.求线段
的中点.求线段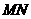 的长.
的长.
17.(本题满分12分)
已知复数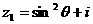 ,
,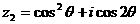 ,其中
,其中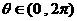 .设
.设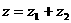 ,且复数
,且复数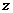 在复平面上对应的点
在复平面上对应的点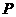 在直线
在直线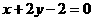 上,求
上,求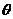 的值所组成的集合.
的值所组成的集合.
16.(理)一个机器人每一秒钟前进或后退一步,程序设计师让机器人以前进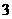 步,再
步,再
后退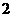 步的规律移动.如果将机器人放在数轴的原点,面向正的方向,以
步的规律移动.如果将机器人放在数轴的原点,面向正的方向,以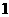 步的距
步的距
离为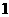 个单位长度.令
个单位长度.令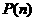 表示第
表示第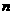 秒时机器人所在位置的坐标,且记
秒时机器人所在位置的坐标,且记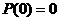 .
.
则下列结论中错误的是………………………………………………………………( )
(A)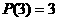 (B)
(B)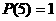 (C)
(C)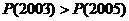 (D)
(D)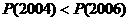
(文)设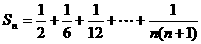 ,且
,且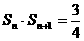 ,则
,则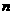 的值是…………( )
的值是…………( )
(A) 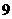 (B)
(B)
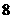 (C)
(C)
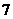 (D)
(D)
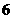
15.(理)已知函数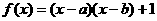 ,且
,且 、
、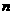 是方程
是方程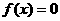 的两根,则实数
的两根,则实数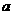 、
、
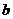 、
、 、
、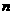 的大小关系可能是…………………………………………………………( )
的大小关系可能是…………………………………………………………( )
(A) 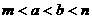 (B)
(B) 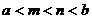 (C)
(C) 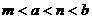 (D)
(D) 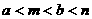
(文)函数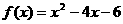 的定义域为
的定义域为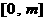 ,值域为
,值域为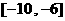 ,则
,则 的取值范
的取值范
围是……………………………………………………………………………………( )
(A) 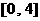 (B)
(B) 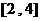 (C)
(C) 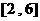 (D)
(D) 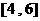
14.在实数集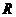 上定义运算
上定义运算 :
: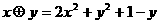 ,则满足
,则满足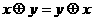 的实数对
的实数对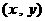 在平面直角坐标系内对应点的轨迹是……………………………………( )
在平面直角坐标系内对应点的轨迹是……………………………………( )
(A) 一个圆 (B) 双曲线 (C) 一条直线 (D) 两条直线
13.已知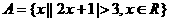 ,
,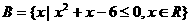 ,则
,则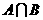 为…( )
为…( )
(A) 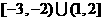 (B)
(B) 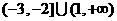 (C)
(C)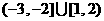 (D)
(D)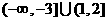
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com